考慮便乘的地鐵乘務任務配對的約束優化模型研究

馬 亮，徐曉英

(1. 西南交通大學 信息科學與技術學院，四川 成都 610031；2. 中國鐵路西安局集團有限公司，陜西 西安 710608)

地鐵車輛基地(包括車輛段和停車場)主要作業任務為檢修、行車和乘務，行車依據檢修需求和車輛狀態為運行車次分配車輛，乘務管理為行車提供司乘保障。乘務管理的核心是依據乘務制度編制乘務排班計劃，實現乘務任務、司機出/退勤、司機輪休、司機用餐和司機工作量的管理，保障正線行車效率和乘務人員身心健康，達到減員增效的目的。

乘務排班計劃主要包括：乘務任務配對(Crew Scheduling)和乘務任務指派(Crew Rostering)兩個問題。其中，乘務任務配對是指依據乘務作業限制，將給定的列車運行計劃配對成若干乘務任務；乘務任務指派是指依據乘務班組和輪班制度將乘務任務配對結果指派給具體的司乘人員，形成司乘人員一天的值乘計劃。一般情況下，司乘人員駕駛列車出勤或者值乘，若司乘人員不在出勤點或者退勤點，就需要像乘客一樣便乘其他列車至出勤點或者退勤點。因此，乘務任務可以分為值乘任務(Crew Tasks)和便乘任務(Passenger Tasks)。便乘是指多組司乘人員同時值乘一個列車，其中1組司乘人員擔任司機，其他組司乘人員以乘客身份便乘前往目的地出勤或者退勤，即部分司乘人員只能在非出勤點開始乘務任務或者在非退勤點結束乘務任務。

國外針對鐵路司乘任務優化問題：文獻[1]考慮了司乘人員可以乘坐其他交通工具便乘出勤和對原有乘務任務修改最少，建立了荷蘭鐵路司乘人員重新調度的集合覆蓋(Set Covering, SC)模型，但是重新調度的計算時間較長；文獻[2]研究了鐵路貨物夜間運輸的乘務任務公平調度問題，以乘務任務調度成本最小、不受歡迎的乘務任務最少和不受歡迎乘務任務分配均衡為目標，建立了歐洲鐵路運輸公司乘務調度的SC模型，并設計了最短路徑和線性規劃松弛的混合算法；文獻[3]重點考慮了任務調度和司乘人員薪酬的均衡性，建立了智利工礦企業工藝鐵路的乘務任務調度的0-1整數規劃模型，但是改進的局部啟發式搜索算法求解耗時達幾個小時。由于國外法規制度和鐵路值乘制度與國內不同，因此需要研究符合我國國情的乘務任務配對優化問題。

針對我國鐵路乘務排班計劃優化問題：文獻[4]建立了臺灣地區鐵路客運乘務排班計劃的綜合0-1優化模型，并使用深度優先回溯搜索算法(DFS)求解，算例表明綜合模型比分解模型的解更優；文獻[5]以總交路時間最小和各乘務交路間均衡最大為目標，建立乘務交路優化的多旅行商模型，算例驗證表明改進蟻群算法比遺傳算法求解效果好；文獻[6] 建立了客運專線乘務交路計劃的SC模型，但是分支定價算法求得初始解的時間較長，算法的可信度不高；文獻[7]以乘務人員效率最高為目標，建立了乘務交路計劃的SC模型，但是模型中未考慮便乘情況、實際的乘務制度、勞動規章等關鍵因素。

相對于國鐵，地鐵具有乘務任務段相對確定、行車密度大、交路相對簡單、有多個乘務輪換點等特點。目前，現場絕大多數司乘派班調度員借助辦公軟件人工編制司乘排班計劃，司乘班組的工作效率得不到保證，需要研究地鐵乘務排班優化問題。文獻[8-10]以總費用最少為目標建立雙層整數規劃模型，并分別使用最短路、最小費用最大流、Hungarian、禁忌搜索、Dijkstra和離散粒子群等算法求解；文獻[11]探討了乘務排班和值乘方式，比較得出輪乘制比包乘制更節省費用；文獻[12-13]建立乘務任務配對的SC和集合分解(Set Partition, SP)模型，并借鑒列生成思想設計混合算法求解；文獻[14]建立乘務任務分配的0-1整數規劃模型，設計了列生成和跟隨分支策略的混合算法，但是應該考慮更長期乘務任務的均衡性；文獻[15]針對啟發式算法或者列生成算法求解復雜、難于實際應用等問題，以列生成算法為框架，將整個優化問題分解為SP主規劃模型和加權網絡最短路徑的子規劃模型兩部分，但是在實際應用時成本函數中的權值較難確定。

現有研究主要是建立乘務排班計劃的0-1規劃模型，再使用解析算法和啟發式算法求解，取得了大量的理論成果，但是與投入實際應用之間存有一定的差距。關鍵問題是所建模型是結構化的數學表達式，難于使用程序語言直接表示；而且針對不同的算例，算法性能的波動較大。同時，部分模型存在不深入和值得商榷的地方，譬如：乘務任務與乘務任務段之間的關系定量描述不精確、各約束沒有分情況討論等。本文使用約束程序(Constraint Programming, CP)[16-17]理論研究便乘情況下的乘務任務配對問題，建立約束優化(Constraint Optimization, CO)[17]模型，并依據模型特點使用弧邊界相容的約束傳播(Constraint Propagation, CPr)[17]算法化簡模型，最后使用CPr和啟發式回溯的混合算法求解模型。

1 地鐵乘務任務配對問題

乘務任務配對指將給定的列車運行計劃配對成若干乘務任務，每個乘務任務由1個乘務班組1天完成，因此，列車運行圖是乘務任務配對的基礎。列車運行圖中縱軸表示所有停靠車站，這些車站按照用途可以分為兩類：一類是普通乘客換乘點；另一類是乘務分割點。其中乘務分割點是乘務員進行出/退勤、輪換休息和用餐的站點。移除列車運行圖中的乘客換乘點得到只保留乘務分割點的乘務運行線集合為

G={Gi,1≤i≤NG}

式中：Gi(1≤i≤NG)為第i條乘務運行線集合；NG為總的運行線數量。

將每一條乘務運行線Gi上相鄰乘務分割點之間的運行任務片段稱為乘務任務段，則第i條乘務運行線Gi的第l個乘務任務段為

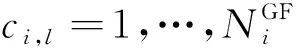
乘務任務段劃分示意圖見圖1。

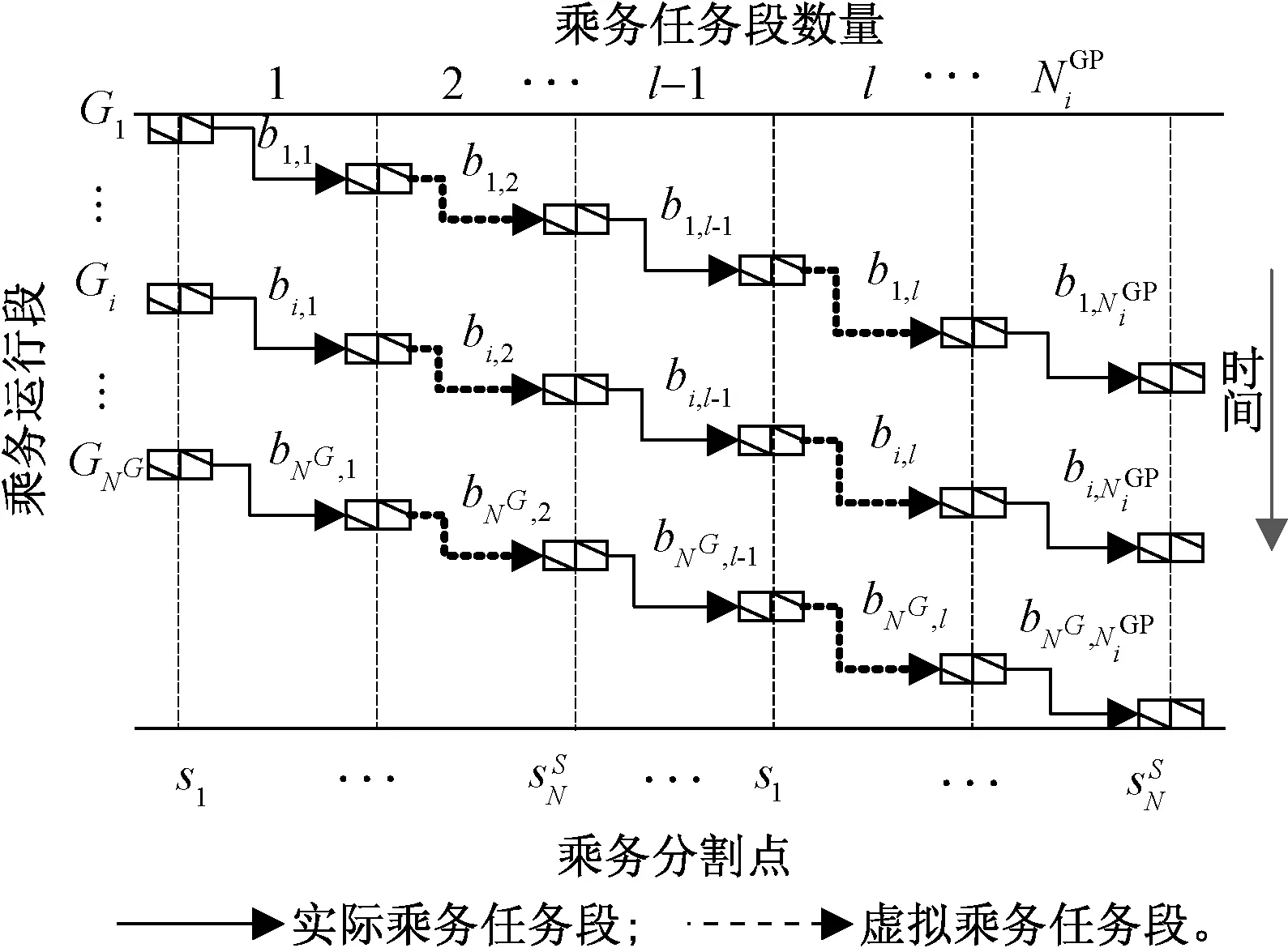
圖1 運行線的乘務任務段劃分示意圖

為了論述乘務任務配對問題，定義變量見表1.

表1 乘務任務配對問題變量及說明

一個乘務任務是指司乘人員從出勤點開始，值乘若干乘務任務段并最終從退勤點結束的全過程[5]，由若干乘務任務段按照一定的乘務規則鏈接而成。因此，乘務任務段是乘務任務配對的基本單元，其數量與每日列車運行次數、乘務分割點的分布密切相關，并直接決定了乘務任務配對問題的復雜度。乘務任務段之間的樹形鏈接關系見圖2。

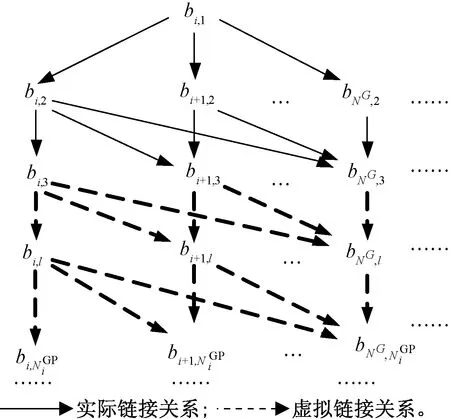
圖2 乘務任務段鏈接關系的樹形結構示意圖

2 地鐵乘務任務配對的約束優化模型

CO模型記為四元組(X,D,C,F)，其中：X為變量集合；D為變量論域集合；C為約束集合；F為目標函數集合[17]。令某一變量x∈X取值表示為x←v∈D(x)，則CO求得最優解S={(x←v)|?x∈X,v∈D(x)}是指對于任意約束?c∈C滿足相容性檢查c(S)=1，同時使得任意目標函數?f∈F達到最優。CO的約束是由變量或者變量表達式之間通過邏輯謂詞(與“∧”、或“∨”、非“！”、蘊含“=>”等)聯接形成的關系[17]。乘務任務配對受到地點、時間、工作強度等限制，而且各約束之間存在較強的邏輯關系，使用CO直接建立考慮便乘的乘務任務配對優化模型(Constrained Optimization Model for Crew Pairing, COCP)。

2.1 常量定義

表2 常量變量及說明

2.2 變量定義

每一個乘務任務段可以視為最小的乘務任務，理論上最多的乘務任務數量等于NB，令以bm為開始任務區段的乘務任務Bm為變量，則定義變量見表3。

表3 任務區段的乘務任務Bm為變量及說明

依據上述定義，乘務任務的結構見圖3。

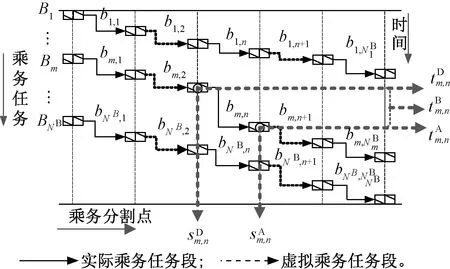
圖3 乘務任務結構示意圖

2.3 目標函數

為了降低地鐵運營成本和提高乘務人員的工作效率，乘務任務配對優化的主要目標是在允許便乘的情況下乘務任務數量最少，表示為

(1)

2.4 約束條件

乘務任務配對需要滿足乘務人員總的工作量、乘務人員連續工作量、乘務任務的班次劃分、出/退勤地點、輪休時間和地點、用餐時間和地點、乘務任務段完整性等限制。

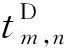
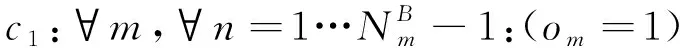
(2)

(2)1個乘務任務內相鄰的乘務任務段之間，前1個乘務任務段的到達地點是后1個乘務任務段的出發地點，即乘務任務內的乘務任務段之間需要滿足鏈接關系

(3)

(3)如果某一個乘務任務的開始車站不是出勤點或者結束車站不是退勤點，那么此乘務任務段為便乘的乘務任務段

c3:?m:(om=1∧wm=1)

(4)

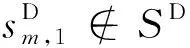
(4)在最終形成的乘務任務方案應該包括所有的乘務任務段，而且1個乘務任務段只屬于1個乘務任務。則乘務任務段全覆蓋和唯一性約束為

(5)

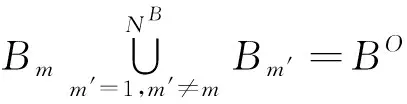
(5)為了保證乘務人員之間的工作量均衡，每一個乘務任務需要滿足所屬班次總的工作量約束為

(6)

(6)所形成的乘務任務Bm中所有的乘務任務段要么沒有特殊的需求，要么滿足退勤、輪休、用餐中的1個需求，則乘務任務段特殊需求唯一性約束為

c6:?m,?n:(om=1)?(dm,n=rm,n+hm,n+em,n)

(7)

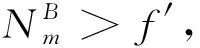
(7)為了保證各司乘人員工作量均衡和避免疲勞駕駛，乘務任務內總的工作時間不能超過上限，否則，需要退勤，則總的工作量約束為

(8)

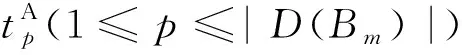
式(8)表示當乘務任務Bm滿足其他約束的論域D(Bm)不為空時，但是其中任意乘務任務段加入到Bm中均會超過總的工作時間的上限，則需要退勤。

(8)為了保證司乘人員的身心健康，司乘人員連續工作時間不能超過持續工作時間上限，如果超過，則需要輪換休息，則連續工作量約束為

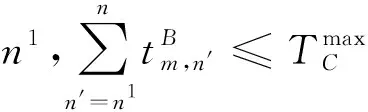
(9)一般情況下乘務任務分為早、白、夜3班，通過乘務任務的開始和結束時間來區分乘務任務所屬班次，則乘務任務班次劃分約束為

c9:?m,?u∈ST:(om=1∧um=u)

(11)

(10)早班中的非便乘出勤的乘務任務直接從車輛基地駕駛出勤

(12)

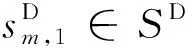
(11)晚班中的不是便乘退勤的乘務任務直接駕駛到車輛基地退勤：

(13)

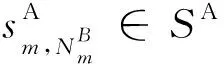
(12)為了保證司乘人員的身心健康，乘務人員連續駕駛一段時間之后需要在輪換點休息，則乘務任務的輪換休息持續時間和地點約束為

(14)

(13)乘務人員連續駕駛一段時間之后需要在規定地點和時間范圍內用餐，而且需要保證用餐時間，則乘務任務的用餐持續時間和地點約束包括是否用餐約束和用餐時間、地點約束為

(15)

COCP模型為單目標的約束優化模型，每一個乘務任務的確定問題為大規模的NP-Hard問題，首先通過約束傳播算法剔除解空間中不可能成為解的那部分變量取值，縮小解空間，減少無效搜索。但是約束傳播算法缺乏完備性，同時基本回溯算法(Backtracking Algorithms, BT)未使用已實例化變量進行相容性檢查避免未來沖突，求解時間較長，因此，設計了約束傳播和啟發式回溯(Heuristic BT, HBT)的混合搜索算法(CPr-HBT)快速求解模型。

3 乘務任務配對的混合搜索算法

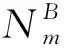
(16)

混合搜索算法(CPr-HBT)步驟如下：

Step1如果未達到總的求解時間或者迭代次數，轉Step2，否則，返回使得f最小的解B={Bm}。

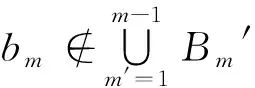
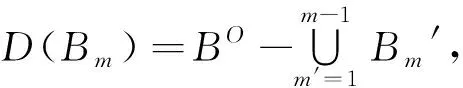
Step4初始約束傳播約減D(Bm)。在使用啟發式回溯算法求解乘務任務Bm前，使用約束傳播算法對乘務任務Bm的論域D(Bm)進行約減，轉Step5。

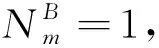
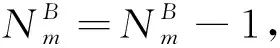
4 算例分析

4.1 算例求解

某地鐵線路的站點設置見圖4，共有北郊、軍區和太平3個乘務分割點。其中北郊為車輛段，北郊和軍區為出/退勤點、軍區和太平為乘務輪換休息點、軍區為用餐點。

某日此地鐵線路有101～120共20個運行車次，其中101～118車次之間的間隔為10 min、單向運行次數都為18、在同一單向運行中相同乘務分割點輪換休息時間相同，119和120車次之間的間隔為5 min、單向運行次數都為4、在同一單向運行中相同乘務分割點輪換休息時間相同。不同車次相同運行區間的運行時間相同，其中北郊和軍區之間雙向運行時間均為10 min，軍區和太平之間雙向運行時間均為45 min，則依據運行圖和乘務分割點劃分得到101和119車次的乘務任務段見表3，表格中b1,l(1≤l≤20)為101車次的乘務任務段，b19,l(1≤l≤6)為119車次的乘務任務段，102～118車次的乘務任務段劃分類似于101車次的乘務任務段劃分，120車次的乘務任務段劃分類似于119車次的乘務任務段劃分。模型中其他參數見表4。

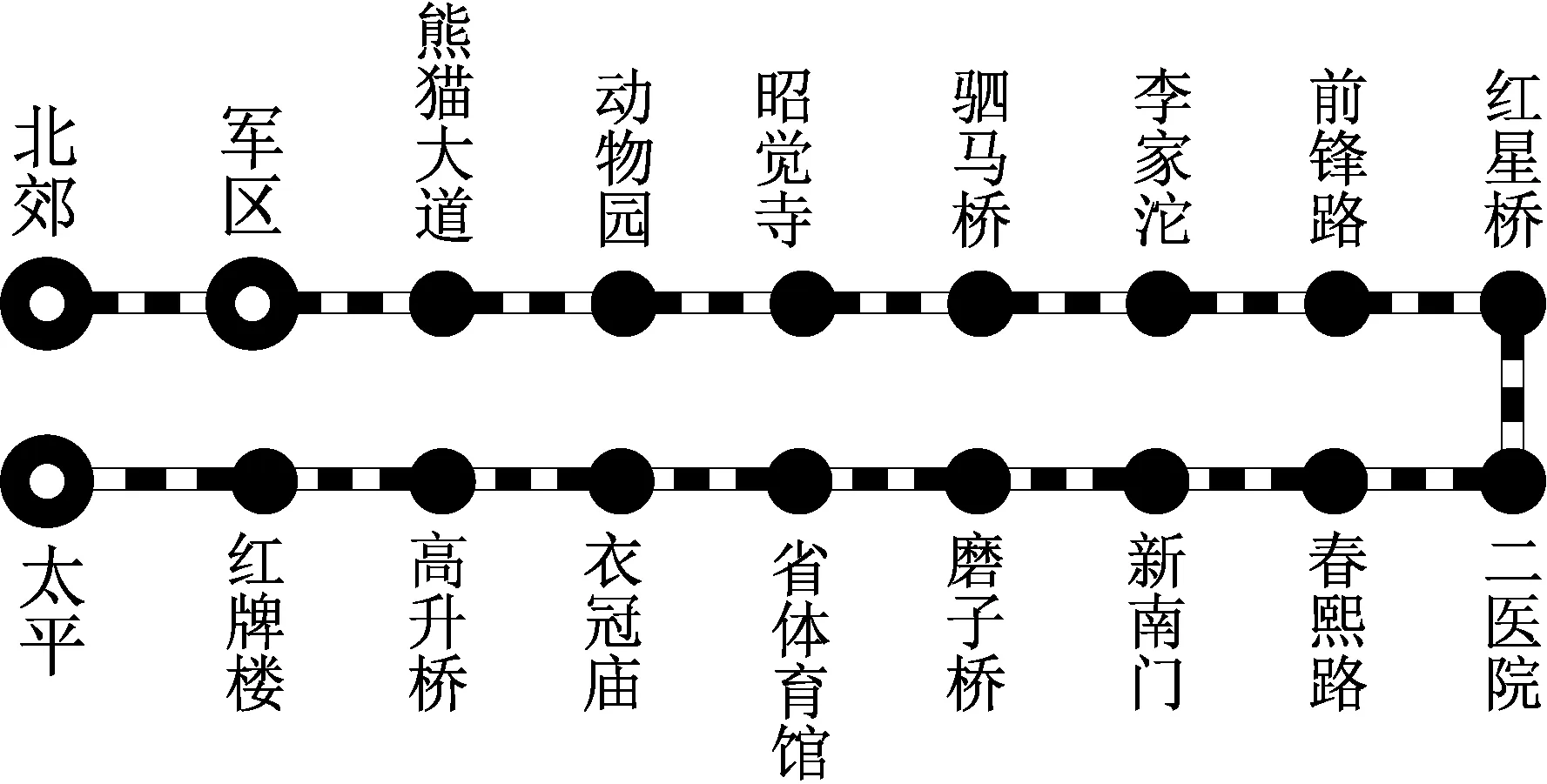
圖4 某地鐵線路的站點設置示意圖

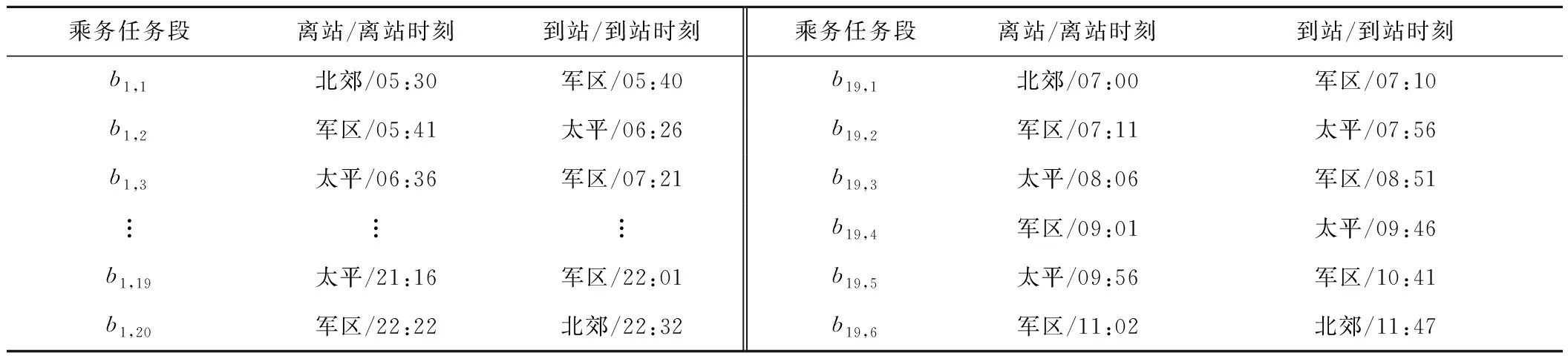
表3 某地鐵線路某日乘務任務段

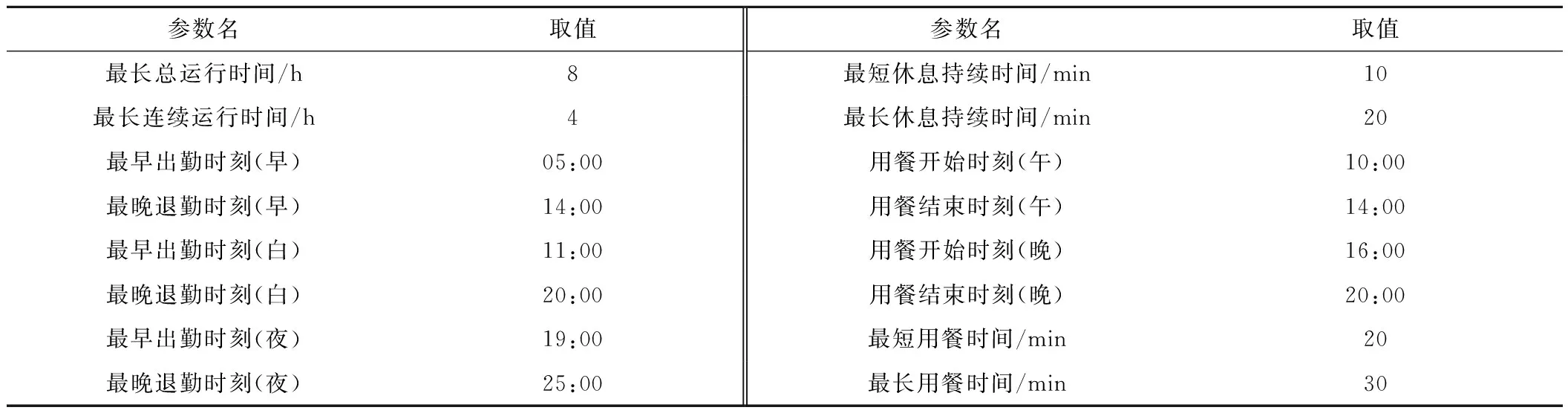
表4 某地鐵線路乘務計劃參數表

本算例的乘務任務段總數為372，變量有1 442個，約束的數量級為百萬，在Inter Core i3-2 310 M 2.1 GHz & DRAM 2 G & Windows XP &.NET Framework 4.5環境下的PC機上運行本模型及算法，根據現場需求設置算法總的求解時間上限為200 s或者總的迭代次數上限為20 000次。CPr-HBT算法的求解過程見圖5，乘務任務配對結果見表5、圖6。從圖5中可知求得較優解至少需要迭代5 600次，總的花費時間為56.35 s，產生了56個乘務任務，在這些乘務任務中需要進行31次便乘，乘務員之間工作時間最多相差了310 min。

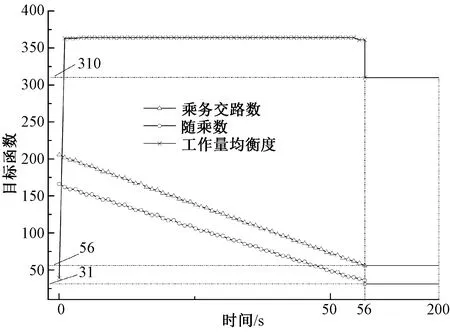
圖5 CPr-HBT混合算法的求解過程

圖6中早班、白班和夜班各有兩種情況。早01～早18的乘務任務為?i=1…18:{bi,l|l=1…9}，早19～早20的乘務任務為?i=19…20:{bi,l|l=1…6}；白01～白09的乘務任務為?i=1…9:{bi,l|l=10…16}，白10～白18的乘務任務為?i=10…18:{bi,l|l=10…15}；夜01～夜09的乘務任務為?i=10…18:{bi,l|l=16…20}，夜10～夜18的乘務任務為?i=1…9:{bi,l|l=17…20}。

從圖5中的算法求解過程可以看出：目標函數值是單調遞增或者遞減的，較少出現震蕩，說明通過約束傳播技術保證了最優解的求解效率和概率。通過圖6可得：乘務任務覆蓋了表1中所有的乘務任務段，所有的乘務任務滿足所有約束條件，而且滿足現場的對計劃編制的時效性需求。

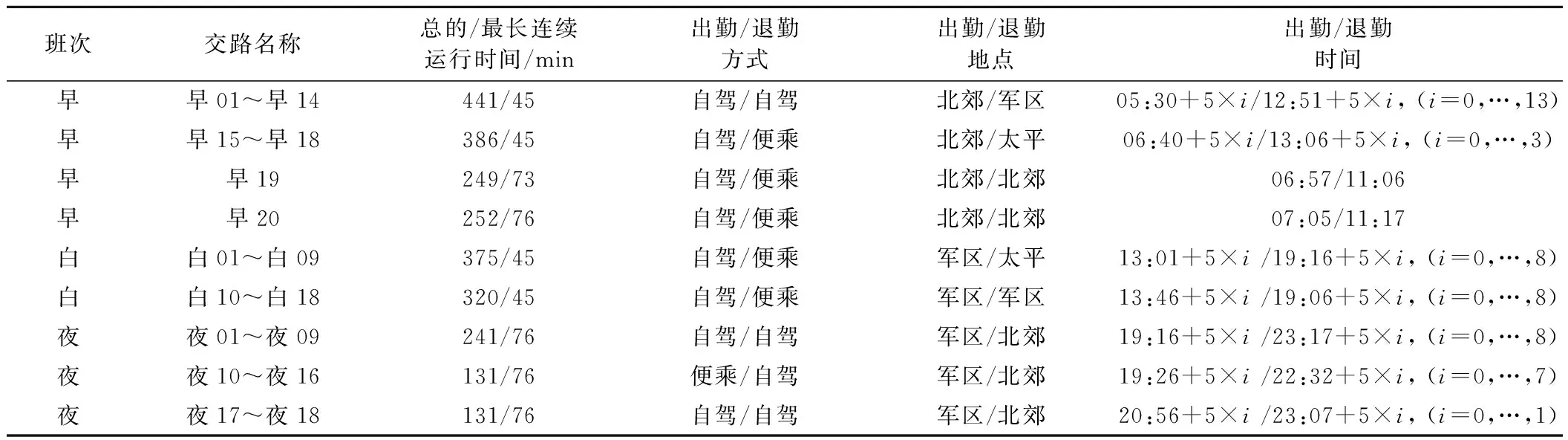
表5 乘務任務配對結果

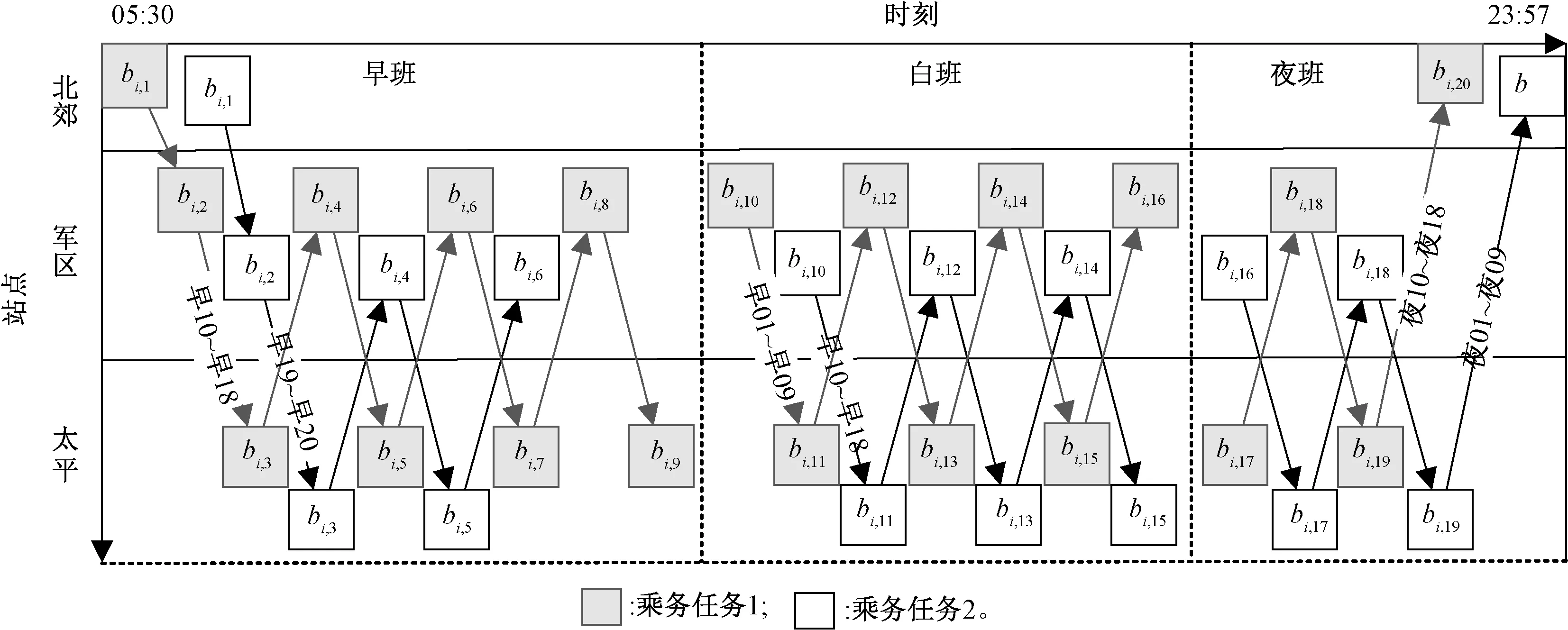
圖6 乘務任務配對結果示意圖

4.2 算法比較

為了驗證本算法的求解效率，在不改變其他參數的情況下，使用文獻[4]中不帶約束傳播的深度優先回溯算法(DFS)求解本模型，求解過程見圖7。

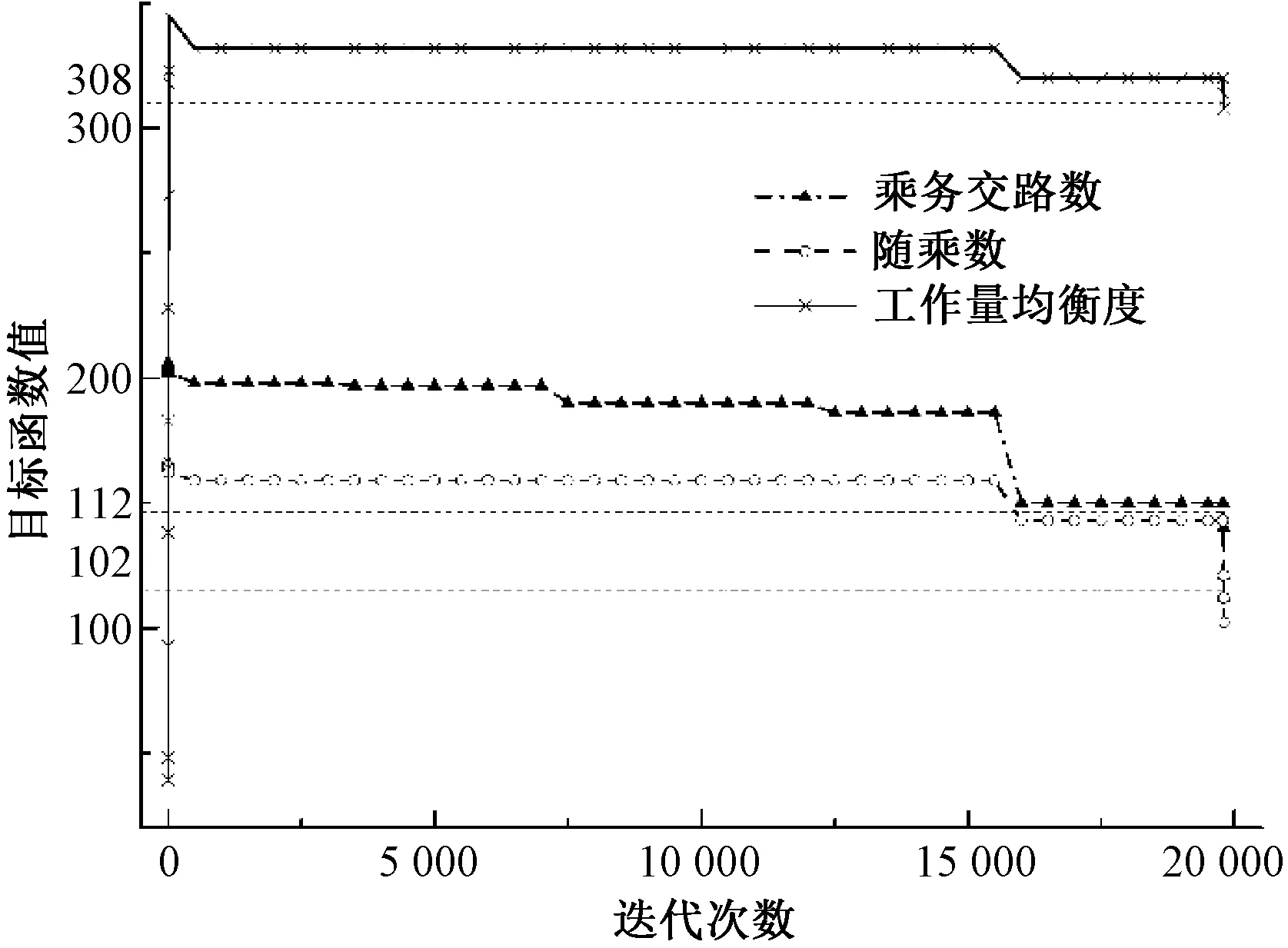
圖7 使用DFS算法目標函數的求解過程

DFS達到迭代上限20 000次時，形成的乘務任務數為112個乘務任務，有102次便乘，乘務員之間總的工作時間相差了308 min。因此，不帶約束傳播的改進回溯算法的求解效率和求解質量都比本文算法要低，驗證了本混合算法的高效性。

5 結論

本文綜合考慮了乘務人員的工作效率、工作量的均衡性和乘務員便乘等因素，建立了考慮便乘的乘務任務配對的約束優化模型。之后設計了約束傳播與啟發式回溯的混合算法求解了模型；最后通過現場實際算例驗證結果表明：與現場和其他算法相比，本論文的模型和算法優勢明顯。本論文提出的使用約束程序方法對于考慮便乘的地鐵乘務任務配對優化問題是可行的，模型符合現場實際業務需求，保證了排班計劃的適用性；本混合算法求解效率和穩定性較高，滿足現場對排班計劃編制的實時性要求。本論文提出的模型和算法已經成功應用于地鐵車輛基地綜合自動化系統中，結合乘務任務指派優化方法，共同輔助司乘派班調度工作，降低了派班調度員的工作強度，提高了作業效率。