對一道2021年八省市聯考題的反思與結論拓展*

湖北省恩施州教育科學研究院(445000) 周 威

一、試題呈現與問題反思

例1(2021年八省市聯考數學第21 題) 雙曲線= 1(a ＞0,b ＞0) 的左頂點為A, 右焦點為F,動點B在C上.當BF⊥AF時,|BF|=|AF|.

(1)求C的離心率;

(2)若B在第一象限,證明: ∠BFA=2∠BAF.

此題題干簡潔,要證明的結論也十分簡約,給人第一印象就是“清爽”簡單.實際上,本題解題思路開闊,解法也不唯一.第(1)問答案為離心率e=2;第(2)問對學生來說入手容易,重點考查化歸轉化思想,考查學生對“斜率”與“傾斜角”的轉換關系, 通過正切的倍角公式證明角與角之間的關系,落腳于考查學生邏輯推理、直觀想象素養,與傳統的“直線代入圓錐曲線方程”數學運算有一定的區別,從而難度上有所下降.毫無疑問,第(2)問中的關系式∠BFA= 2∠BAF是在離心率e= 2 時才成立,解題過程中要抓住其數學本質即直線BA,BF的特殊斜率關系tan ∠BFA=tan 2∠BAF.

那么,在一般的雙曲線中,甚至在一般的圓錐曲線中,直線BA,BF的斜率關系是怎樣的? 數學教師若能從這個“一般與特殊”的角度,運用歸納與演繹推理,那么對問題的認識無疑是更深入更全面的.

二、結論拓展

結論1雙曲線= 1(a ＞0,b ＞0)的左頂點為A,右焦點為F,動點B在C上,記C的離心率為e,設直線BA的斜率為k1(k1/=0),直線BF斜率為k2(k2/=0),則k2=

證明因為A(-a,0),F(ea,0),設(0＜θ ＜2π,θ /=π),則

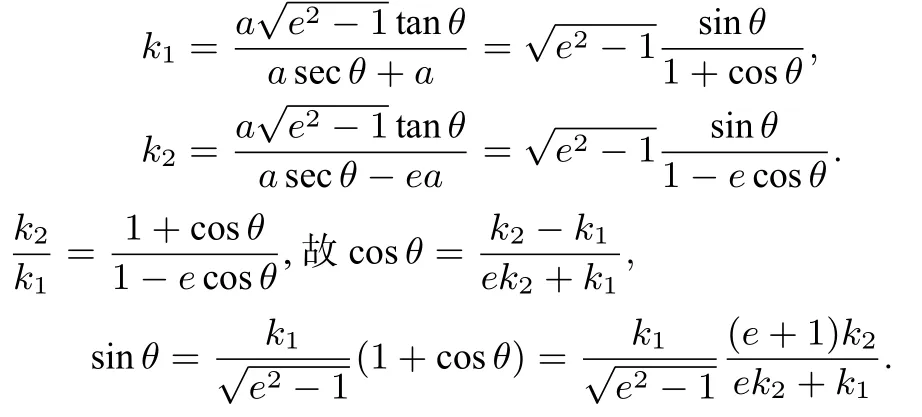
所以

即

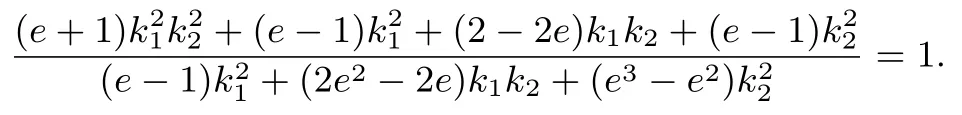
化簡得

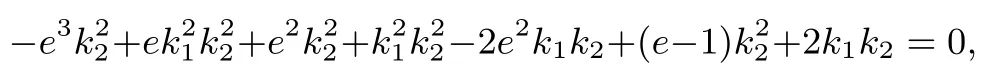
即

由于k2/=0,化簡可得

特別地, 當e= 2 時,k2=而k2=-tan ∠BFA, 從而有例1 中要證明的等式關系.另外, 此結論對橢圓也成立,拋物線情形類似.

結論2橢圓C:= 1(a ＞b ＞0)的左頂點為A,右焦點為F,動點B在C上,記C的離心率為e,設直線BA的斜率為k1(k1/= 0), 直線BF斜率為k2(k2/= 0), 則

證明因為A(-a,0),F(ea,0),設(0＜θ ＜2π,θ /=π),則

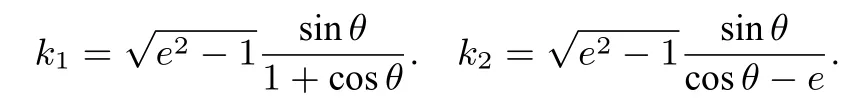
所以

即

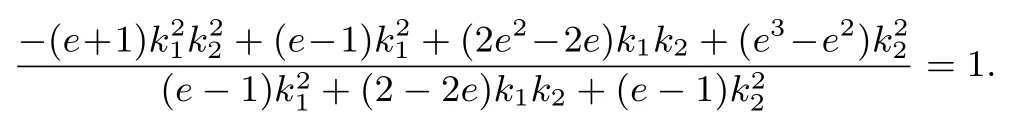
移項有

即

由于k2/=0,化簡可得

結論3拋物線C:y2= 2px(p ＞0)的頂點為A,焦點為F,動點B在C上,記直線BA的斜率為k1(k1/= 0),直線BF斜率為k2(k2/=0),則k2=

證明因為A(0,0),設B(2pt2,2pt)(t /= 0),

三、結論的應用舉例

例2已知橢圓= 1(a ＞b ＞0)經過點設橢圓左頂點為A,右焦點為F,右準線與x軸交于點M,且F為線段AM的中點.

(1)求橢圓C的標準方程;

(2)若過點A的直線l與橢圓C相交于令一點P(P在x軸上方),直線PF與橢圓C相交于另一點Q,且直線l與OQ垂直,求直線PQ的斜率.

解析(1)

(2) 由(1) 得橢圓離心率e=設直線l斜率為k1(k1＞0), 直線PQ斜率為k2, 則OQ的斜率為由結論2 可得k2=直線OQ方程為y=PQ方程為y=聯立可得因為Q在橢圓上,解得k1=從而k2=

點評本題考查橢圓與直線位置關系、直線斜率的求法,當然可以從通性通法的角度將直線代入橢圓方程,利用韋達定理進行求解.而基于探究結論的解答,一定程度上體現數學探究在解題教學中的重要性.

例3過橢圓C:= 1(a ＞b ＞0)的左頂點A且斜率為的直線交橢圓C于另一點B,橢圓的右焦點為F,連接BF,設BF的斜率為k,若k ＜-1,則橢圓離心率的取值范圍是____.

解析設橢圓離心率為e, 由結論2 可得,k=因為k ＜-1,1-e ＞0,所以

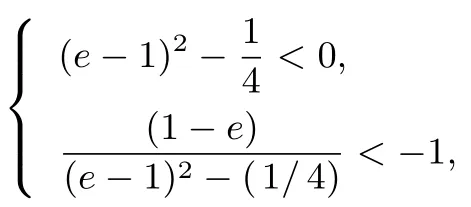
由(e-1)2-得e2-3e+＞0,從而e ＜或e ＞故

點評考查了橢圓與直線的位置關系,基于探究結論,從直線的斜率和橢圓的離心率的關系進行命題創設.

復習備考中很有必要立足基礎素材,從試題隱性要素的角度抓住數學問題本質,實現對試題知識點的拓展、發散,以及對相關知識點的重組和整合,基于教材和高考導向進行試題改編,引導學生發現、提出問題,試圖讓學生抓住同類數學問題的本質.