核酸檢測背后的數(shù)學原理

福建省石獅市第三中學(362700) 李 榕

新冠疫情爆發(fā)以來,我國在武漢、北京、新疆等地開展全員新冠病毒核酸檢測篩查.面對數(shù)量巨大的檢測樣本我們采用了混合檢測方式,這樣的方式是否有效合理? 本文以數(shù)學建模的方式探究核酸檢測過程中的數(shù)學問題,從而解釋核酸檢測背后的數(shù)學原理.

關鍵字 核酸檢測;混合檢測;均值不等式;二項分布

一、問題的提出

2020年5月11日武漢市下發(fā)《關于開展全市新冠病毒核酸篩查的緊急通知》,要求在10 天之內(nèi),對全武漢人員做一次核酸檢測,徹底摸清武漢市的人員感染新型肺炎病毒的詳細情況.

在新冠肺炎疫情防控期間,利用核酸檢測出武漢市存在的確診病例對早日戰(zhàn)勝疫情來說至關重要.然而核酸檢測確診病例最快的話也需要幾個小時,因此檢測策略的效率將直接影響疫情的防空和確診病人的救治.面對我國這樣巨大的檢測人數(shù)壓力以及龐大的公共衛(wèi)生經(jīng)濟資源的壓力,去探究一種有效的解決途徑勢在必行.

2020年6月2日,湖北省新冠病毒肺炎疫情防控工作指揮部召開新聞發(fā)布會,介紹武漢市在十天內(nèi)集中核酸檢測排查結果,如下表[1]:

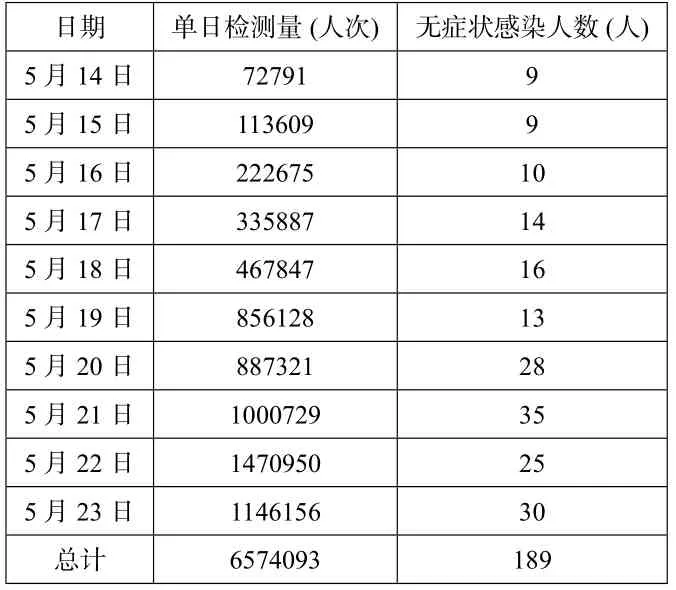
武漢市新冠病毒核酸檢測“十天大會戰(zhàn)”情況

為什么說657.4 萬的檢測試劑數(shù)量完成了武漢約1000萬人全員排查的呢? 面對大于1 千萬人數(shù)的檢測需求,武漢一天需要完成超百萬的檢測量,這樣的艱難目標到底如何去實現(xiàn)? 其中核酸檢測的背后數(shù)學原理是什么呢?

二、數(shù)學模型

(一)模型假設:

1.新冠病毒核酸檢測試劑的判斷正確率為100%.

2.新冠病毒核酸檢測試劑同樣可以正確檢測出混合樣本,當混合樣本的人均為陰性時則顯現(xiàn)陰性特性,否則顯示陽性特征.

3.假設每個人的取樣足夠多,且分組之后不影響最終檢測結果.

4.假設武漢各地區(qū)感染情況是均勻分布的,且病毒總體感染率為p

(二)數(shù)學記號:

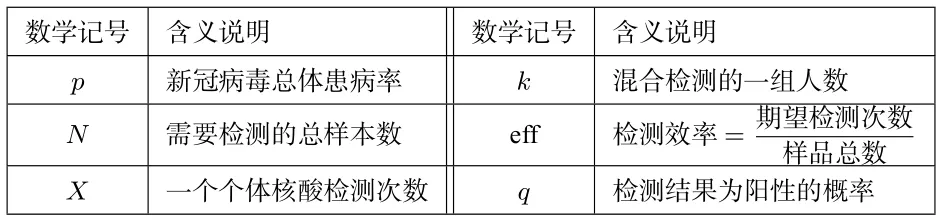
數(shù)學記號含義說明數(shù)學記號含義說明________________p 新冠病毒總體患病率k 混合檢測的一組人數(shù)N 需要檢測的總樣本數(shù)eff 檢測效率= 期望檢測次數(shù)樣品總數(shù)X 一個個體核酸檢測次數(shù)q 檢測結果為陽性的概率____

(三)模型建立與求解

1.初步探究問題

假設武漢各地區(qū)感染情況是均勻分布的,現(xiàn)對某社區(qū)進行新冠病毒核酸檢測,全員100 人采集樣本后,每20 個樣本為一組,每組內(nèi)的20 個樣本混合起來,這樣共得到5 組樣本.若某個組的混合樣本檢測為陽性,則對這組的20 人再去進行逐一檢測.記該社區(qū)檢測總次數(shù)為η,且各組之間相互獨立.求一個混合樣本為陽性的概率q及其該社區(qū)檢測總次數(shù)η分布列和期望.

2.初步探究結論

共需要檢測多少次? 寫出所有可能的次數(shù).

·5 組都是陰性,則共需要5 次檢測;

·1 組是陽性,4 組陰性,則共需要5+20 次檢測;

·2 組是陽性,3 組陰性,則共需要5+20+20 次檢測;

·3 組是陽性,2 組陰性,則共需要5+20+20+20 次檢測;

·4 組是陽性,1 組陰性,則共需要5+20+20+20+20 次檢測;

·5組是陽性,0 組陰性,則共需要5+20+20+20+20+20 次檢測.

可得一組混合樣本檢測為陰性的概率為(1-p)20,陽性的概率為q=1-(1-p)20,η可能的取值為5,25,45,65,85,105.概率分布列圖如下:

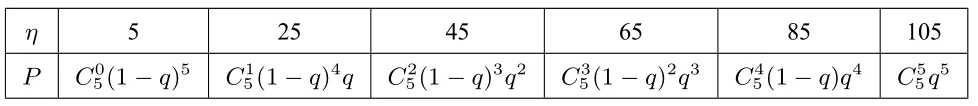
η 5 25 45 65 85 105 P C05(1-q)5 C15(1-q)4q C25(1-q)3q2 C35(1-q)2q3 C45(1-q)q4 C55q5

假設共有Y組檢測結果為陽性,則Y ～B(5,q).因此E(Y)=5q.又由于隨機變量η與Y的關系可得:

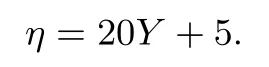
所以社區(qū)檢測總次數(shù)為η的數(shù)學期望為:

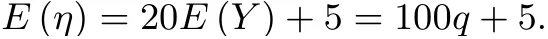
3.再探究問題

4.再探究結論

易知,單次核酸檢測效率為1,即每個個體所需的檢測次數(shù)為1 次,一般來說個體平均需要檢測的次數(shù)往往低于1.所以只需要求出每個個體的核酸檢測次數(shù)X的數(shù)學期望,如果數(shù)學期望小于1,說明每個個體的檢測次數(shù)平均小于1,也即混合檢測的策略能夠提高檢測效率.同時每個個體的核酸檢測次數(shù)X的取值只可能有兩種:因此可以說隨機變量X服從二項分布:

如果混合樣本檢測結果為陰性,k人平均測試即:

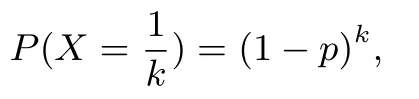
如果混合樣本檢測結果為陽性,k人平均測試次,即:

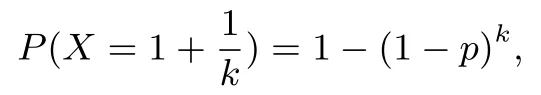
可得X的數(shù)學期望:

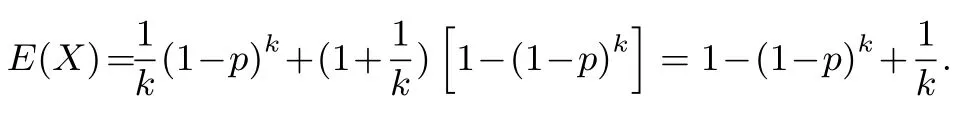
根據(jù)實際情況可知p非常小,同時根據(jù)二項式定理有:

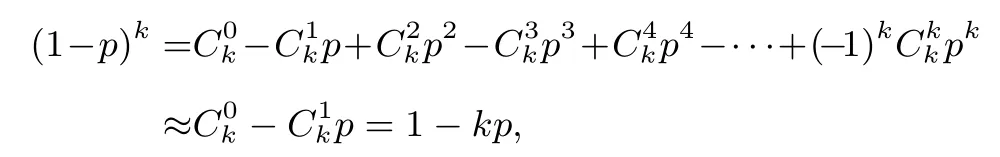
所以有:

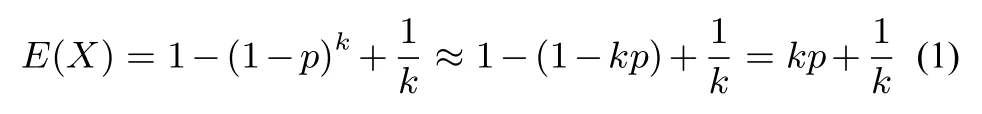
依據(jù)武漢衛(wèi)健委公布數(shù)據(jù): 武漢約1000 萬人口, 約8萬人感染新冠病毒, 感染率p約為0.008, 四舍五入可以取p=0.01 代入式(1)為:

隨著社會的發(fā)展，技術的進步，可能現(xiàn)在孩子學的許多東西到二三十年后就沒有用了，但是讓孩子做最好的自己，可以讓他們受益一輩子。

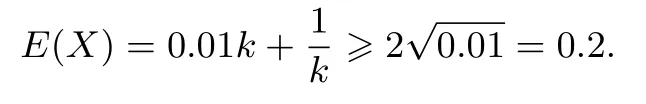
顯然E(X) 越小越好, 根據(jù)均值不等式可得當且僅當時,即k= 10 時,E(X)取最小值0.2.也就是說平均單人只需要檢測0.2 次,這約節(jié)省了80%的成本.實際上,武漢市的部分區(qū)域正是一次性將10 人的樣本混合在一起作為一組進行檢測,從而提高檢測效率.

武漢市十天大會戰(zhàn)需要核酸檢測的人數(shù)約為1000 萬,如果每天可以檢測10 萬人次的話,單次檢測則需要100 天(3 個多月).但是如果采取混合檢測的策略,就可以通過數(shù)學方法解決了這個棘手的問題.假設如上方法武漢市每10 人一組進行混檢,只需要10 天便可以完成全武漢一千萬人的核酸檢測.

三、評價與改進

以上模型通過數(shù)據(jù)運算說明了在保證正確率的前提下,最佳的混合檢測樣本數(shù).但是以上的結果當然只是理論上的期望估計值,實際檢測過程還有很多制約和干擾因素,比如,在疫情嚴重的地方我們可以采取單一檢測的方法,在病毒感染率較高情況下可以采取混合檢測的方法,以此提高效率.

核酸檢測過程中我們還可以在此地方進行改進:

(一)適當縮小混合組,這即可以減小混合樣本過多檢不準的問題, 還可以減少一個組中可能包含兩個陽性的概率.實際上武漢是使用這種方式,將5 10 人的樣本作為一組進行混合檢測。

(二)排除實踐中陽性不會呈現(xiàn)完全均勻分布問題的對檢測的干擾.我們可以根據(jù)以往的新型肺炎感染率,同時可以先將整個待測地進行預采樣,得到此片區(qū)的整體平均感染率.針對低陽性率的地區(qū)用多人分組混合檢測,較高陽性率的地區(qū)可以采用兩三人一組為混合檢測.疫情最嚴重的地區(qū)可以采用逐一檢測,即1 人1 測.

(三)重視從技術上解決個別誤檢問題.在假設誤檢概率不是很大時,現(xiàn)在采取重復檢測方法,如果有2 個檢測結果為陽性的話,則最后判定為陽性.這樣的話一次誤檢的結果也不會影響最后的結果.

四、探究推廣與應用

實踐和理論分析表明,當大量的待檢測樣本中含陽性樣本較少時,如高考考生體檢驗血、新兵入伍復查體檢驗血,組合檢測法比逐一檢測法需要的檢測次數(shù)要少.反之如果所有樣本中陽性的比較多,那么組合檢測法很有可能不僅不會減少檢測的次數(shù),還會增加檢測的次數(shù).根據(jù)Hu-Hwang-Wang猜想: 若已知有1/3 以上的樣本是壞的,則逐一檢測法是最好的[2].