對一道預賽試題的思考與探究

福建省周寧縣第一中學(355400) 葉 樺

題目(2018年全國高中數學聯賽福建賽區預賽第12 題)已知F1,F2分別為橢圓C:=1(a ＞b ＞0)的左、右焦點, 點在橢圓C上, 且ΔF1PF2的垂心為

(1)求橢圓C的方程;

(2)設A為橢圓C左頂點,過點F2的直線l交橢圓C于D,E兩點,記直線AD,AE的斜率k1,k2,若k1+k2=求直線l的方程.

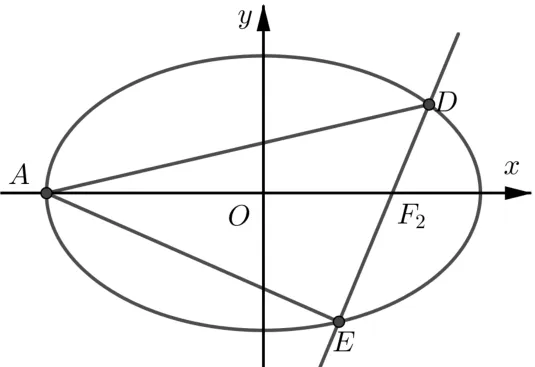
圖1

本題的答案是: (1)橢圓C的方程為直線l的方程為y= 2(x-1).本題(2)的內涵豐富,意境深邃,值得引導學生深入思考與探究.

1 由特殊到一般的思考與探究

本題的(2) 的關鍵是在“k1+k2=的條件下求出直線l的斜率k= 2.我們不禁要問: 對于一般的橢圓=1(a ＞b ＞0),若k1+k2=λ(λ為非零常數),那么,直線l的斜率k是否為某個定值?

經探究,可得

性質1.1設A為橢圓C:= 1(a ＞b ＞0)的左頂點,過焦點F(c,0)的直線l交橢圓C于D,E兩點,若直線AD,AE的斜率k1,k2滿足k1+k2=λ(λ為非零常數),則直線l的斜率k=(其中e為橢圓C的離心率).

證明設直線l的方程為x=hy+c,由λ/=0 知h/=0,直線l的斜率將直線l的方程與橢圓C方程聯立,得

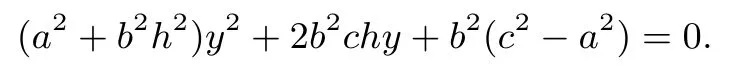
設D(x1,y1),E(x2,y2),據韋達定理,

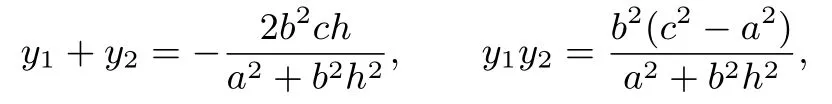
且有x1=hy1+c,x2=hy2+c.又由A(-a,0),得

性質2.1設A為雙曲線C:=1(a ＞0,b ＞0)的左頂點,過焦點F(c,0)的直線l交雙曲線C于D,E兩點,若直線AD,AE的斜率k1,k2滿足k1+k2=λ(λ為非零常數),則直線l的斜率k=(其中e為雙曲線C的離心率).

性質3.1設O為拋物線C:y2= 2px(p ＞0)的頂點,過焦點的直線l交拋物線C于D,E兩點,若直線OD,OE的斜率k1,k2滿足k1+k2=λ(λ為非零常數),則直線l的斜率k=

下面只證明性質3.1,性質2.1 可仿照性質1.1 的證明證之.

證明設直線l的方程為x=hy+由λ/=0 知h/=0,直線l的斜率k=將直線l的方程與拋物線C的方程聯立,得y2= 2p(hy+整理得y2-2phy-p2= 0.設D(x1,y1),E(x2,y2)據韋達定理,y1+y2=2ph,y1y2=-p2,且有x1=hy1+則

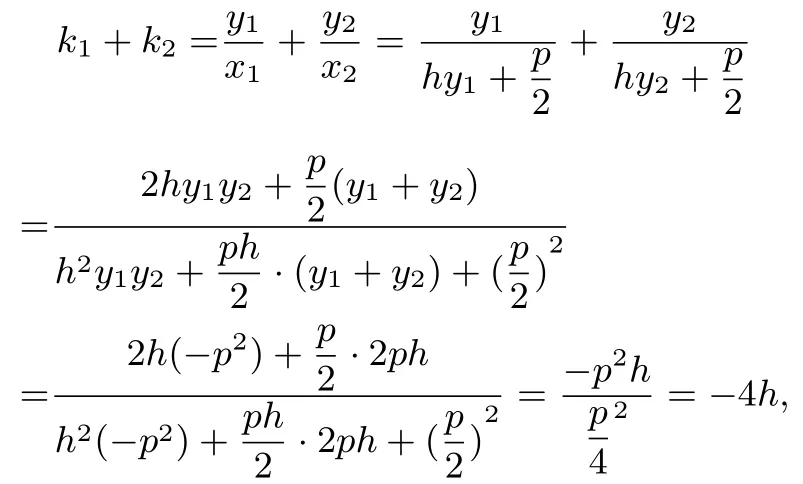
由此可得k=證畢.

2 由焦點到“類焦點”的思考與探究

以上性質揭示了圓錐曲線焦點弦所在直線的斜率,該弦兩端點與頂點連線的斜率的內在聯系,若將焦點F換為定點(m,0),那么,會有什么相應的結論? 經探究,有

性質1.2設A為橢圓=1(a ＞b ＞0)的左頂點,過定點(m,0)(0＜m ＜a)的直線l交橢圓C于D,E兩點,若直線AD,AE的斜率k1,k2滿足k1+k2=λ(λ為非零常數),則直線l的斜率k=(其中e,c分別為橢圓C的離心率,半焦距).

證明設直線l的方程為x=hy+m,由λ/=0 知h/=0,直線l的斜率k=以“m”替換性質1.1 證明中的“c”,可得

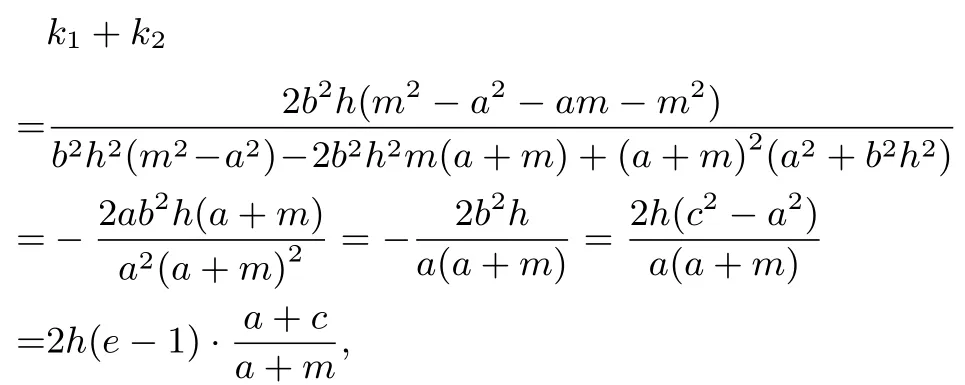
類似地,有

性質2.2設A為雙曲線C:=1(a ＞0,b ＞0)的左頂點, 過定點(m,0)(m ＞a) 的直線l交雙曲線C于D,E兩點,若直線AD,AE的斜率k1,k2滿足k1+k2=λ(λ為非零常數), 則直線l的斜率k=(其中e,c分別為雙曲線C的離心率,半焦距).

性質3.2設O為拋物線C:y2= 2px(p ＞0)的頂點,過定點(m,0)(m ＞0)的直線l交拋物線C于D,E兩點,若直線OD,OE的斜率k1,k2滿足k1+k2=λ(λ為非零常數),則直線l的斜率k=

下面只證明性質3.2,性質2.2 可仿照性質1.2 的證明證之.

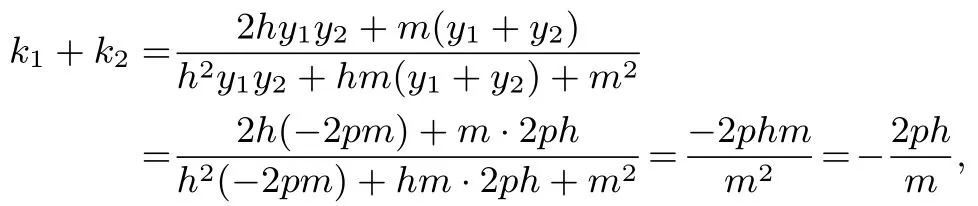
特別地,當m=c,即定點(m,0)為焦點F(c,0)時,性質1.2,2.2 分別為性質1.1,2.1;當m=即定點(m,0)為焦點時,性質3.2 即為性質3.1.

3 去掉兩個條件后的思考與探究

若去掉性質1.2, 2.2, 3.2 中的“過定點(m,0)”及“k1+k2=λ”這兩個條件, 那么直線l的斜率k與直線AD,AE(OD,OE)的斜率k1,k2是否有某種內在聯系?

經探究,有

性質1.2 的推論設A為橢圓C:= 1(a ＞b ＞0) 的左頂點, 不過點A的直線l交橢圓C于D,E兩點, 若直線AD,AE,l的斜率k1,k2,k均存在且非零, 則(其中e為橢圓C的離心率).

證明由性質1.2 的證明過程可得

2.4.1 HPLC指紋圖譜的生成 取5批樣品各適量，按“2.2.3”項下方法制備供試品溶液，再按“2.1”項下色譜條件進樣測定，采用《中藥色譜指紋圖譜相似度評價系統（2004 A版）》對5批樣品的HPLC圖譜進行分析，得HPLC指紋圖譜，詳見圖1、圖2。

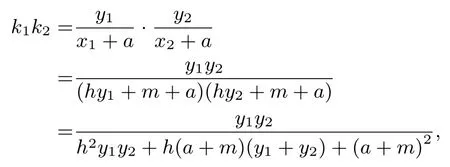
則

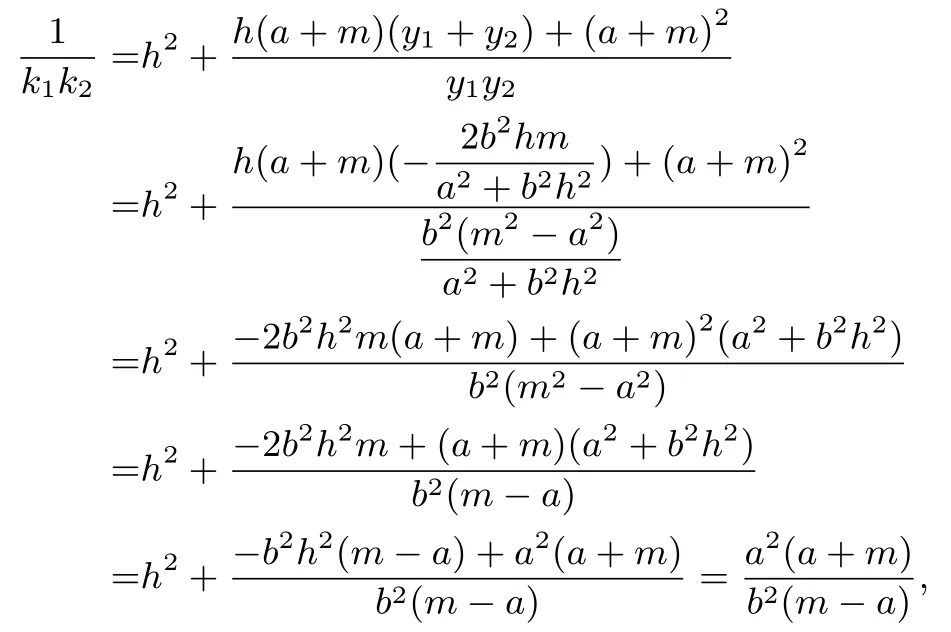
由此可解得m=代入性質1.2 的結論:得

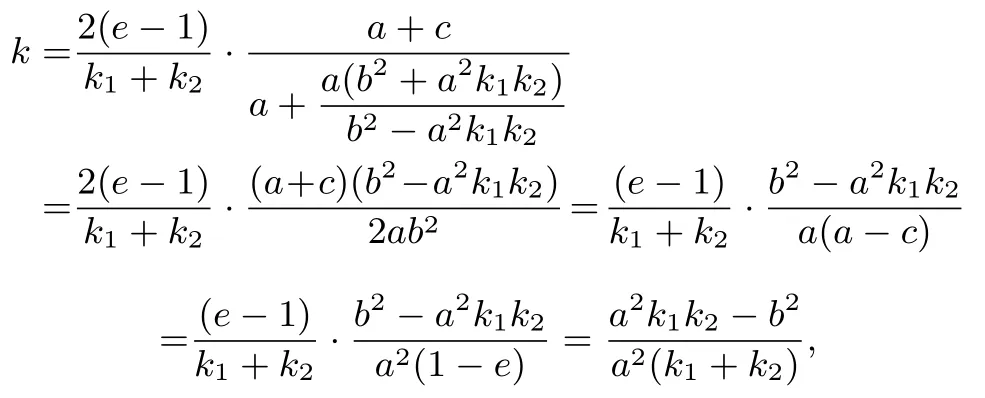
則

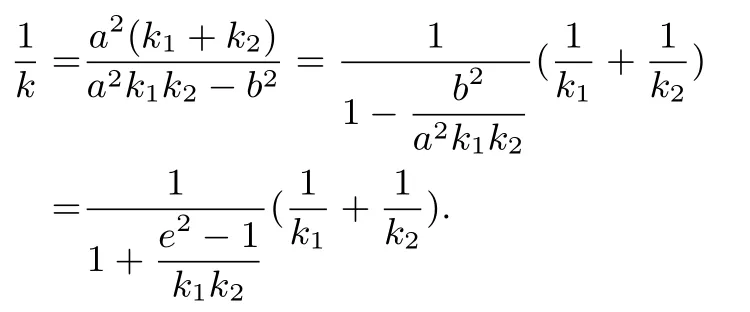
證畢.

類似地,有

性質2.2 的推論設A為雙曲線= 1(a ＞0,b ＞0)的左頂點,不過點A的直線l交雙曲線C于D,E兩點, 若直線AD,AE,l的斜率k1,k2,k均存在且非零, 則(其中e為雙曲線C的離心率).

性質3.2 的推論設O為拋物線C:y2=2px(p ＞0)的頂點,不過原點O的直線l交拋物線C于D,E兩點,若直線OD,OE,l的斜率k1,k2,k均存在且非零,則

下面只證明性質3.2 的推論,性質2.2 的推論可仿照性質1.2 的推論的證明證之.

證明由性質3.2 的證明過程可得

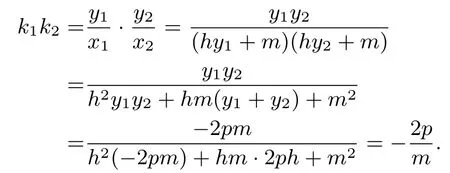
則m=代入性質3.2 的結論:k=可得證畢.

由上述三個推論,可得圓錐曲線的一個統一性質:

統一性質設A為標準圓錐曲線C的左頂點(拋物線的頂點), 不過點A的直線l交圓錐曲線C于D,E兩點, 若直線l,AD,AE的斜率k,k1,k2均存在且非零, 則(其中e為圓錐曲線c的離心率).

至此,我們完成了對上述預賽試題的思考與探究.至于橢圓,雙曲線右頂點的情形,這里不再贅述.

4 性質的應用舉例

例1(2020年南昌市一模理科第20 題) 已知圓F1:(x+1)2+y2=r2(1 ≤r≤3).圓F2:(x-1)2+y2=(4-r)2.

(1)證明圓F1與圓F2有公共點,并求公共點的軌跡E的方程;

(2)已知點Q(m,0)(m ＜0), 過點F2斜率為k(k /= 0)的直線與軌跡E相交于M,N兩點,記直線QM,QN的斜率分別為k1,k2,是否存在實數m使得k(k1+k2)為定值?若存在,求出m的值;若不存在,說明理由.

簡析(1)軌跡E的方程為= 1(過程略); (2)由a2= 4,b2= 3, 得e=據性質1.1, 得k(k1+k2) =kλ= 2(e-1) =-1) =-1,即存在橢圓E的左頂點Q(-2,0)(m=-2),使得k(k1+k2)為定值-1.

例2(2012年第3 屆世界數學團體錦標賽青年組個人賽第4 輪第13 題)經過拋物線y2= 2px(p ＞0)的頂點O作兩條弦OA和OB,若OA、OB的斜率k1,k2恰好為方程x2+4x-2=0 的兩個根,求直線AB的斜率k.

簡析由條件得k1+k2=-4,k1k2=-2,據性質3.2的推論,