探究直觀想象在非幾何問題中的運用

廣州市南沙麒麟中學(511455) 武志容

新的課程標準指出高中數學教學由以前的三維目標: 知識與技能、過程與方法、情感態度與價值觀上升到六大核心素養: 數學計算、數學抽象、直觀想象、邏輯推理、數據分析、數學建模,從學生個人的技能提升到個體的全面發展,從具體的操作步驟到高度的概括提煉,是從量變到質變的一個飛躍,也從更高程度上要求我們在整個高中數學的學習過程中要高度的重視和不斷的滲透這些核心素養,只有掌握好了它們才能真正的學好高中數學,才能在各種考試中立于不敗之地.新教材新高考倡導的新題型很多時候也需要我們有很好的直觀想象能力作為一個突破點.

直觀想象可以說是這六大核心素養中最容易理解和接受的,但正如武術中的太極一樣,看似簡單卻不易掌握,只有真正的武林高手才能做到游刃有余、以柔克剛、化腐朽為神奇.眾所周知幾何問題是直觀想象的最好體現,除此之外直觀想象在非幾何問題中也有非常多的運用,我們結合近幾年的高考題重點考察非幾何問題.

一、有圖有形,直觀+想象

例1(2020年高考全國Ⅰ卷理科第5 題)某校一個課外學習小組為研究某作物種子的發芽率y和溫度x(單位°C)的關系,在20 個不同的溫度條件下進行種子發芽實驗,由實驗數據得到下面的散點圖:

由此散點圖,在10°C至40°C之間,下面四個回歸方程類型中最適宜作為發芽率y和溫度x的回歸方程類型的是( )

A.=ax+bB.y=a+bx2C.y=a+bexD.y=a+blnx

解題分析這道圖形題非常的直觀,但不同層次的同學看到這道題的感覺是不一樣的: 低層次的同學會馬上錯選A,因為就回歸方程來講線性回歸方程相對比較熟悉,平時練習也較多;中層的同學可能關注點是在這20 個數據上,雖然給了坐標但沒有給出具體的對應值,只能估算,但20 個數據估算起來也很困難,況且這里的a,b都未知,所以最后會陷于一種比較困惑的狀態;稍好的同學會知道直接看圖再加一點自己的想象,不需要計算,只需根據圖形的大致形態,再結合各個函數圖象的特點,直接找出與之吻合度較好的對數函數模型,直接看出答案D,既快又準.

像這種有實際應用背景的題目是近幾年高考的熱點題型,它把數學融入實際生活中,讓我們了解數學在生活中的應用情況,并深刻體會到數學是一門非常有用的學科,它不同于一些純數學問題的常規題,往往會配給一些圖形,給人比較新穎、有趣的感覺,但題目本身又不會很難,計算、技巧、方法其實要求都不高,以估算、想象、聯想為主,它更側重的是思維的靈活,大局意識、整體把握,不拘泥于局部的某一個細節,有一定的創新性,更符合當下我們培養人才的目標和方向.

與之類似的還有去年的網紅高考題(維納斯的身高問題).

例2 (2019年高考全國Ⅰ卷理科第4 題)古希臘時期, 人們認為最美人體的頭頂至肚臍的長度與肚臍至足底的長度之比是≈0.618, 稱為黃金分割比例),著名的“斷臂維納斯”便是如此．此外,最美人體的頭頂至咽喉的長度與咽喉至肚臍的長度之比也是．若某人滿足上述兩個黃金分割比例,且腿長為105 cm,頭頂至脖子下端的長度為26 cm,則其身高可能是( )

A.165 cm B.175 cm C.185 cm D.190cm

解題分析同樣這道題從直觀上來看是可以估算的.從一個黃金比例出發, 如頭頂至咽喉的長度與咽喉至肚臍的長度之比為求出咽喉至肚臍的長度大致為≈0.618?x ≈42,總身高約為26+42+105=173cm,比較接近的就是答案C.計算并不復雜,可以非常快速精準的找到答案.但很多同學卻陷于精確計算里面了,咽喉與脖子下端有一個長度,肚臍到腿也有一個長度又該怎么算呢?其實此題的目的就是考察學生的直觀想象+估算,最后的問題也是“其身高可能是”,說明不需要精確計算.另外從整個人體來看那些小長度可以忽略不計或者憑我們的直觀給它一個估值,而從選項來看各個長度差距也比較大,10cm 的誤差范圍說明也不要糾結于那些不可知的小長度,所以說直觀想象+估算用的好,完全可以起到事半功倍的效果.

二、無圖有形,想象+逆向

例3(2020年高考全國Ⅰ卷理科第22 題)在直角坐標系xOy中,曲線C1的參數方程為(t為參數).以坐標原點為極點,x軸正半軸為極軸建立極坐標系,曲線C2的極坐標方程為4ρcosθ-16ρsinθ+3=0.

(1) 當k=1 時,C1是什么曲線?

(2) 當k等于4 時,求C1與C2的公共點的直角坐標.

解題分析(1)略.(2)主要是參數方程

的化簡比較困難.可以說這是一道沒有圖的題目,但有比較工整的“形”—參數方程關于方冪通常我們做的比較多的變形是低次往高次上化,如

特別是sin4t=(sin2t)2,cos4t=(cos2t)2.

這是很多同學都能想到的,但反過來

很多同學可能就想不到,所以這道題做不下去基本上就是卡在這個點上.當出現問題的時候不妨多觀察一下這個式子的特點,我們說美的式子也是一種圖形,并非有圖才直觀,無圖想象也要直觀.數形結合、定性分析已經成為高考試題的重要組成部分.反復觀察下面的式子:

想象一下它們之間的關系

不難想到

所以

這兩個幾乎同樣的式子顯示出的規律其實非常明顯,多看幾遍不難發現它們之間主要存在平方關系,平方逆運算就是開方.題目的用意就是要我們將四次方式反過來化為二次方式,這里就充分體現了我們老師在講新課的時候有沒有著重滲透平方與開方互為逆運算這樣的一種數學思想方法.

逆向思維是我們想象的一個方向,也通常是我們創新能力培養的一個重要途徑,如加法與減法、乘法與除法、乘方與開方、導數與積分、三角函數與反三角函數、函數與反函數等等,逆向思維用的好就可以很好的舉一反三、觸類旁通,更好的加深對概念的認識和理解,更好的把握數量關系和圖形特點的本質.該題目的是通過對式子所呈現出來的“形”進行直觀想象來觸發學生的逆向思維進而實現創新能力的提升,這種變形變式能力也是數學常用的方法技巧之一,此題與2019年高考全國Ⅰ卷理科第22 題有異曲同工之處:

例4(2019年高考全國Ⅰ卷理科第22 題)在直角坐標系xOy中,曲線C的參數方程為(t為參數)．以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,直線?的極坐標方程為2ρcosθ+

(1)求C和?的直角坐標方程;

(2) 求C上的點到?距離的最小值.

解題分析這道題的式子也是一個非常好的“形”,由這個式子可以聯想到很多數學公式,如: 平方差公式、完全平方公式、三角函數公式等,所以這道題也有很多巧妙的解法,如:

或作三角代換t=用三角萬能公式:

再代入三角函數的公式sin2α+cos2α=1 等.

但如此精巧的解法很多中下層同學很難看出來或根本想不到, 更別說是在緊張的高考考場上了.此時一定不能盲目的去做, 而是要停下來多觀察式子的特點, 直觀感覺找準切入點—想辦法先換算出t, 但兩個式子好像都不太好求出t, 其實仔細觀察后不難發現上式比較容易先化出然后將t2整體代入下式就可以換出t,再利用t與t2的關系消去參數t,從而得到x,y的直角坐標方程.

這里學生只要明白一個核心觀念就可以了: 知道了t2也就等價于知道了t,再把它當做已知量繼續代入其他式子就一定能換出t.有了這個“定海神針”作為支撐,哪怕中間步驟繁瑣一點,還是有足夠的信念堅持能做出來的,相比較想不出巧妙解法而不知從何下手,我覺得這種做法更直觀更切實有效.所以說很多時候我們看待數學問題要有整體意識、逆向思維,要更側重數學思想方法的把握,打開我們僵化的思維、開闊我們的視野,思維的導向往往比方法、技巧更重要.

三、無圖無形,直觀+猜想

例5(2020年高考全國Ⅰ卷第21 題)已知函數f(x) =ex+ax2-x,

(1)當a=1 時,討論f(x)的單調性;

(2)當a=1 時,f(x)≥求a的取值范圍.

解題分析這道題既沒有圖也沒有形式工整的式子—“形”,但該題大部分同學都知道基本方法是利用導數工具來解決函數的性質問題,沿著這個思路一步步往下做看能發現什么.在做第一小問時

直接觀察可以得出該導函數是增函數(因為y= ex和y=2x-1 都是增函數),但找出方程的根有點困難.令

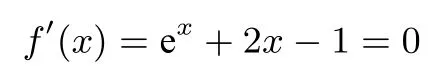
這是一個超越方程, 在中學范圍內沒有確定的方法求解, 要找出它的根, 就只能靠我們的經驗或直觀+猜想了,如果把x=0直接代入會發現方程是成立的,所以馬上發現0 就是它的一個根, 再結合單調遞增的性質可以大致想象出其導函數f′(x)=ex+2x-1,的圖象如上圖所示.

根據導數的圖像特征,原來的函數f(x) = ex+x2-x的單調性就很清楚了: 當x ＞0 時,f′(x)＞0,f(x)單調遞增;當x ＜0 時,f′(x)＜0,f(x)單調遞減.

做第二問時同樣也需要直觀+ 猜想來助攻.首先將式子分類, 構建出新的函數: 當x= 0 時, 待證不等式恒成立,a ∈R; 當x ＞0 時,a ≥恒成立, 令h(x) =, 所 以h′(x) = 令h′(x) = 0, 其 中g(x) =- x -1 = 0 的根也需要憑我們的直觀觀察出來,嘗試把x=0 代入進去發現仍然是成立的！(屢試不爽)說明x= 0 是它的一個根,還有沒有其他的根? 這個時候就需要用單調性來保證根的唯一性,所以想到需要再進行求導來判斷.

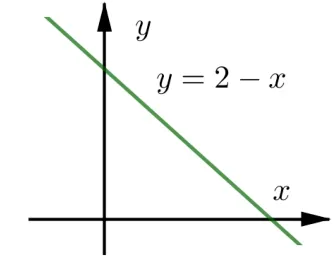
令g′(x) = ex - x -1, 直觀發現g′(0) = 0;再次求導g′′(x) =ex -1,當x ＞0 時,g′′(x)＞0,說明g′(x) 單調遞增, 所以當x ＞0時,g′(x)＞g′(0) = 0, 說明g(x)也是單調遞增, 因此g(x)＞g(0) = 0, 因此對于h′(x) =只要考察s(x) = 2-x這部分的正負情況就可以了, 再次借助于它的圖象可知: 在(0,2)內,h(x)單調遞增; 在(2,+∞)內,h(x)單調遞減, 所以h(x)max=h(2)=從而a ≥

整道題的關鍵點其實還是幾個超越方程的求根問題,好像超過我們中學數學的范疇,但實際上憑我們的解題經驗和對數學的直觀想象一般都能直接看出方程的根,如果不具備這樣的核心素養,一味的鉆進去求解計算往往最后就做不下去.類似的問題還有下面的這些導數題:

題目1(2019年高考全國Ⅰ卷理科第20 題)已知函數,f(x)=sinx-ln(1+x),f′(x)為f(x)的導數．證明:

(1)f′(x)在區間存在唯一極大值點;

(2)f(x)有且僅有2 個零點．

題目2(2018年高考全國Ⅰ卷理科第21 題) 已知函數

(1)討論f(x)的單調性;

(2)若f(x)存在兩個極值點x1,x2,證明:＜a-2.

再如下面的向量題:

例6(2020年全國Ⅰ卷理科第14 題)設a,b為單位向量,且|a+b|=1,則|a-b|=____.

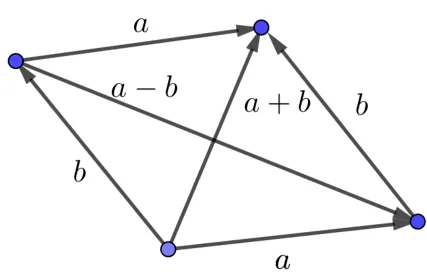
解題分析該題看上去跟圖形沒有任何關系, 但可以根據數的特點直觀想象出圖形來.根據|a|=|b|=1,|a+b|= 1 可以想象出一個等邊三角形, 再利用向量三角形運算規則馬上可以得出|a-b|就是鈍角三角形中120°所對的邊長能想象出圖形出來這道題計算起來也就非常簡單.

縱觀近幾年的高考題不難發現直觀想象這一數學核心素養的提升是一個趨勢, 無論是數還是形都要求越來越高.有圖直觀好想象,無圖想象也要直觀,再利用數形結合、定性分析、全局意識、整體把握、逆向思維、···,往往能達到攻無不克,無堅不摧的效果！事實上我們現在的科研需要有方法有技巧,更需要創新,直觀感受往往是創新的起點,再加上豐富的想象和大膽的猜想,最后用我們的邏輯推理、數據分析、數學計算等方法技巧來加以核實和驗證從而成就我們的偉大創新和發現.所以說沒有很好的直觀想象就很難有創新和發現,也就不會有我們今天的科技進步！