從射影幾何視角分析北京高考解析幾何試題

北京市第五中學通州校區(101101) 田朋朋 何 偉

近年來,各地高考試題中以射影幾何中極點極線、中心射影理論為背景的圓錐曲線題目層出不窮.本人在文[1]中分析了2019年北京高考數學文科解析幾何試題命制的背景為射影幾何中極點極線理論下的反演變換.本人在文[2]中借助射影幾何中的極點極線、中心射影理論揭示了一類圓錐曲線中三直線斜率等差性質的本質,并推廣出十個優美結論.分析試題背后的命題思路,有助于學生對試題結果進行猜想和假設,從而更好的書寫過程和運算結果.同樣對于教師,如果了解試題命制背后的思維邏輯,可以通過對高考試題進行橫向、縱向研究,命制與高考相似的變式訓練,對學生進行有針對性的思維訓練,提高學生的邏輯思維能力.

1 射影幾何相關理論

1.1 點列交比

若A,B,C,D四點共線, 則這四點A,B,C,D的交比(AB,CD) 定義為四條有向線段的比: (AB,CD) =若(AB,CD) =-1,則稱點C,D調和分割點A,B,或稱點A,B與點C,D調和共軛,A,B,C,D為調和點列.如圖1.

特別地有: (1)最左(右)側點到同側三點的線段成調和關系:

(2)一線段被它的中點和這直線上的無窮遠點調和分割.

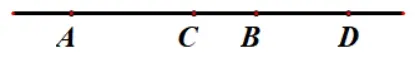
圖1

圖2

1.2 線束交比

若a,b,c,d是共點的四條直線, 則(ab,cd) =叫做a,b,c,d的交比.若四直線a,b,c,d滿足(ab,cd)=-1,則稱a,b,c,d調和共軛.如圖2.

特別地有: (1)如果任意一條直線s截a,b,c,d四條直線于點A,B,C,D,則有(ab,cd)=(AB,CD).

(2) 若公共點記為P, 習慣上將(ab,cd) 記為P(AB,CD).

(3)若共點四直線a,b,c,d的斜率分別為k1,k2,k3,k4,則(ab,cd)=

(4)交比經中心射影后不變.

1.3 極點極線理論

如圖3, 給定二次曲線C, 如果兩點P,Q(P,Q不在曲線C上) 的連線與二次曲線交于兩點M1,M2, 且(M1M2,PQ) =-1, 則稱P,Q關于二次曲線C調和共軛,或稱點Q與點P關于二次曲線C互為共軛點.

不在二次曲線上的一個定點關于一條二次曲線調和共軛點的軌跡是一條直線.若定點P關于二次曲線的共軛點的軌跡是一條直線,這條直線叫做點P關于此二階曲線的極線,P點叫做這條直線關于此二次曲線的極點.若點P在二次曲線上,則點P的極線即為二次曲線在P點處的切線.

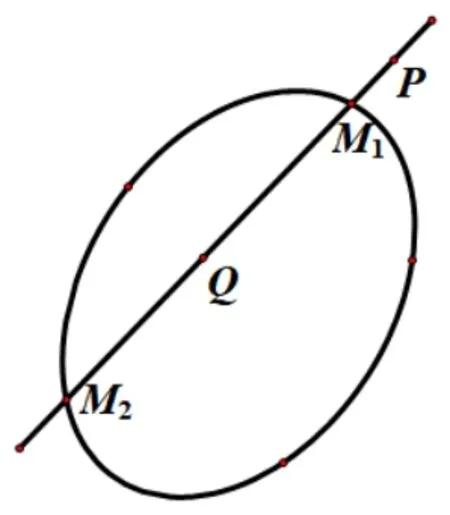
圖3

圖4

如圖4,P為不在二次曲線上的點,過點P引兩條割線依次交二次曲線于點E,F,G,H, 連接EH,FG交于點N,連接EG,FH交于點M,則MN為點P對應的極線.特別地,若P是二次曲線上的點,則過點P的切線即為極線.同理直線PN為點M對應的極線,直線PM為點N對應的極線.

在《高等幾何》[3]中, 點P(x0,y0) 關于二次曲線C:Ax2+Bxy+Cy2+Dx+Ey+F=0 的極線方程為

即(2Ax0+By0+D)x+(Bx0+2Cy0+E)y+Dx0+Ey0+2F=0.特別地有:

(3)對于拋物線y2=2px,與點P(x0,y0)對應的極線方程為y0y=p(x0+x);

(4)圓錐曲線的焦點與準線是一對特殊的極點與極線.

限于文章篇幅,上述1.1 中的(1)和(2);1.2 中的(3)和(4);1.3 中的(1-4)在此不做證明,證明過程請參見文[4].

2 命題背景分析

試題1(2020年高考北京卷第20 題) 已知橢圓過點A(-2,-1),且a=2b,

(1)求橢圓C的方程;

(2)過點B(-4,0)的直線l交橢圓C于點M,N, 直線MN,MA分別交直線x=-4 于點P,Q,求的值.

分析如圖5, 因為橢圓方程為= 1, 所以a2= 8, 點B(-4,0) 的極線為x==-2, 可知定點A(-2,-1) 在點B(-4,0) 的極線x=-2 上, 設極線x=-2 與線段MN交于點D,由極點極線的定義可知A(BD,MN) =-1,又因為交比在中心射影下不變,所以有A(BD,MN) =A(BB∞,PQ) =-1(B∞為點B的無窮遠點).即線段PQ被點B和點B的無窮遠點調和分割,所以點B為線段PQ的中點,因此

圖5

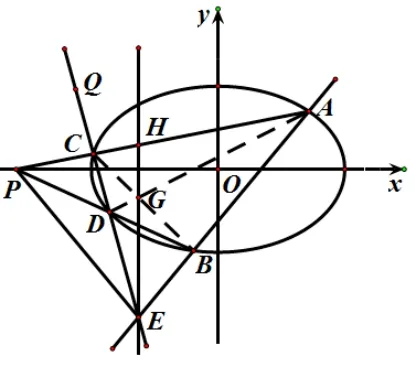
圖6

試題2(2018年北京卷文科第20 題) 已知橢圓M:= 1(a ＞b ＞0) 的離心率為焦距為斜率為k的直線l與橢圓M有兩個不同的交點A,B,

(1)求橢圓M的方程;

(2)若k=1,求|AB|的最大值;

(3) 設P(-2,0), 直線PA與橢圓M的另一個交點為C, 直線PB與橢圓M的另一個交點為D, 若C,D和點共線,求k.

分析本題與試題1 有著相同的幾何背景,都是以橢圓為基礎的中心射影結構.如圖5,將本試題中橢圓上的四個點A,B,C,D退化為三個點(點B,D,E重合)后,就是圖5 的幾何結構.只不過試題2 是在解決以點E為中心射影的四條直線斜率關系問題,試題1 是在解決同一中心射影下交比不變的問題.

又因為直線EH垂直于x軸, 所以可認為kEH=∞, 則有= 1, 即kEP - kEC=kEB - kEP, 即2yE -4(yE -=k-2yE,解得k=1.

試題3(2018年高考北京卷理科第19 題)已知拋物線C:y2= 2px經過點P(1,2),過點Q(0,1)的直線l與拋物線C有兩個不同的交點A,B,且直線PA交y軸于點M,直線PB交y軸于點N.

(1)求直線l的斜率的取值范圍;

(2)設O為原點,為定值.

分析從射影幾何的眼光下看,橢圓、雙曲線、拋物線可看作圓在某一平面上的投影,三種曲線的各自定義、統一定義及其幾何性質有著密切的聯系.本試題與試題1 有著相同的幾何背景,只不過將試題1 中的橢圓換成拋物線、x軸上的定點B(-4,0)換成y軸上的定點Q(0,1).

圖7

具體分析過程如下: 如圖7,連接OP交AB于點C,則直線OP方程為y= 2x.因為拋物線的方程為y2= 4x,所以點Q(0,1) 的極線為y= 2x, 即為直線OP.所以有P(AB,CQ) =-1,又因為交比在中心射影下不變,所以有P(MN,OQ) =P(AB,CD) =-1,即點M,N調和分割點Q,O.因此有

試題4(2017年高考北京卷理科第18 題)已知拋物線C:y2=2px過點P(1,1).過點作直線l與拋物線C交于不同的兩點M,N, 過點M作x軸的垂線分別與直線OP,ON交于點A,B,其中O為原點.

(1)求拋物線C的方程,并求其焦點坐標和準線方程;

(2)求證:A為線段BM的中點.

分析本題與試題3 的幾何背景完全一致, 只不過本題中第二條截線為過點M且垂直于x軸的垂線; 試題3 中第二條截線為y軸.根據交比在中心射影下的不變性,本題第(2)問的結論又與試題1 完全一致.

圖8

具體分析如下: 如圖8, 連接OP交MN于點C, 則直線OP方程為y=x.因為拋物線的方程為y2=x,所以點的極線為y=x, 即為直線OP.所以有P(DC,MN) =-1.并且當點D,C,M,N為一組調和點列時, 以點P為中心的線束中直線的交比等于以點O為中心的線束之中直線的交比, 即P(DC,MN) =O(DC,MN) =-1.又因為交比在中心射影下不變,所以有O(DC,MN) =O(A∞A,MB) =-1(A∞為點A的無窮遠點),即線段MB被點A和點A的無窮遠點調和分割,所以點A為線段BM的中點.

3 結語

由此可見,近幾年高考北京卷解析幾何試題的幾何背景完全一致,都是在射影幾何背景下,由一些特殊的點、線關系造成的定點、定值問題.本人認為此類試題備受青睞的原因有:

一、圓錐曲線可以看作平面內點的運動軌跡,在體現著運動變化思想的同時,也蘊藏著運動變化過程中保持的某種“不變性”.

二、定點、定值類問題不但結論美觀,覆蓋知識面廣,而且符合數學抽象與直觀想象能力、邏輯推理與數學運算能力的考察要求.

三、圓錐曲線中的橢圓、雙曲線、拋物線可看作圓在某一平面上的投影,三種曲線之間存在著相同的幾何性質,為命題者設計圓錐曲線問題中的“不變”提供了思路與方向.

作為一名高中教師, 了解一些與射影幾何相關的理論,可以登高望遠,以較高的觀點去認識與看清高考解析幾何試題,有利于中學數學的教學.克萊因也認為: 基礎數學的教師應該站在更高的視角來審視、理解初等數學問題,只有觀點高了,事物才能顯得明了簡單[5].