基于特征挖掘的indRNN光伏發電功率預測

王超洋，張藍宇，劉 錚，譚 娟，徐 晟

（1.國網湖南省電力有限公司長沙供電分公司，長沙 410200；2.長沙理工大學電氣與信息工程學院，長沙 410114）

2018年我國新增光伏裝機量達到44.1 GW，截止2018年底我國光伏裝機總量達到174.0 GW，新增和累計裝機量均為全球第一[1]。由于光伏出力受天氣影響，具有較大隨機性，會對電力調度產生一定影響[2]。準確的光伏出力預測可以應對如因光伏出力變化導致配網網損增加[3]等問題。

目前學者對提高光伏出力預測精度的方法已進行較多研究，主要有物理法和統計學習法兩種方式。物理法是基于地基云圖建立的超短期預測模型，雖然效果精度較高[4-5]，但是用于采集地基云的設備昂貴，不利于工程的實際使用。統計學習法是根據光伏出力相關數據建立機器學習模型或統計模型進行預測的方法。文獻[6-7]分別提出在反向獨播BP（back propagation）神經網絡基礎上改進的小樣本學習方法，此類方法能夠在光伏樣本少的情況下進行預測，但僅僅是針對樣本不夠時的一種備選方法。文獻[8-10]考慮了相似日或者相似時段的光伏出力模式，根據不同天氣類型對光伏出力預測建立了BP神經網絡、Elman神經網絡和Spiking神經網絡模型，對于單一天氣類型的日光伏出力預測取得了較好的效果，但是對于一天經歷多種天氣類型的日光伏出力預測效果較差。文獻[11]采用多種灰色預測模型進行組合的方法對光伏出力預測進行建模，但由于模型未參考天氣等信息，導致預測精度有限。文獻[12-14]均采用深度學習模型對光伏出力進行預測，但未進一步挖掘影響光伏出力的因素。

綜上，本文首先對光伏出力的影響因素進行深度挖掘并構造相應特征，并根據已知特征挖掘構造出其他可用特征，然后采用深度學習模型獨立循環神經網絡indRNN（independently recurrent neural network）對光伏發電功率進行預測。

1 光伏出力特征挖掘與構造

光伏出力與輻照度及轉換率有很強的關系，影響光伏出力的根本因素只有兩個，包括太陽能電池實際接受的輻照度和電池板面溫度，天氣、濕度、氣溫等都是通過影響上述兩個根本因素，進而對光伏出力產生影響的。文獻[15]證明了光伏發電與氣象因素（即輻照度、氣溫、相對濕度、風速、清晰度）有較強相關關系。

1.1 光伏實際功率與相關因素分析

根據光伏發電原理，太陽輻照度與光伏實際發電功率呈現正相關關系，光伏實際發電功率很大程度由輻照度決定，光伏實際功率與輻照度的關系如圖1所示。因為溫度與輻照度呈正相關關系，溫度與光伏實際功率也有一定相關性，如圖2所示。由圖3～圖6可見，濕度、風速、風向和壓強與光伏實際功率并沒有明顯的線性關系（為減小因數值差異過大而影響模型學習，圖2、圖3、圖4和圖6中的溫度、濕度、風速和壓強值已歸一化處理），因此需要人工去構造一些特征，然后利用深度學習算法去主動挑選和學習此類特征與光伏實際功率的內在聯系，以便模型能夠更好地反映其與光伏實際功率之間的關系。

圖1 光伏實際功率與輻照度的關系Fig.1 Relationship between actual photovoltaic power and irradiance

圖2 光伏實際功率與溫度的關系Fig.2 Relationship between actual photovoltaic power and temperature

圖3 光伏實際功率與濕度的關系Fig.3 Relationship between actual photovoltaic power and humidity

圖4 光伏實際功率與風速的關系Fig.4 Relationship between actual photovoltaic power and wind speed

圖5 光伏實際功率與風向的關系Fig.5 Relationship between actual photovoltaic power and wind direction

圖6 光伏實際功率與壓強的關系Fig.6 Relationship between actual photovoltaic power and pressure

1.2 光伏實際功率預測特征構造

當預測光伏實際功率時，需要先得到輻照度。為提高光伏發電功率預測精度，本文根據原始特征數據，即時間、輻照度、溫度、濕度、風速、壓強、風向構造出如下幾類特征。

（1）輻照度有較強的周期性，因此構造兩種特征來表征，即峰值距離和最大輻照度，前者代表與每個周期峰值的距離，后者代表輻照度峰值的實際值。圖7為峰值距離輻照度特征構造方法。

圖7 峰值距離輻照度特征構造方法Fig.7 Construction method for dis2peak irradiance feature

（2）時間特征表示不同時間下光伏發電功率和氣象特征呈現不同的變化趨勢。

（3）提取白天范圍內的輻照度、溫度、濕度、風速、壓強風向等特征的均值和標準差。

（4）將第3類特征進行組合，包括特征A±特征B、特征A×特征B、特征A/特征B。

（5）各因素差值構造，例如白天溫差為白天時最大溫度和最小溫度差值，其他因素差值做相同處理。

2 光伏實際功率預測方法

2.1 基于indRNN的光伏預測模型

由于傳統循環神經網絡RNN（recurrent neural network）均采用tanh和simoid作為激活函數，會導致RNN在反向傳播時產生梯度消失的情況。因此，一些學者研究出了RNN的變體，即長短期記憶神經網絡LSTM（long short-term memory）和門控循環單元GRU（gated recurrent unit）兩種循環神經網絡，中間傳遞添加了門控制結構可以解決循環層自身傳遞的梯度消失，但對于多循環層堆疊的情況還是無法避免梯度消失。文獻[16]提出一種indRNN模型，該模型能避免傳統RNN神經元的梯度爆炸，也能解決多層LSTM和多層GRU傳遞中的梯度消失。

RNN的時間維度展開圖如圖8所示，其傳遞公式可表示為

圖8 RNN時間展開圖Fig.8 RNN time expansion map

式中：xt、ht分別為t時刻輸入和隱層的傳遞狀態，xt∈RM，ht∈RN；W、U和b分別為當前輸入、循環結構上層輸入和偏置項的權重，W∈RN×M，U∈RN×N，b∈RN；V為輸出層的權重，V∈RM×N；c為輸出層的偏置，c∈RM；o為RNN的輸出，o∈RM。

若RNN的目標函數為L，則L在T時刻的反向傳播過程可表示為

式中，diag（·）為取對角矩陣運算，式（3）為雅可比矩陣。由于矩陣對角元素進行連乘，當元素大于1時結果會變為無窮大，這種現象稱為梯度爆炸；當元素小于1時，連乘會造成結果等于0，這種現象稱為梯度消失。因此，RNN容易出現梯度消失，導致梯度下降算法不能更新到極小值。

indRNN將式（1）中的矩陣乘法修改為點乘，權重矩陣U變為向量u。此時，當前神經元只接收當前輸入和t-1時刻的自身狀態值，即

式中，⊙表示矩陣點積。通過式（2）得到indRNN的輸出o。

n層indRNN堆疊情況下的傳遞公式為

indRNN結構在反向傳播求導時能消除矩陣的連積操作，并去掉激活函數的導數與循環權重系數，從而可以使用Relu做為其激活函數進而不會出現梯度問題。

圖9 indRNN時間展開圖Fig.9 indRNN time expansion map

選定indRNN的損失函數均方誤差MSE（mean squared error）為

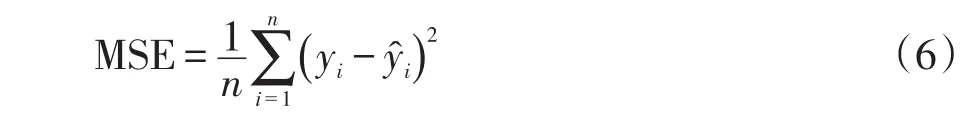
式中：yi為實際光伏功率；為預測光伏功率。

indRNN的光伏功率預測流程見圖10，將經過構造特征構造處理后的特征值輸入indRNN模型，得到光伏功率的預測值。

圖10 模型預測流程Fig.10 Model prediction process

2.2 光伏實際功率預測評價方法

光伏功率預測的評價指標選定如下。

（1）R2（R-squared）表示為

（2）均方根誤差MAE（mean absolute error）表示為

（3）平均絕對百分誤差MAPE（mean absolute percentage error）表示為

3 算例仿真

選取某個光伏電站的實際數據共計41 853條，數據采樣周期為15 min，時間范圍從2017年1月1日00：00：00至2018年4月26日 04：00：00，將全部數據中前33 853條作為訓練樣本，后8 000條作為測試樣本。

樣本中包含時間、輻照度、風速、風向、溫度、壓強、濕度。根據第2節進行特征構造，采用如下公式對數據進行標準化：

式中：μ為該特征的均值；σ為該列特征的方差。

選用5個模型對原始特征和經特征構造后的特征分別建模訓練和預測。模型及其參數見表1，其中，indRNN、LSTM、BP神經網絡的參數為每層的單元數、支持向量回歸SVR（support vector regression）的參數為懲罰系數C和gamma參數γ，K最近鄰KNN（K-nearest keighbor）算法的參數為k值。

表1 5個模型參數Tab.1 Parameters of five models

采用以上5個模型分別對使用原始特征和特征構造后的特征進行建模，預測結果包含各類型復雜天氣情況，從而展示不同天氣變化情況下的光伏實際功率預測。

表2給出了8 000個采樣點的預測值的MAE、R2、MAPE，可以看出，經過特征構造后的模型精度有很大程度的提高。

表2 各個模型預測結果Tab.2 Prediction results of each model

為了詳細驗證indRNN模型的有效性，對不同天氣情況下各模型的預測結果進行分析，本文只考慮06：00—18：00的光伏發電功率。

圖11展示了晴天下光伏發電功率預測結果，可以看出，各模型都能較好地擬合出實際光伏發電功率，而indRNN模型的功率預測曲線更加貼合真實值的變化規律。由表3可知，indRNN模型預測結果的MAE、R2、MAPE相對其他模型預測結果具有優勢。

圖11 晴天下光伏發電功率預測對比Fig.11 Comparison of photovoltaic power generation prediction on one sunny day

表3 晴天時模型預測結果Tab.3 Model prediction results on one sunny day

圖12展示了天氣變化情況下（設定上午為晴天，下午為陰天）光伏功率預測結果，可以看出，僅有indRNN模型預測功率與該天氣下實際功率有大致相同的變化，說明該算法能較好地預測天氣變化情況下光伏發電功率。從表4可以看出，在天氣變化情況下，所有模型的預測準確率都會大幅度下降，但是indRNN具有最高的準確率。

圖12 天氣變化下光伏發電功率預測對比Fig.12 Comparison of photovoltaic power generation prediction under weather changes

表4 天氣變化下模型預測結果Tab.4 Model prediction results under weather changes

圖13展示了陰天下光伏功率預測結果，可以看出，在這種情況下，只有indRNN和LSTM模型預測結果能大致擬合實際光伏發電功率曲線。從表5可以看出，indRNN模型比LSTM模型的預測準確率更高。

圖13 陰天時光伏發電功率預測對比Fig.13 Comparison of photovoltaic power generation prediction on one cloudy day

表5 陰天時模型預測結果Tab.5 Model prediction results on one cloudy day

通過對比3種天氣情況下各模型的光伏發電功率預測結果，可以看出，indRNN模型既具有LSTM模型的記憶能力，又具有更好的泛化能力，充分證明了該模型的優越性。

4 結語

光伏發電受到輻照度、溫度、濕度等因素的影響，其不確定性會對電網規劃、調度及穩定運行帶來不利影響，需要對光伏發電功率進行精確預測，以減少其負面影響。本文提出一種基于特征挖掘和indRNN模型的光伏發電功率預測模型。由人工構造大量相關特征，再由模型自我學習相關特征對光伏出力的影響，這樣不僅提高了預測精度，更能節省特征挑選的時間。