如何在數學概念課中,實現深度教學?


摘要:深度教學是發展學生思維能力、提升學生核心素養的一種必然之路,它可以借助于引導性材料在“教什么”中體現;可以在知識的生成過程中體現;還可以在學生的思維碰撞中體現。
關鍵詞:概念教學;知識生成;深度教學
中圖分類號:G633.6 文獻標識碼:A文章編號:1992-7711(2021)01-017
深度教學是發展學生思維能力、提升學生核心素養的一種必然之路,那么如何在數學概念課中實現深度教學呢?本文試結合《數列概念》的教學談一談筆者的想法與做法,敬望大家批評指正。
一、借助引導性材料,在“教什么”中體現深度
概念是認識事物本質屬性的思維過程,因此有深度的概念教學,應該教以下幾個方面。
1.教如何“由具體到一般,建立認識的一般模式”。概念思維具有一般性和普遍性,今天建立概念的過程與模式既是過去概念建立模式的遷移,又將強化是以后建立概念的經驗。在數列概念之前,筆者先于課前讓學生梳理我們學習函數、集合時是如何學習的,一般內容、模式、步驟是什么,形成了一份表格,然后再呈現新的數列情況。這樣,借助于這種先行組織者,本節課學習的線索、方向就很明確了。同時經數列概念的再次學習,建立概念的一般模式就被再一次強化了。
2.讓學生理解“概念學習的必要性與合理性”。凡是概念的教學,都要讓學生清楚地感受到概念的必要性與合理性。比如本節課,筆者通過設計數列的具體實例情境讓學生感受到數列概念的實際價值,有什么用,也就明白了為什么要定義這個概念。通過讓學生主動參與定義的過程,辨別定義中語句的準確性、嚴謹性,從而感受到概念的合理性:比如,數列概念中“依次”兩個字能否刪除?讓學生去說,讓其他人判斷等等都是要讓學生明白合理性。
為此,本人制作了課前引導性材料,借助于豐富的閱讀材料讓學生去體會,在課堂教學中,再通過問題去促進學生的理解。本節課的課前引導性材料制作如下。
如何認識一類事物?——閱讀材料1
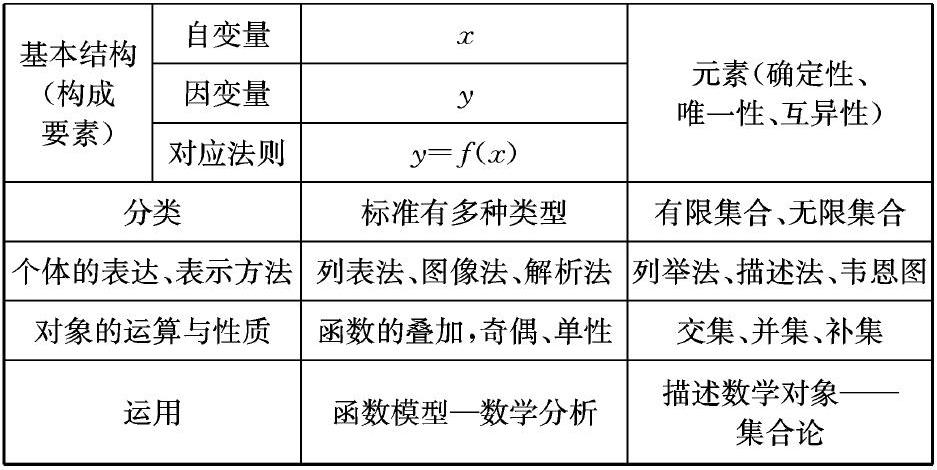
一般說來,研究、學習一個新概念、一類新對象都要關注:它是什么(抽象出一類對象的共同特質、建立概念)——對象命名(類名稱與個體的符號記法)——要素分析(構成元素、基本結構)——外延對象(簡單分類)——每個對象的表達與表現——研究對象(運算,性質)——概念運用。比如我們研究集合與函數的基本線索如下表。
二、設計出好問題,在知識生成過程中體現深度
“問題”是思考的起點,但一個“好的問題”才會引導學生的思考走向深入,為了讓學生在問題的引領下實現深度思考,本人將概念生成的環節分成了三個部分:初步認識、深入認識、反思認識,每個環節都通過具體的問題或者活動激發認知沖突,引導思考爭辯,實現了學生的深度思考。具體環節如下。
(一)初步認識
1.問題引領:這些數列模型有什么共同的特點?你準備從哪些方面來認識?
2.概念的具體化:學生舉例并判斷(概念思維——回到概念)。
(二)深入認識
1.問題1:數列與函數一樣嗎?
2.問題2:數列是一個怎樣的函數?特殊在哪里?準確用自己的語言寫下來。
3.問題3:既然數列是一種特殊的函數,那么從函數的觀點來看數列,你能獲得什么新的認識?
(三)反思認識
問題:數列的項與集合的元素有何區別與聯系?
所有上述問題,除了為了發展出新知識以外,一個重要的目標就是教會學生學會思維,在思維過程中學會思維,正是數學課的重要目的,只有如此,才會有深度。具體說來,包含以下兩個方面。
1.學會“怎樣進行概念的抽象”。既然概念是對事物本質屬性的思維過程,那么概念教學當然就是教“怎樣抽象出事物的本質”,這其中就離不開一般科學的思維:觀察、比較、歸納、抽象、概括與具體化,其中抽象是最核心的環節,它要排除一類對象的所有物理屬性,找到共同的性質,但在完成抽象之前,觀察、比較、歸納是必須的,通過比較異同,找到共性,通過歸納發現共性。抽象出共性以后,還要會表征,用恰當的語言來描述它。在抽象出共性后還要把這個本質推廣到更大的范圍中去檢驗,這就是概括與具體化。因此舉例子就是概念教學的一個重要環節。
2.學會運用概念進行概念思維。李邦河院士曾說,數學是玩概念的,技巧不足懼也,但是玩概念也要會玩,也要有玩概念的意識和習慣。事實上,我們學生之所以曾經會犯錯,就是因為沒有概念思維的習慣與意識,也不會運用概念來判斷、研究問題,或者是不理解內涵,或者是不明確外延,因此教師要指導學生恰當地運用概念、發展概念思維,在數列概念這節課中,讓學生舉一些例子并判斷就是概念思維,通過函數與數列關系,數列項與集合元素辨析就是概念思維。
三、借助于課堂交流,在討論與爭辯中體現深度
深度教學更體現于師生之間、生生之間思維火花的劇烈的碰撞,以及師生之間,生生之間思想的激烈交鋒,深刻意味著能夠給予學生匠心獨用,別有洞天的感慨,意味著喚醒了學生沉睡的思想,意味著啟迪學生的智慧,能夠使學生有醍醐灌頂,柳暗花明,絕處逢生的震撼。要做好這個過程,教師要做好以下幾件事。
1.弄清學生的認知起點與障礙點。本節課中,學生對數列有著豐富的生活體驗,他可能不知道的名詞,他確實做過,解決過與數列相關的實際問題,因此,當豐富的數列是你呈現在眼前時他們不會感到陌生。因此他們也將很快地歸納、抽象出數列的概念——依次排列的一列數。但是關于數列認識的線索卻不盡清楚,即不知道從哪些方面來反映、刻畫數列,因此在課前教師就要提供一個先行組織——函數、集合的學習框架,從而讓學生有線索可循,便于學生主動發展,另一方面,學生也會很容易滿足于數列的一般性描述,對數列的函數本質沒有意識去主動發現因此這是本節課的思維障礙點,為此,筆者特意創設一組問題的辨析讓學生主動發現了數列的函數本質,效果較好。
2.在學生主體與教師主導之間掌握好度。數學是個體再創造的思維過程,沒有個體的主動參與,就沒有思維發生,也就沒有教學的實質。但是也不是事事都要學生探究的,畢竟學習是間接經驗的傳承,關鍵在于掌握一個度,就數列概念這一節課而言,教師要給學生一個認識新對象的方向、順序、一般模式,這是不要探究的,再比如符號記法、簡單分類、要求分析等都可以直接介紹,但概念形成的關鍵部分,比如,數列是什么?數列與函數的關系,數列中的項與集合的元素有何區別都是必須讓學生自己歸納總結,而且必須進行交流、辨析、爭論以形成正確認識的
3.在引導交流、辨析中,指導學生思維與反思。孔子曰:不憤不啟,不悱不發,學生在想說而說不清時,恰當的引導,讓多人辨析、爭論,是彰顯數學火熱思考的重要途徑。在其中對正確的判斷要逼學生解釋原因——為什么這樣呢?不正確的判斷要讓學生舉反例否定,從而發展學生的理性思維,同時學會理性思維的一般模式——正確的要證明,錯誤的要舉反例,這樣學生就具有了邏輯推理能力,同時借助于追問,反詰,也發展了學生反省認知能力,發展了學生理性思維的習慣,最后借助于總結性反思——這節課學到了什么——一類事物的認知方法,從而建立了概念學習的一般模式。
總之,深度意味著悠遠,愛因斯坦說,知識就是當你什么也回憶不出來時所留下的。我想這留下的將是思想,將是說不清、道不明的思維方式,顯然只有深刻,才能久遠,也只有久遠的,才是最有意義的。作為一線教師,我們要不斷努力。
參考文獻:
[1]王玉強.深度教學——構建優質高效課堂的方法[M]. 華東師范大學出版社,2012.
[2]張格波.提升核心素養,我們可以怎樣做?[J].中學數學教學參考,2019(04).
(作者單位:南京市江寧高級中學,江蘇 南京210000)

