亞太GPS/BDS-2/Galileo/GLONASS三頻SPP定位精度分析

李笑笑

(天津城建大學建筑設計研究院有限公司，天津 300000)

我國北斗衛星導航系統是繼美國GPS、歐盟Galileo與俄羅斯GLONASS之后的第四個完全獨立運行的導航系統，與前三者并列全球四大衛星導航系統，建設完成的北斗二號(BDS-2)和北斗三號(BDS-3)都提供高精度導航與定位服務[1-3]。2012年底建設完成的BDS-2主要服務區域為亞太地區，當前BDS-2在軌工作衛星共有16顆，其中6顆GEO衛星、7顆IGSO衛星、3顆MEO衛星，且所有在軌正常工作衛星都播發B1、B2、B3三個頻率，增加了多頻組合定位的多樣性[4-7]。GPS、Galileo、GLONASS雖然不是所有工作衛星都播發三頻信號，但仍能接收到大部分衛星發射的三頻信號，增加多系統多頻組合定位的多樣性。自BDS開始建設以來，很多學者即開展對其本身定位性能、與其他導航系統組合定位性能以及與其他系統定位性能對比分析的研究，胡麗樂等[8]根據多系統組合定位原理提出了一種GPS/GLONASS/BDS/Galileo組合精密單點定位方法，發現四系統組合靜態和動態精密單點定位精度較GPS單系統在E、N、U三個方向提升量在30%～40%之間；李金華等[9]經大量實驗數據分析發現，在極端高度角為45°時，多系統組合的歷元可用率、定位精度、定位的穩定性較GPS單系統都有明顯的提升；朱大勇[10]發現不論是靜態精密單點定位還是動態精密單點定位，在定位精度與收斂時間上較GPS單系統都有明顯的提升；王利華等[11]發現四系統組合動態精密單點定位精度較GPS單系統有明顯的提升，收斂時間較GPS單系統縮短了一半，四系統組合定位較GPS單系統更加穩定，尤其是在高度角較差時最為明顯；劉琳等[12]經研究發現不同系統的單差殘差隨高度角變化呈現不同的特性，除Galileo系統L1、L2觀測值精度相當外，其他系統L1精度要優于L2，同時發現正弦模型和指數模型對GPS和Galileo觀測值精度序列擬合效果較好，而正弦模型對BDS觀測值精度序列擬合效果較差，正弦模型則不適用于GLONASS系統L2精度序列擬合。

鑒于當前對GPS、BDS-2、Galileo、GLONASS三頻組合定位性能的研究較少，因此本文采用三頻無電離層兩兩組合模型處理亞太地區2個IGS跟蹤站實測數據，對比分析了亞太地區GPS、BDS、Galileo、GLONASS三頻單點定位(Single Point Positioning)定位精度。

1 單系統SPP模型

單系統SPP定位觀測方程可以表示如下[13-15]:

(1)

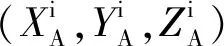
在式(1)的基礎上可以進一步得到三頻兩兩無電離層組合模型為：

(2)

(3)

設測站坐標為(x0,y0,z0)，在此處按照泰勒級數展開，即可得到誤差方程如下：

(4)

式中，n為衛星數；(δx,δy,δz)為測站坐標改正數；a,b,l為測站至衛星視線向三個方向余弦值；L為常數項。

在式(4)的基礎上，進一步利用卡爾曼濾波進行參數估計以及最小二乘算法求解，即可解算得到測站坐標。

2 數據解算分析

2.1 數據源

為詳細分析亞太地區GPS、BDS-2、Galileo、GLONASS三頻SPP定位精度，選用位于亞太地區的IGS連續跟蹤站CUT0站和YARR兩個觀測站，所選測站均位于澳大利亞境內，觀測時間為2020年5月12日00:00:00～24:00:00，采樣間隔為30 s。采用根據RTKLIB編譯實現的程序進行數據處理，對GPS、BDS-2、Galileo、GLONASS三頻數據衛星可見數、PDOP值以及三頻SPP定位精度進行分析。

2.2 解算結果分析

鑒于當前GPS、BDS-2、Galileo、GLONASS在軌正常工作衛星數各不相同，首先分析亞太地區四個系統能播發三頻數據的衛星可見數與PDOP值(即衛星空間幾何構型)，圖1和圖2分別給出了四個系統衛星可見數與PDOP值的對比。通過圖1可以發現，在整個時段內，BDS-2的衛星可見數變化范圍優于GPS優于Galileo和GLONASS，而Galileo衛星可見數變化范圍與GLONASS相當，其中GPS平均衛星可見數為9顆，BDS-2平均衛星可見數為10顆，Galileo平均衛星可見數為6顆，GLONASS平均衛星可見數為6顆。通過圖2可以發現，在整個時段內，GPS系統PDOP值變化范圍小于BDS-2、Galileo和GLONASS，BDS-2、Galileo和GLONASS系統PDOP值變化范圍相當，GPS平均PDOP值為1.91，BDS-2平均PDOP值為2.52，Galileo平均PDOP值為2.62，GLONASS平均PDOP值為2.60。

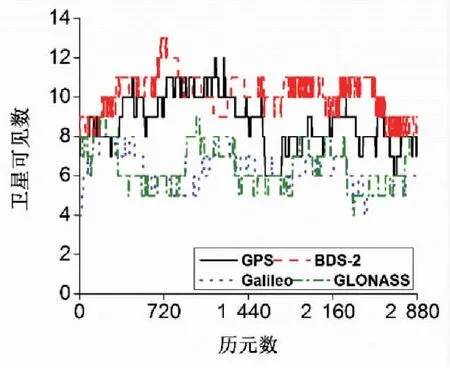
圖1 不同系統衛星可見數對比

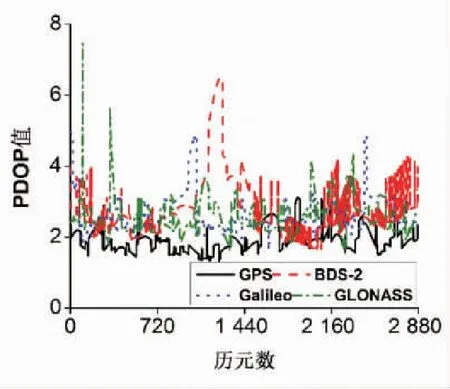
圖2 不同系統PDOP值對比

在進行數據處理時，以所選測站IGS周解算坐標值作為參考值，將解算得到四個系統三頻組合SPP所有歷元的坐標值與參考值做差，得到所選測站X方向、Y方向、Z方向定位誤差序列如圖3和圖4所示。通過圖3可以發現，對于CUT0站四個系統SPP定位誤差，在X方向，GPS和BDS-2定位誤差在±3 m范圍內波動，Galileo定位誤差在±6 m范圍內波動，GLONASS定位誤差在±4 m范圍內波動；在Y方向，GPS和BDS-2定位誤差在±2 m范圍內波動，Galileo定位誤差在±4 m范圍內波動，GLONASS定位誤差在±6 m范圍內波動；在Z方向，GPS、BDS-2、Galileo定位誤差在±9 m范圍內波動，GLONASS定位誤差在±12 m范圍內波動。

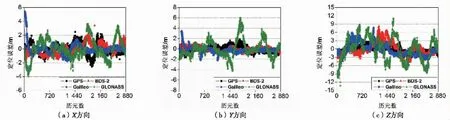
圖3 CUT0站GPS、BDS-2、Galileo、GLONASS三頻SPP定位誤差序列

通過圖4可以發現，對于YARR站四個系統SPP定位誤差，在X方向，GPS和BDS-2定位誤差在±2 m范圍內波動，Galileo和GLONASS定位誤差在±4 m范圍內波動；在Y方向，GPS和BDS-2定位誤差在±2 m范圍內波動，Galileo定位誤差在±8 m范圍內波動，GLONASS定位誤差在±6 m范圍內波動；在Z方向，GPS和BDS-2定位誤差在±6 m范圍內波動，Galileo定位誤差在±15 m范圍內波動，GLONASS定位誤差在±14 m范圍內波動。

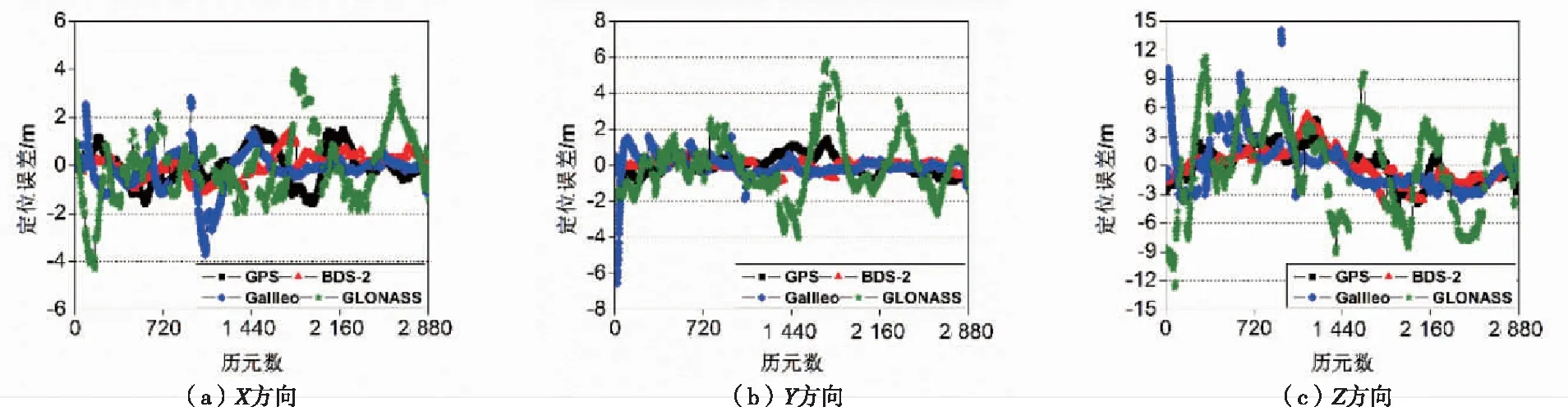
圖4 YARR站GPS、BDS-2、Galileo、GLONASS三頻SPP定位誤差序列

根據計算得到的四個系統X方向、Y方向、Z方向定位誤差，進一步統計X方向、Y方向、Z方向、3D方向的定位精度(RMS值)，如表1所示。

通過表1可以發現，GPS、BDS-2、Galileo三個系統三頻SPP定位X方向和Y方向定位精度優于1 m，GLONASS系統三頻SPP定位X方向和Y方向定位精度優于2 m，GPS、BDS-2三頻SPP定位Z方向定位精度優于2 m，Galileo三頻SPP定位Z方向定位精度優于3 m，GLONASS三頻SPP定位Z方向定位精度優于5 m，對于3D方向四個系統的定位精度關系為：BDS-2>GPS>Galileo>GLONASS，這與四系統的衛星可見數與PDOP值有一定關系。進一步計算兩個測站四個系統3D方向定位精度平均值，計算BDS-2三頻SPP定位精度較GPS、Galileo、GLONASS三個系統三頻SPP定位精度的提升，BDS-2三頻SPP定位精度較GPS系統三頻SPP定位精度高8.59%，較Galileo系統三頻SPP定位精度高38.12%，較GLONASS系統三頻SPP定位精度高97.53%。

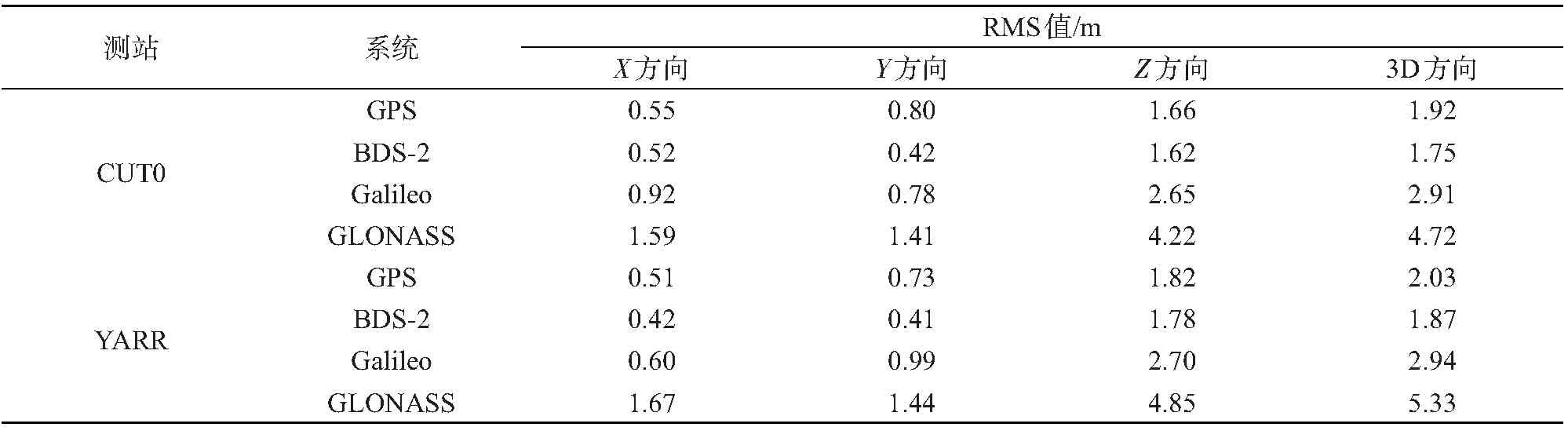
表1 四系統三頻SPP定位精度統計

3 結 語

本文基于亞太地區IGS連續跟蹤站多模多頻實測數據，對比分析了亞太地區GPS、BDS-2、Galileo、GLONASS四個系統三頻組合SPP定位精度，經分析發現，在亞太地區，BDS-2的衛星可見數最多，但GPS衛星空間幾何結構最優，Galileo與GLONASS的衛星可見數與衛星空間幾何結構相當，BDS-2三頻SPP定位精度最優，其次為GPS系統和Galileo系統，GLONASS系統相比其他三個系統定位精度最差，可為今后亞太地區定位系統選擇上提供一定的參考。