淺談小學數學開放性應用題的命制和評價

劉小會

【摘要】新課程理念強調：為了適應時代發展對人才的需要，數學課程需要特別注重發展學生的應用意識和創新意識.本文以三道小學數學開放性應用題為切入點，探討這類題型的命制和評價.開放性應用題應源于教材，又不拘泥于教材.與其他應用題相比，開放性應用題更具靈活性、開放性和綜合性，更能培養學生的應用意識和創新意識.

【關鍵詞】開放性; 魔方; T字之謎;找規律

一、玩轉五階魔方，提升空間觀念

在三維空間中，以邊長為1 cm的正方體為基本構建塊，組成我們熟悉的五階魔方.通過設置不同的情境，分別求解該五階魔方的體積和表面積.本題以小學生喜聞樂見的魔方為背景，把學生的認知水平由幾何直觀上升到空間想象和空間推演.問題梯度由易到難，層層遞進.本題適用于五年級下學期及以上學段的學生.

正題：邊長為1 cm的正方體組成一個五階魔方：

（1）求出該五階魔方（圖1（a））的體積和表面積.

（2）如果在魔方內部摳掉一部分正方體，即打通魔方，形成5個洞，如圖1（c）所示，求剩下部分的體積和表面積.

（3）在圖1（c）的基礎上，再摳掉最上面正中心處的方塊（打通形成第6個洞，如圖1（d）所示），求剩下部分的體積和表面積.

評價參考標準及建議：

（1）體積：5×5×5=125（cm3）.

表面積：5×5×6=150（cm2）.

評價細則：這一問不難，可以利用公式求出五階魔方（邊長為5 cm的正方體）的體積和表面積.

（2）體積：125-5×5=100（cm3）.

表面積：150+5×5×4-5×2=240（cm2）.

評價細則：①在第一問的基礎上，用總體積減去摳掉部分的體積即可.5×5表示5個洞總共被摳掉的小正方體的數目.②5×4表示1個洞中魔方內部所增加的面數，5×5×4表示5個洞中魔方內部所增加的面數，5×2表示魔方表面減少的面數.

（3）體積：100-4=96（cm3）.

表面積：240+4×4-2-2=252（cm2）.

評價細則：①在第二問的基礎上，用總體積減去摳掉部分的體積即可.4表示第6個洞被摳掉的方體數目.為什么是4而不是5呢？因為第6個洞和原來的一個洞在一個方塊處交匯，所以這里不能重復計算.②此時這個問題已經比較復雜了，并且層層遞進.在第二問所求表面積的基礎上，解答此問的表面積.4×4表示第6個洞中，魔方內部（4個方塊）所增加的面數，第一個2表示魔方表面減少的面數，第二個2表示交匯處減少的面數.

二、巧解T字之謎，探尋組合奧秘

本題屬于數學好玩的范疇，以民間智慧“T字之謎”為數學背景，探討組合圖形的構造、面積計算和形狀多樣性等問題.類似于七巧板，“T字之謎”也屬于智力拼板玩具，但只有四塊，所以也稱“四巧板”，與七巧板性質相同.“T字之謎”的組合過程著重考查觀察能力、動手能力和銜接能力.本題適用于五年級下學期及以上學段的學生，重在開拓思維和發散想象，答案具有多樣性和開放性.

正題：“T字之謎”由四塊不同形狀的單元塊組成：一個等腰直角三角形①、一個不規則五邊形②、一個短直角梯形③、一個長直角梯形④.如圖2所示.

（1）把這四個單元塊組合成“T”字，畫出示意圖，并計算總面積.（2）計算不規則五邊形②的面積.

（3）“T字之謎”中的四塊單元塊還可以組合成其他圖形嗎？請列出兩種形狀.

評價參考標準及建議：

（1）四塊單元塊拼接成兩個長方形，組成“T”字.“T”字如圖3（1）所示.對應的T字面積：1×3+1×3=6（cm2）.

（2）不規則五邊形②的面積計算如下：

方法一：②的面積=T的面積-①的面積-③的面積-④的面積=6-0.5-1-2.5=2（cm2）.

方法二：把五邊形分割成一個平行四邊形和一個三角形，如圖3（2）所示.根據第一問中“T”字的組成形式，得出平行四邊形的高和三角形的底.

②的面積=1.5+0.5=2（cm2）.

（3）此問具有開放性，答案不唯一.組合的關鍵在于把長度相等的邊拼接在一起.圖4中展示了6種形狀，方法多樣，巧妙有趣.事實上，目前“T字之謎”的拼湊有上百種情況，是老少皆宜的休閑智力玩具.

三、構造方形串聯，挖掘潛在規律

本題利用分割法、觀察法和找規律法解決求復雜圖形面積的問題.學生體驗圖形形狀變化與面積大小變化關系的同時，通過猜想和歸納找到形與數之間的關系.本題適用于五年級下學期及以上學段的學生.

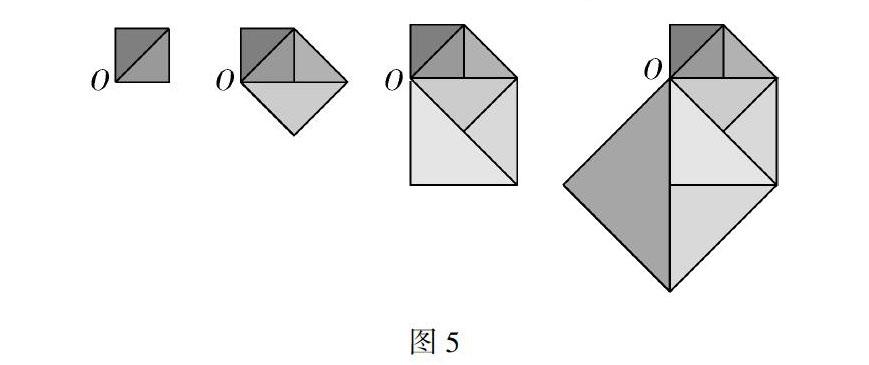
正題：從邊長是1 cm的正方形開始，從O點出發，以正方形的對角線為邊順時針連續畫正方形，如圖5所示：

（1）畫出第5個正方形，并求出邊長.

（2）用兩種不同的方法求畫第5個正方形時所得圖形的總面積.

（3）綜合5幅圖，在計算圖形總面積的過程中，你可以找到一些規律嗎？

評價參考標準及建議：

（1）畫出第5個正方形，如圖6（1）所示，邊長為1×4=4（cm）.

評價細則：以第4個正方形的對角線為邊，畫出第5個正方形.通過觀察，發現此時的邊長為4個1 cm.

（2）面積計算參考方法（不限）如下：

方法一：圖形可以分割成如圖6（2）所示的三部分，分別計算求和即得總面積.

面積=①+②+③=1.5+6+16=23.5（cm2）.

方法二：圖形可以分割成如圖6（3）所示的47個完全一樣的小三角形.

面積=47×0.5=23.5（cm2）.

（3）參考答案見表格.

這個規律有點類似于斐波那契數列，利用前一類信息，計算下一類信息.文字描述如下：

后一個圖形三角形的個數=前一個圖形三角形的個數×2+1，對應數學表達式為：f（n+1）=2f（n）+1，f（1）=2，f（n）=3×2n-1-1.

四、結束語

開放性應用題的探討就像一段旅行，其終點不是讓學生獲得一堆零散、呆板和固定的知識，而是讓他們能夠積極、充分、靈活地運用數學知識去發散思維、解決問題并且學以致用，由此獲得人格的健全和精神的成長，成為新時代的社會主義建設者和接班人.此外，應用意識和創新意識的培養應該從義務教育階段做起，并貫串于數學教育的始終.