基于FPGA 的高頻電力電子裝置快速實時仿真數值算法

施 文，遲 頌，郭 亮

（1.河北工業大學電氣工程學院省部共建電工裝備可靠性與智能化國家重點實驗室，天津300132；2.河北工業大學電氣工程學院河北省電磁場與電器可靠性重點實驗室，天津300132）

以實時仿真為核心的數字雙胞胎技術，能夠幫助企業在實際投入生產之前在虛擬環境中優化、仿真和測試，實現高效的柔性生產，是企業邁入工業4.0 的解決方案之一， 然而由于寬禁帶器件的高頻特性使得電力電子裝置與數字雙胞胎結合的難度增加。 寬禁帶器件開關頻率可達百kHz，最小穩態時間可低于1 μs，而常見的基于現場可編程門陣列FPGA（field programmable gate array）實時仿真平臺RT-LAB、PXI 平臺等仿真步長在250 ns 到1 μs 之間[1-2]。過高的開關頻率會使得仿真中出現開關時刻偏移等問題，一般采用變步長計算。

文獻[3-5]提出了實時仿真并行化的方法，證明了在并行化實時仿真中，可以異步仿真，無須考慮與通訊部分同步， 每部分仿真模型可以將仿真步長減小至算法極限。因此，減少仿真計算時間可以減小仿真步長，有助于在高頻下簡化開關動作情況，提高仿真精度。算法方面，文獻[6-7]利用多步插值的變步長算法，解決了多重開關動作的問題，但算法復雜難以實時計算；文獻[8]比較了常用離散迭代算法仿真精度，證明了梯形法綜合性能更優；文獻[9]使用權重數值積分的方法解決了變步長仿真中的數值發散問題，但都沒有涉及實時仿真；文獻[10]通過單步插值實現了實時仿真變步長算法；文獻[11]通過二階段積分和自校正單步插值的方法解決了變步長的相關問題，但都未考慮計算時間對仿真步長的影響。

針對現有實時仿真中使用的變步長算法計算速度和數值發散的問題，提出一種基于FPGA 程序結構的實時仿真數值算法，通過改進梯形迭代法以提高算法收斂程度， 在此基礎上改進仿真算法結構，使計算更加快速穩定。以三相逆變電路為例，以離線仿真軟件精度為標準，對改進算法進行實時仿真，證明算法的有效性。

1 高頻電力電子實時仿真存在問題

隨著電力電子系統開關頻率的不斷提高，仿真中會出現開關動作時刻與采樣點時刻不一致的情況， 這時開關動作時刻會被歸算到采樣點時刻，出現開關動作偏移的問題。一般采用變步長算法進行處理，但隨之帶來了關于數值發散[11]與實時性的問題。 文獻[12]總結了變步長算法及適用情況，文獻[13]對開關動作偏移問題進行了詳細的描述。

（1）數值發散的問題。 由于步長過大或者算法精度不足導致仿真結果發散，通常可以使用高階迭代算法、多步迭代等方法解決，但在實時仿真中會增加計算時間，進而增大步長，使問題更加復雜，甚至無法保證實時。

（2）實時性問題。 實時仿真最重要的是滿足實時性，即：①實時性，步長設定時間等于數據傳輸間隔時間；②穩定性，最長仿真計算時間小于步長設定時間。

常用的高階迭代算法會增加總體仿真計算時間，變步長仿真中采用半步長歐拉法仿真增加最長仿真計算時間，從而變相增大了步長。

本文在實時仿真變步長算法的基礎上，針對問題（1）提出改進的梯形法以提高收斂性，在此基礎上針對問題（2）改進算法計算結構，使計算更加穩定快速，可使仿真步長進一步減小。

2 基于系數控制的數值解算方法

2.1 改進的梯形迭代算法

一般實時仿真主要使用歐拉法迭代配合狀態方程對離散電路模型進行求解，公式表示為

其中：第1 式為狀態方程，第2 式為歐拉法公式。式中：h 為仿真步長；X 為狀態變量；為狀態變量的導數；A 和B 為狀態方程的數值矩陣； 下標n 代表離散時間點。

歐拉法精度較低， 仿真結果易出現數值發散，可以使用梯形法來提高精度[8-9]。 同樣對于狀態變量的導數求解使用狀態變量法，梯形迭代法公式為

式中，X'為對下一時刻狀態變量的預測值。 在實時仿真中，預測計算會延長仿真計算時間，導致仿真步長增大。 通過圖1 進行說明。

圖1 梯形迭代法計算流程Fig. 1 Calculation flow diagram of trapezoidal iterative algorithm

圖1 為梯形迭代法的簡化計算流程，其中細箭頭表示常數乘法，1/2 表示系數數值，未寫數值則系數為1； 而粗箭頭代表狀態方程AX+B 的計算，最為消耗計算時間，省略了步長h 乘法計算。 梯形迭代法會進行2 次狀態方程計算， 存在時序問題，無法并行計算。相比于歐拉法，計算時間增長近1 倍。

為了減少計算時間，對梯形法進行一定改進。圖1 中，tn到tn+1中第一次狀態方程的計算結果，與tn-1到tn的基于歐拉法的預測計算結果在一定條件下近似等效。 將替換為，可以節省一次狀態方程計算，改進的梯形迭代法計算流程如圖2 所示。

圖2 改進的梯形迭代法計算流程Fig. 2 Calculation flow diagram of improved trapezoidal iterative algorithm

梯形迭代法從tn-1到tn的仿真計算中，存在使用歐拉法對tn的狀態變量導數進行預測計算結果，將其運用在tn對tn+1的仿真計算中，如圖2 虛線部分所示，整理后得到

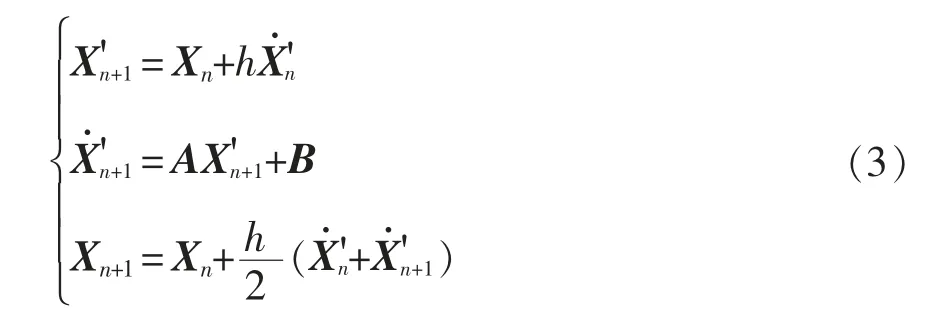
相對于傳統梯形迭代法，改進迭代法計算省去一次狀態方程的計算，速度更快。

精度方面， 以buck 電路為例對比算法誤差進行說明。 電路拓撲如圖3 所示。 其中，Es為電源電壓，取100 V；電感L 為0.1 mH；負載電阻Rload為2.5 Ω；占空比取0.5；開關頻率為10 kHz。對比歐拉法、 改進梯形法與梯形法低步長的仿真結果，以PLECS 仿真結果為標準，計算誤差[14]公式為

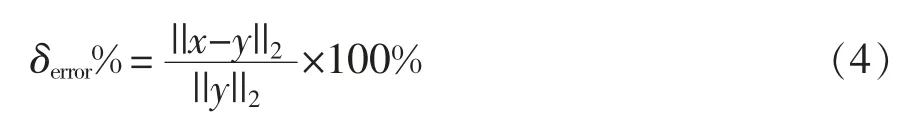
式中：δerror為相對范數誤差；x 為標準結果；y 為對比數據。 誤差曲線如圖4 所示。

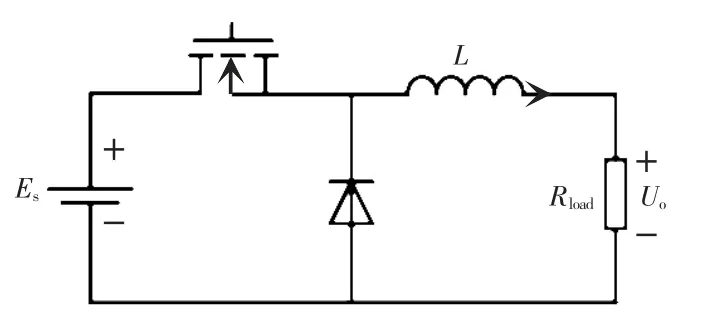
圖3 Buck 電路拓撲Fig. 3 Topology of buck circuit

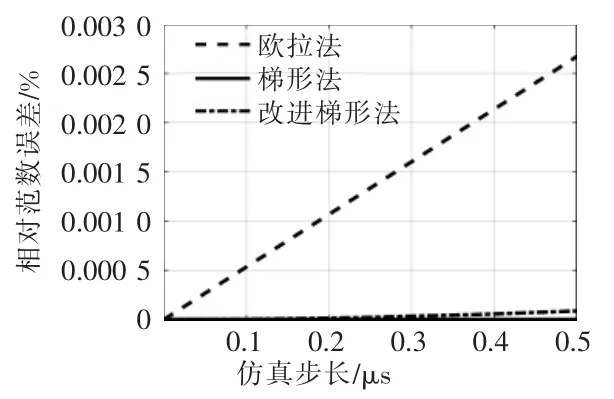
圖4 buck 電路輸出電壓誤差曲線Fig. 4 Error curves of buck circuit output voltage

表1 給出了本算例中不同算法預計計算時間，其中計算按1 個時鐘周期（clk）計時（使用定點數計算），開關判斷為1 clk，并行計算時間為最長路徑計算時間。

仿真精度方面， 改進梯形法與梯形法相近，都遠小于歐拉法；在計算時間方面，相較于梯形法，改進梯形法時間約減少了45.5%。

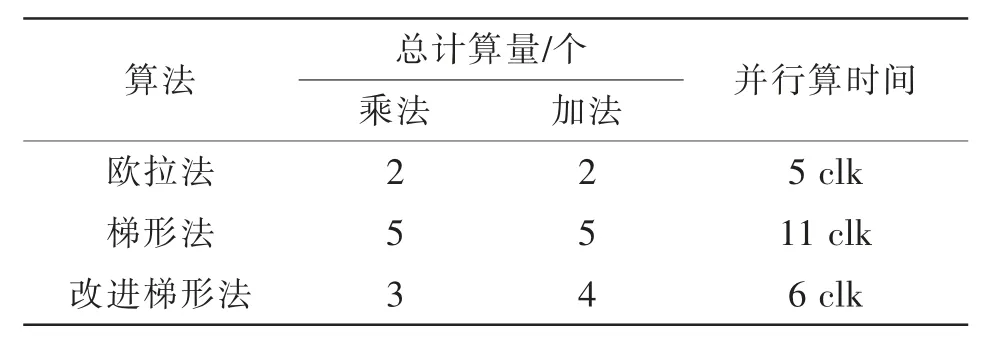
表1 不同算法預計計算時間Tab. 1 Computation time predicted using different algorithms

2.2 變步長算法計算步驟

文獻[10]中的變步長算法，在完成插值后，將步長調整為原步長的一半， 使用歐拉法迭代計算2次，以此提高收斂性與計算精度，但在變步長時刻需要進行2～3 次迭代計算，仿真時間較長。 為加快計算速度，改進了變步長算法計算步驟[12]，計算流程如圖5 所示。

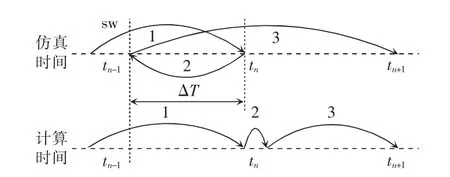
圖5 改進的變步長算法計算流程Fig. 5 Calculation flow diagram of improved variablestep algorithm

步驟1從tn-1到tn時刻進行計算， 并檢測到開關動作；

步驟2對狀態變量插值，將狀態還原到開關時刻tsw；

步驟3步長變為h+ΔT 進行仿真計算， 仿真時間與計算時間相等，保證實時性。

步驟2 和步驟3 對應的計算公式為

式中，ΔT 為圖5 中對應的時間間隔。

在圖5 計算過程中， 經過了2 次仿真計算，完成了2 個步長的仿真計算，可以保證每個步長只進行一次迭代計算，仿真計算時間穩定，單步長內計算快速。

2.3 改進的實時仿真數值計算方法

同時使用改進的梯形法、歐拉法、改進的變步長算法可以完成變步長計算，保證變步長計算中仿真結果的收斂性。 3 種方法都只進行一次矩陣乘法，計算速度相近，計算快速。

但由于FPGA 屬于分布式處理器，每多一種情況都要預留相應的計算資源，同時使用3 種算法使FPGA 程序實現的難度提升， 因此需要對3 種算法（式（1）、式（3）、式（5））的計算結構進行改進，減少不同的計算分支。參考權重數值積分[9]的方法，將權重轉變為幾個確定的系數，通過控制系數進行計算[10]，將算法的選擇轉變為系數的選擇，提升FPGA 程序效率。

以式（5）變步長算法的計算結構為原型，進行算法結構的改進；式（3）的改進梯形法與變步長算法結構相近，不做調整；式（1）歐拉迭代法向式（5）計算結構進行靠近，對式（1）進行擴充，增加2 個0系數的部分， 并將過程量等效為梯形法中的相等量，使計算結構靠近式（5），最終得到

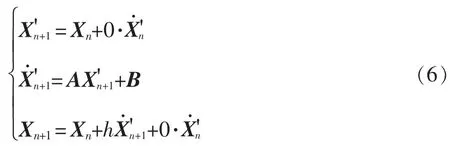
對式（6）、式（3）、式（5）相同部分進行提取，不同部分使用系數a、b、c 代替得到

系數a、b、c 的不同取值及其對應的算法如表2所示。 計算步驟如下。

步驟1通過開關動作采樣程序， 得到上一個步長中的開關動作情況，即是否開關動作和動作時間點ΔT。

步驟2根據步驟1 中開關動作情況進行系數的選擇，選擇原則如下：

（1）判斷開關是否動作。若開關未動作，使用改進梯形法；若開關動作，進入下一步判斷。

（2）判斷開關動作時間點ΔT。若ΔT>0，使用變步長算法；若ΔT=0，使用歐拉法。

步驟3根據選擇的系數進行之后的計算。

除了只進行一次矩陣乘法計算快速外，與切換算法相比， 切換系數對FPGA 的資源占用減小很多，便于程序編寫與仿真系統的建立；與使用多種算法相比，改進的算法計算結構在每個步長中的計算量一定，計算時間穩定，易于與通信程序和采樣程序配合。

表2 不同算法對應系數設置Tab. 2 Coefficient settings of different algorithms

3 仿真算法FPGA 程序結構

3.1 實時仿真算法的FPGA 程序結構

FPGA 程序硬件設計結構如圖6 所示，圖中，實線部分為原有歐拉法定步長算法，虛線部分為本文算法增加部分，最下方為時間軸；圖6 為一個步長中涉及的計算，計算模塊是考慮并行運算的基礎上根據計算的時間先后順序進行排列，仿真計算時根據從左到右的順序進行計算（對應時間軸相同即為并行運算）。

虛線部分改進主要體現在以下3 個方面：

（2）與系數a 相關的算法切換與數值補償部分，可以與矩陣計算同時進行，不增加計算時間；

（3）與系數b 相關的控制步長變換部分。

與傳統的定步長歐拉法計算對比，核心的矩陣計算時間不變，最長計算路徑增加2 個乘法與1 個加法。僅需提取開關信號并對狀態變量進行處理即可，不需要對算法進行根本的改動，便于對已有程序的結構進行升級與優化。

如圖6 所示，在資源使用方面，增加計算資源主要針對狀態變量的數量，正比于狀態方程矩陣階數；而整體計算資源近似正比于狀態方程矩陣階數二次方，即隨著矩陣階數增大，增加計算資源所占比例將逐漸減小。

圖6 FPGA 程序硬件結構設計示意Fig. 6 Schematic of FPGA program hardware structure design

3.2 實時仿真算法的FPGA 程序結構

由于仿真所選拓撲不同、硬件不同，仿真時間不確定。 為保證對比簡潔，以第2.1 節中的算例為例進行分析。 如圖5 所示，變步長的插值算法需要增加1 個乘法與1 個加法。以算例中的并行計算方式統計預計計算時間，如表3 所示。

在本算例中，計算時間可以節省72%，由于本文算法所占據的時間可并行，不隨矩陣階數增加而增加，節省時間比率相對穩定。

表3 不同算法的計算時間Tab. 3 Computation time of different algorithms

4 實時仿真平臺實驗驗證

4.1 仿真程序實驗平臺

本文使用的FPGA 開發板為Arria II GX 系列開發板，芯片型號為EP2AGX125EF35。 該FPGA 開發板提供124 100 個邏輯單元、576 個18×18 DSP乘法器，并配置頻率100 MHz 晶振器，可以提供足量的計算資源。

實驗數據通過Altera 公司的開發套件Quartus Prime 中SignalTap II 程序， 設置探針程序對FPGA仿真結果進行數據提取。

4.2 實驗用仿真模型

仿真電路采用三相逆變器接LC 濾波器帶對稱阻感負載，電路拓撲如圖7 所示，為方便程序計算規定點o 為參考節點。 電路模型使用狀態變量法。開關模型方面， 開通等效為電壓源串聯電阻模型（見圖7 中虛線），關斷等效為開路。 仿真電路參數如表4 所示。

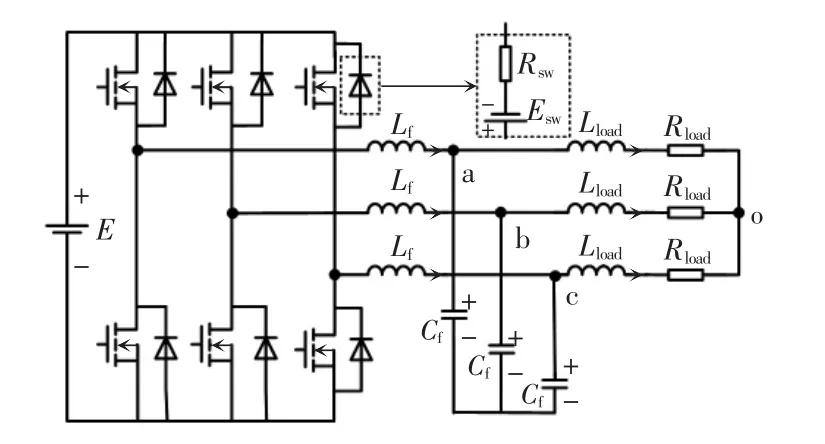
圖7 三相逆變器電路拓撲Fig. 7 Topology of three-phase inverter circuit

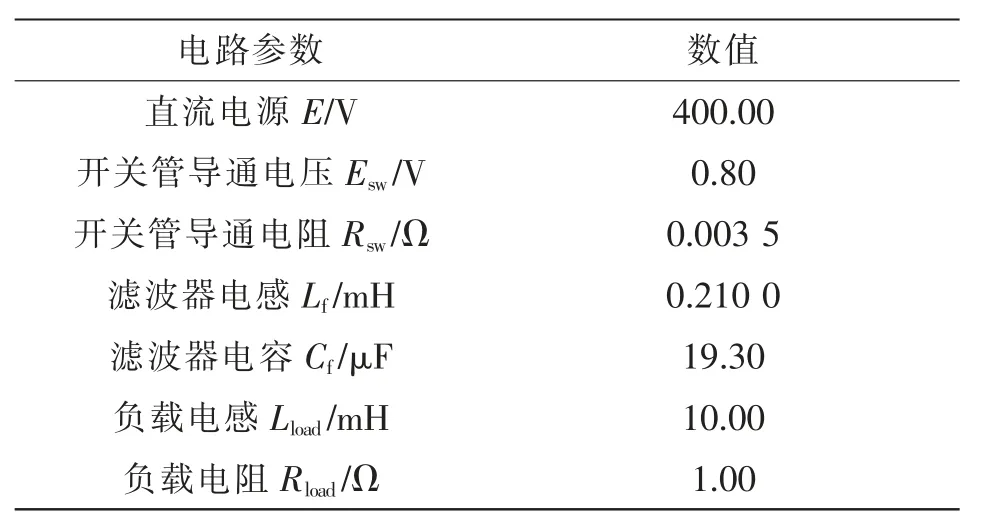
表4 仿真電路參數數據Tab. 4 Data of simulation circuit parameters

控制采用雙極性正弦脈寬調制SPWM（sinusoidal pulse width modulation）控制，正弦波通過直接數字頻率合成DDS（direct digital frequency synthesis）技術[15]將正弦波離散化后存入存儲器中，根據仿真步長調用數據。 受開發板存儲限制，為保證控制信號足夠精確，排除控制不同帶來的誤差，輸出設定為基頻250 Hz 的三相正弦波，LC 濾波器的截止頻率按照10 倍基頻整定。

算例主要使用定點數的數值進行計算，本文算法計算使用時間為130 ns，步長設定在130 ns 以上即可保證實時性。 控制信號周期與步長同步，開關頻率取110 kHz。

4.3 仿真結果對比與分析

4.3.1 算法收斂性驗證

為便于觀測發散現象，避免算法諧波誤差與數值發散的結果疊加，步長采用本文算法500 ns 與歐拉法500 ns 進行仿真，仿真結果如圖8 所示。 本文在計算時間方面與歐拉法相當，而在同樣步長500 ns 情況下， 本文算法的輸出波形是正常的正弦波形，而歐拉法出現了明顯的數值發散情況。

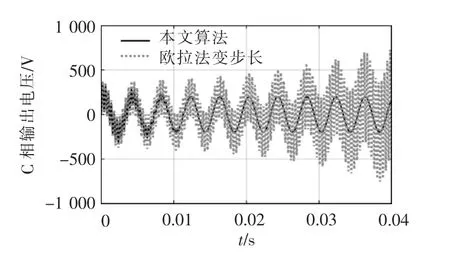
圖8 不同迭代算法的仿真結果比較Fig. 8 Comparison of simulation results between different iterative algorithms

4.3.2 算法仿真驗證

由于并行仿真無需預留過多通信時間，仿真步長可以接近計算時間， 算例中設置步長為150 ns，大于計算時間130 ns，滿足實時性。 圖9 為本文算法步長150 ns 下，三相逆變器的三相輸出電壓（圖7 中為A 相uao、B 相ubo、C 相uco）與三相輸出電流（圖7 中為A 相iao、B 相ibo、C 相ico）。

由圖9 可見， 逆變器輸出電壓和輸出電流為平滑的三相正弦曲線，無諧波影響，本文算法的變步長部分計算正常，算法收斂性正常。仿真結果證明了算法的有效性。 將圖9 中的計算結果與PLECS 軟件變步長計算結果作對比，以A 相輸出電壓和輸出電流為例，結果如圖10 所示。使用式（4）對圖9 的三相輸出結果進行誤差計算，計算結果如表5 所示。

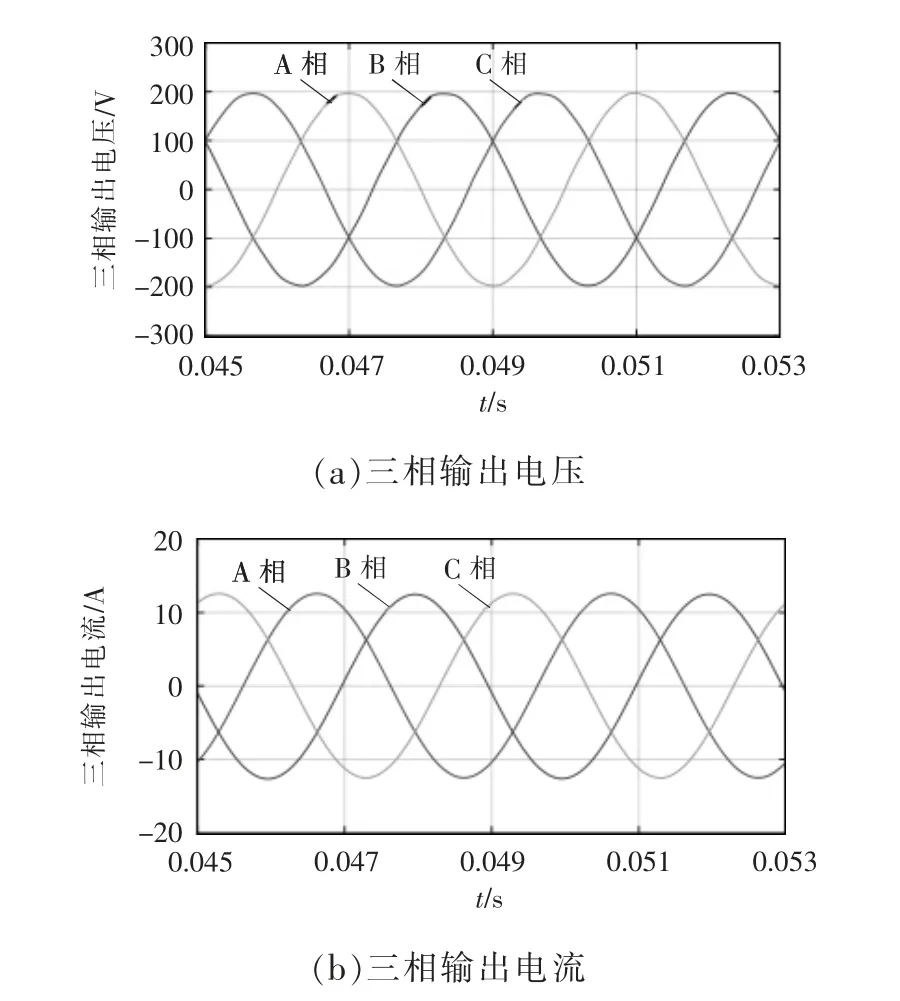
圖9 三相逆變器輸出波形Fig. 9 Output waveforms of three-phase inverter

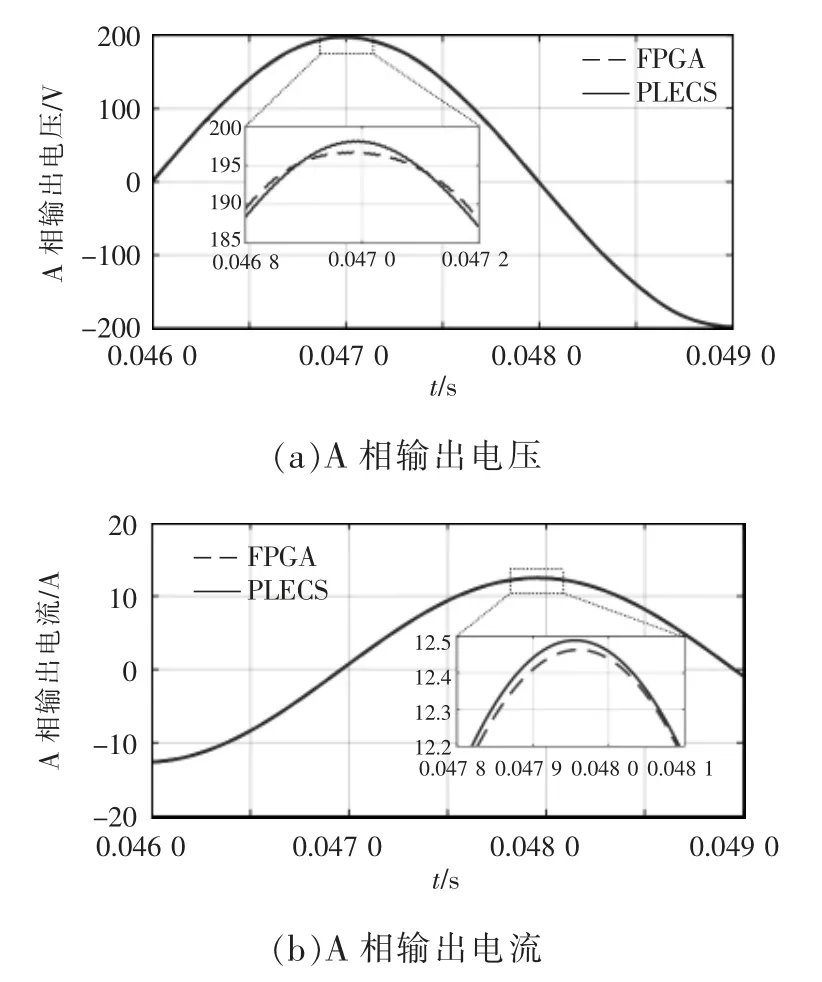
圖10 A 相輸出波形對比Fig. 10 Comparison of output waveform in phase A

表5 實時仿真結果誤差Tab. 5 Errors of real-time simulation results

結果表示誤差較小，仿真結果可用。 算法計算時間為130 ns，與一次歐拉法計算時間相近，而使用半步長歐拉法進行變步長計算，需要約3 倍的歐拉法計算時間。與之相比，本文算法可以節省約2/3的計算時間，而由于計算快速，步長較小，誤差可以進一步減小。

5 結論

針對變步長實時仿真給嵌入式實時仿真帶來的數值發散和計算時間不穩定的問題，提出一種基于FPGA 程序結構的實時仿真算法，優勢為：①計算時間穩定；②收斂快且計算快速，相較于梯形法，計算時間減少近一半；③仿真精度方面，與梯形法相近，但遠小于歐拉法。

穩定的計算時間有助于通信程序的設置與實時仿真模塊之間的數據交互，而快速計算可以減小步長，有助于降低多重開關事件的出現，降低仿真計算難度。

算例中使用100 MHz 晶振的FPGA 開發板，如使用RT-LAB 等實驗級FPGA 開發板，仿真速度還可進一步提升。后續將研究實驗級FPGA 開發板對仿真速度的提升情況，進一步探究步長減小與電力電子仿真開關頻率提升程度的具體關系。