LED 驅動電路超高次諧波發射機理研究
朱明星,張曉剛
(教育部電能質量工程研究中心(安徽大學),合肥230601)
據高工產研鋰電研究所GGII 調研數據顯示,2014 年LED 全球通用照明市場為807 億美元,2015 年為849 億美元,同比增長5.2%,預計2019年LED 全球通用照明市場規模將突破1 000 億美元,2014—2019 年年均復合增長率為5.3%。LED 行業作為我國重點扶持的行業,市場規模也在不斷擴大, 其中LED 通用照明作為LED 各應用行業中最主要的市場,近七年復合增長率高達59.4%。
LED 具有工作電壓低、 壽命長和能耗低的特征,已被廣泛運用到照明和背光等領域。 常用LED驅動電路分為: 電阻限流驅動、 線性驅動和開關驅動。其中開關驅動電路能效轉換最高、輸出電壓電流穩定,在LED 驅動電路中占比最多。 開關驅動是一種通過高頻開關方式來進行電能轉換的低功耗驅動電路,在工業控制及家電領域得到了普遍使用[1]。 隨著越來越多新型電器設備接入電網,向電網注入的2~150 kHz 超高次諧波越來越多,由此造成的電磁干擾問題將會不斷增多,產生的危害也勢必越發嚴重[2]。 在2013 年電氣與電子工程師協會IEEE(Institute of Electrical and Electronic Engineers)電力與能源國際會議上首次將電力系統電壓電流中的高頻成分定義為超高次諧波(supraharmonics)。 當前,國內外對電器自動化設備電力電子化伴生的超高次諧波電能質量問題進行了一些測試和仿真分析,但仍處于起步階段[3-7]。
文獻[8]對光伏逆變器、風機變頻器、電動汽車充電樁等典型超高次諧波源的特點進行了梳理和歸納,并結合傳統電能質量概念,從頻域、時域、時-頻域給出了超高次諧波發射標準的一些建議指標;文獻[9]對電動汽車充電樁變流器的網側諧波發射特性進行了分析,通過仿真給出了變流器網側超高次諧波的頻譜分布規律,并說明了載波頻率對超高次諧波的影響,但未究其原因作出相應論述;文獻[10]主要對現有超高次諧波測量、分析方法和標準進行了比較,并對超高次諧波的一次發射和二次發射進行了分析,提出了幾種估算超高次諧波貢獻度的思路;文獻[11]通過大量的測量和分析,歸納出了低壓電網中超高次諧波的產生原因和傳播特性,但文章僅對電網中超高次諧波源進行了分類,缺少對諧波源內部工作原理的研究。
已有研究中通常僅關注超高次諧波源的外部發射特性,而對超高次諧波的產生原因及相關影響因素的理論分析鮮有涉及。本文通過對電流控制模式LED 開關驅動電路在不同工作狀態時的數學建模與仿真研究,詳細分析其超高次諧波產生機理及影響因素。
1 電流控制模式LED 驅動電路分析
1.1 電流控制模式LED 驅動電路拓撲
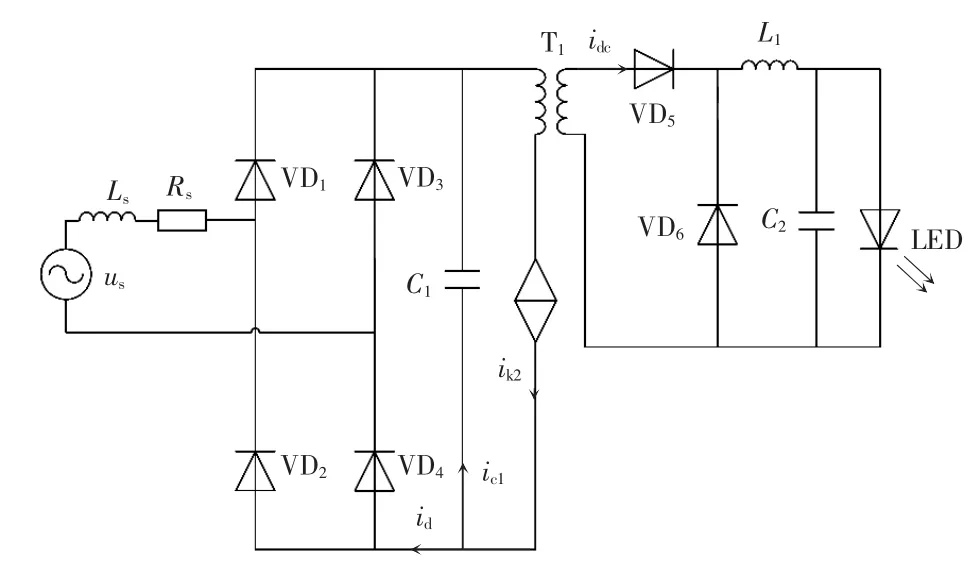
常見的開關驅動電路有推挽式、正激式、反激式和電荷泵等多種電路結構。不同電路結構在采用不同控制策略后又可分為電壓控制模式和電流控制模式,考慮到LED 的V-I 特性,目前大多數LED燈具均為電流控制模式[12-13]。 本文使用雙閉環控制系統,使驅動電路實現恒流輸出。 電路拓撲及控制策略分別如圖1 和圖2 所示[14]。
圖中,Ls、Rs為系統阻抗;R1為電流檢測電阻;C1為一次側支撐電容;C2為二次側支撐電容;VD5和VD6分別為導向二極管和續流二極管;is為網側電流;ik2為流過高頻變壓器支路的電流,MOSFET高頻開關狀態使得該支路產生高頻脈沖電流,此電流注入系統,是系統存在超高次諧波的根本原因。

圖1 電流控制模式LED 驅動電路拓撲Fig. 1 LED drive circuit topology in current-controlled state

圖2 雙閉環控制原理Fig. 2 Principle of double closed-loop control
雙閉環控制工作原理為:電路采用電壓電流控制策略,外環電壓控制通過對輸出電壓采樣得到采樣電壓Udc,與參考電壓Uref比較得到誤差放大信號Ur, 此時內環電流控制回路將流過R1的電流信號轉化為電壓信號UR1,與Ur進行比較,輸出信號Uf,通過PWM 電路得到開關管的控制信號。 由上述分析可得,通過改變R1的阻值,能夠限定輸出電流的閾值。 這使得內環控制的響應速度遠大于外環控制,因為一次側電流的變化瞬間便會引起UR1的變化。該控制策略在恒壓控制的基礎上加入了內環電流控制,使電路輸出電流穩定。
1.2 實測數據
本文結合LED 燈具實測數據, 對其超高次諧波發射特性進行分析,LED 燈具參數見表1。
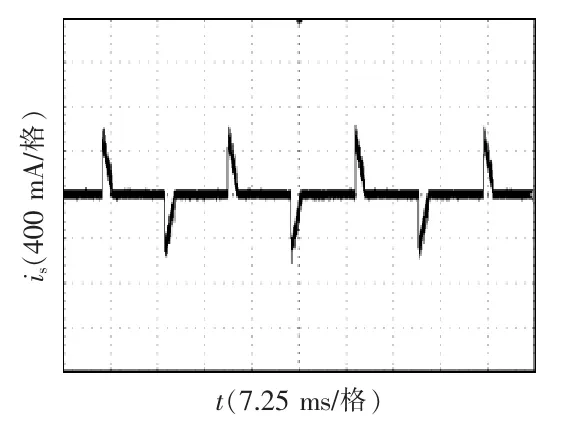
驅動電路采用HV9910B 型驅動芯片, 其工作頻率可通過外接定時電阻來自行設定, 設計IC 工作頻率為40 kHz 左右[15]。 使用電能質量測試分析儀IPQ-1 得到LED 燈具網側電流波形及超高次諧波波形,如圖3 所示。
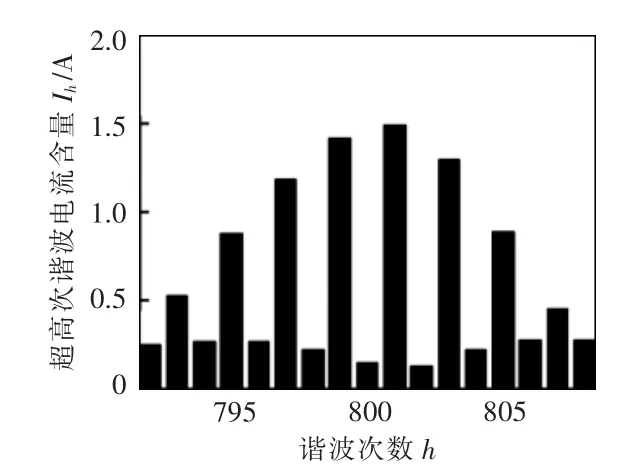
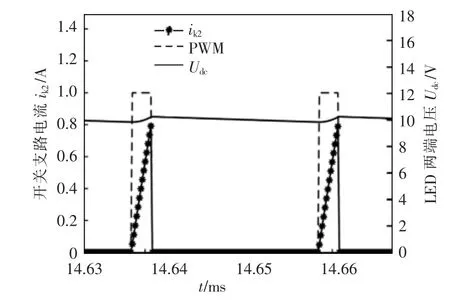
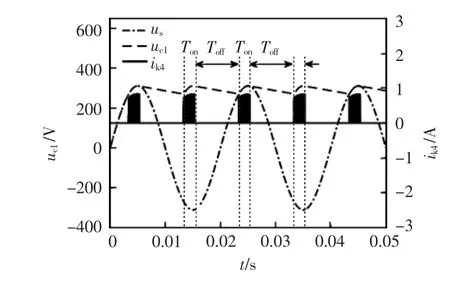
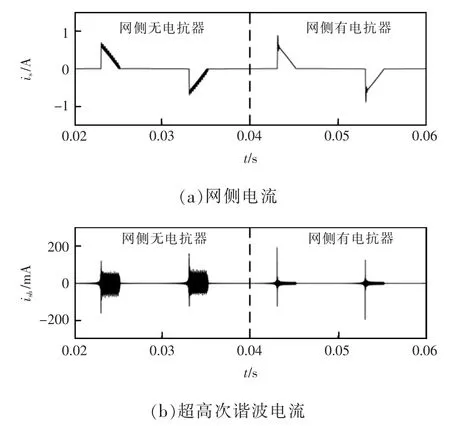
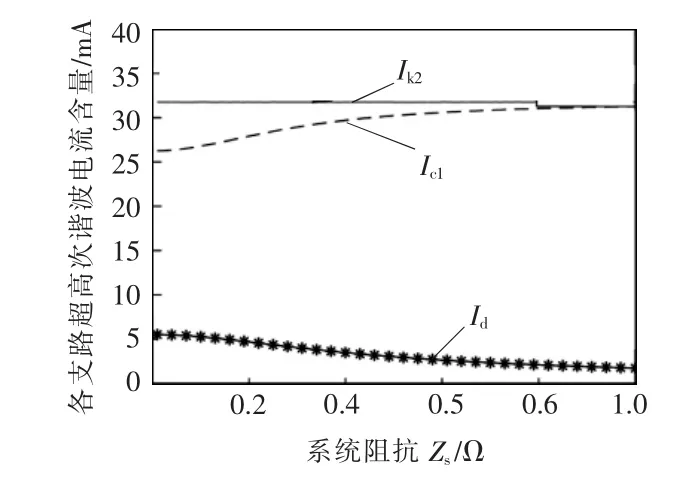
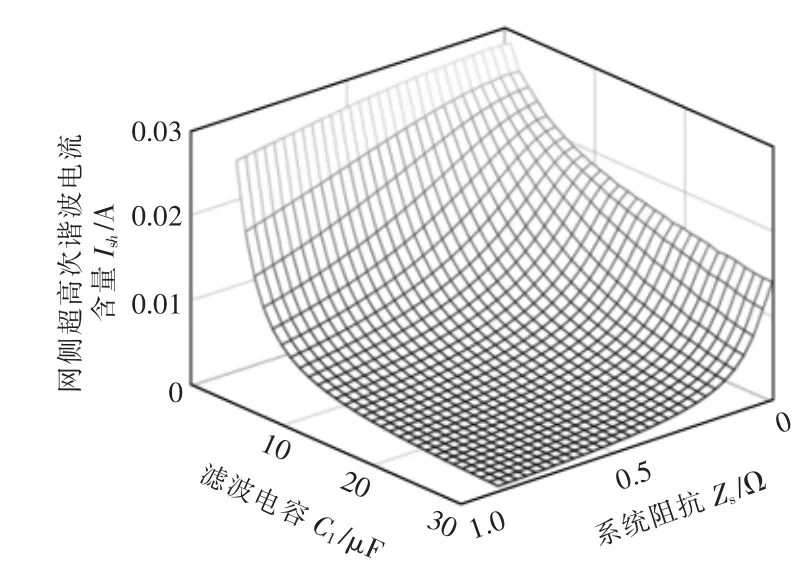
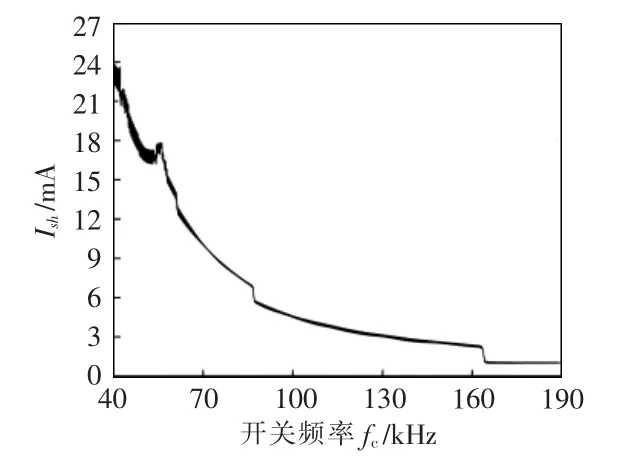
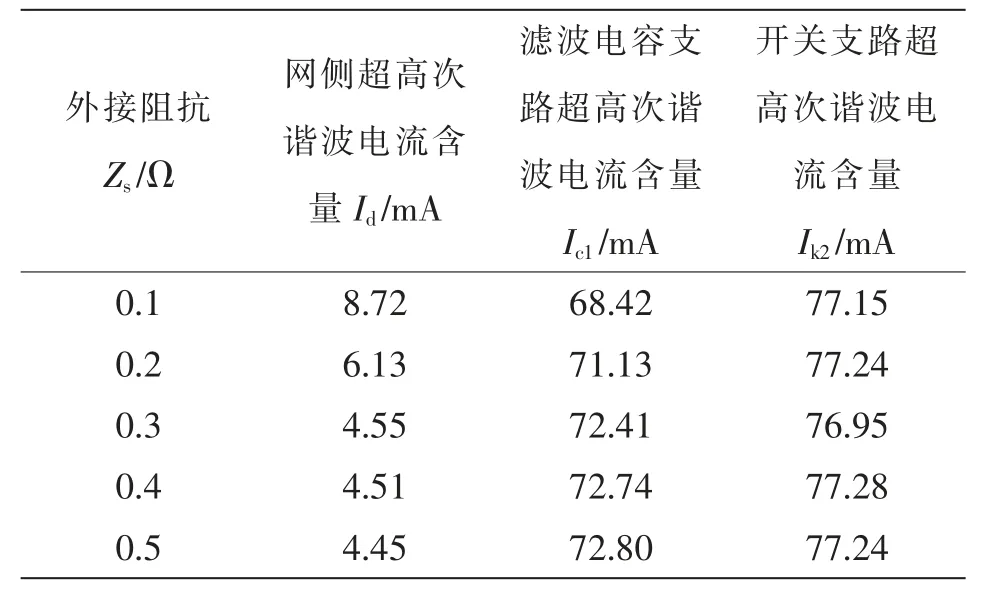
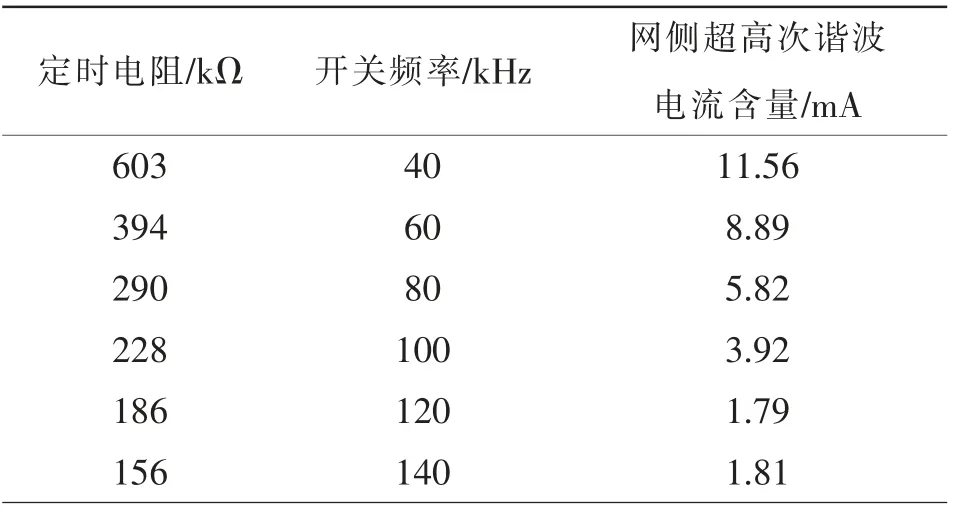
從LED 網側電流波形可以看出, 電流下降沿存在豐富的超高次諧波電流, 主要頻帶分布如圖4所示。 驅動芯片工作頻率在40 kHz 左右,所以開關支路超高次諧波電流頻帶主要分布在40 kHz 及其整數倍附近,而網側超高次諧波電流頻帶僅存在于40 kHz 左右, 因為80 kHz 及以上頻帶處濾波電容的阻抗ZC1與系統阻抗Zs存在以下關系:ZC1< 表1 A 品牌16 W LED 燈具參數Tab. 1 Parameters of 16 W LED lamp of Brand A 圖3 LED 燈具實測電流波形與超高次諧波波形Fig. 3 Measured current waveform and supraharmonics waveform of LED lamp 圖4 開關頻率處頻譜分布Fig. 4 Frequency spectrum distribution at switching frequency 二極管VD1和VD4在系統電壓過零點θ 角后導通,再經過導通角δ 后,整流橋被電容C1反向關斷, 其后由電容C1為后端電路供電。 導致電容C1兩端電壓下降的根本原因是后端電路有功消耗,在研究整流電路導通初相角θ 與導通角δ 時,按照功率等效的原則, 將該部分電路近似等效為電阻R3,R3=K2U2ref/P, 其中:K 為高頻變壓器變比;P 為LED功率。 整流電路導通初相角θ 與導通角δ 求解方程為 式中,ω 為系統工頻電壓角頻率。 在相關參數已知的前提下,采用牛頓迭代法即可求出對應的δ 和θ。 電網中超高次諧波產生原因已在上文做了簡要說明,現通過對MOSFET 導通時的LED 開關驅動電路建模研究, 來分析網側超高次諧波含量的影響因素。 圖5 為MOSFET 導通時的LED 等效驅動電路。 MOSFET 高頻開關狀態會產生高頻脈沖電流,該電流一部分流入濾波電容器C1,其余部分流入電網。 對0~T/2 內任意一個開關周期,MOSFET 導通時電路狀態方程為 式中:ik為0~T/2 內流過開關支路的電流;ΔU 為LED 兩端電壓波動范圍;t1為開關管閉合時刻;T 為電網工頻電壓周期;fc為開關頻率;N0∈{1,2,…};N∈{0,1,2,…};D1、D2、N1、N2、N3為常量。 圖5 MOSFET 導通時LED 等效驅動電路Fig. 5 LED equivalent drive circuit during MOSFET conduction MOSFET 任意開關時刻的求解,是構造開關函數的前提。 其中導通時刻t1由開關頻率fc決定,關斷時刻t2由LED 兩端電壓波動決定。 MOSFET 關斷瞬間電路狀態方程為 設t2時刻電容C1兩端電壓為Ut2,則有 開關支路會產生高頻脈沖電流ik2,但只有整流橋導通時該電流才會注入系統。 上文已對MOSFET任意開關時刻進行了求解。由此可以推導影響網側超高次諧波含量的開關函數表達式為 其中:Sk=1 時,表示整流橋VD1、VD4支路與MOSFET均導通;Sk=0 時,表示整流橋關斷或MOSFET 關斷;Sk=-1 時,表示整流橋VD2、VD3支路與MOSFET 均導通。 在整流橋導通時,|Sk|=1 等同于MOSFET 導通,控制信號與ik2和Udc的關系如圖6 所示。 圖6 控制信號與ik2 及Udc 關系Fig. 6 Relationship among control signal, ik2, and Udc 在t1時刻給MOSFET 觸發信號,開關支路有電流流過,LED 兩端電壓上升,t2時刻觸發信號消失,該支路電流降為0,LED 兩端電壓下降。 開關支路電流直接由流過LED 的電流決定,由于本文采用了恒流式控制策略,可將開關支路的電流等效為受控電流源ik2,可對此作出論證,等效電路如圖7 所示。圖中ik2= idc/K,令系統阻抗Zs=Rs+jnωLs,濾波電容C1容抗Zc1=-j/nωC。 則網側超高次諧波電流ik3的表達式為 則電流ik3的有效值可表示為 圖7 超高次諧波源模型Fig. 7 Supraharmonics source model 可以看出,LED 驅動電路網側超高次諧波電流主要由系統阻抗Zs、濾波電容Zc1、開關頻率fc、LED等值阻抗R2以及系統工頻電壓頻率ω 決定。 隨著系統阻抗Zs的增大, 由于分流作用超高次諧波電流會更多流入濾波電容C1, 使網側諧波含量降低,濾波電容C1的變化也會產生同樣效果;開關頻率fc的增大會使開關支路超高次諧波電流ik3的頻率升高,導致系統等效阻抗增大與濾波電容等效阻抗減小,從而對注入系統的超高次諧波電流含量產生影響;電網工頻電壓角頻率ω 通過改變整流電路導通角δ,對注入系統的諧波電流含量產生影響。 為驗證上述理論分析的正確性, 本文基于Matlab/Simulink 搭建LED 驅動電路仿真模型,電路采用雙閉環控制方式。整流橋導通時對應電壓電流關系如圖8 所示。圖8 中,us為系統電壓,uc1為支撐電容兩端電壓,ik4為整流橋導通時開關支路電流。考慮到超高次諧波的頻率特性,可通過在網側串聯小電抗器,來抑制網側超高次諧波電流ish。 裝設小電抗器前后網側電流及其中包含的超高次諧波電流波形如圖9 所示。 圖8 整流橋導通時對應電壓電流關系Fig. 8 Relationship between voltage and current during rectifier bridge conduction 圖9 網側電流及超高次諧波電流波形Fig. 9 Waveforms of grid-side current and supraharmonics current 由圖8 可以看出,Ton時段系統電壓絕對值|us|等于支撐電容兩端電壓uc1,整流橋導通,開關支路高頻脈沖電流ik4會在此段時間注入電網;Toff時段系統電壓絕對值|us|小于支撐電容兩端電壓uc1,整流橋關斷, 由支撐電容C1為后端電路供電,uc1下降。 開關支路由于MOSFET 高頻工作狀態,該支路形成了高頻脈沖電流,如圖10 所示。 流過LED 電流及其兩端電壓波形如圖11 所示。 圖10 開關支路電流波形Fig. 10 Current waveform in switching branch 圖11 LED 支路電壓、電流波形Fig. 11 Waveforms of voltage and current in LED branch 電路通過外環電壓控制使LED 兩端電壓波動不超過1%,同時通過內環電流控使流過LED 的電流波動不超過額定值的3%, 通過該控制方式可以起到較好的恒流穩壓作用。 上文論述了將超高次諧波源等效為受控電流源的原因,現通過仿真進一步驗證其正確性。 各支路超高次諧波電流含量如圖12 所示。圖12 中3 條曲線分別為濾波電容支路超高次諧波電流含量Ic1,注入系統超高次諧波電流含量Id以及開關支路超高次諧波電流含量Ik2。 由圖12 可以看出, 隨著系統阻抗Zs的增大,流入濾波電容C1的超高次諧波電流Ic1逐漸增加,注入系統的超高次諧波電流Id逐漸減少,且滿足基爾霍夫電流定律:Ik2=Ic1+Id。 而在Zs變化過程中,開關支路超高次諧波電流含量Ik2始終不變, 故將該支路看作受控電流源。 圖12 各支路超高次諧波電流含量Fig. 12 Supraharmonics current content in each branch LED 驅動電路網側超高次諧波電流含量受到多重參數影響,由式(9)可得其中主要影響因素有:系統阻抗Zs,濾波電容Zc1,開關頻率fc,LED 等值阻抗R2,以及系統工頻電壓頻率ω 等。 由于工頻電壓頻率ω 變化不大,故忽略其對Ik3的影響。系統阻抗Zs及濾波電容C1對網側超高次諧波的影響如圖13所示。 圖13 系統阻抗與濾波電容對網側超高次諧波電流含量影響Fig. 13 Influences of system impedance and filter capacitor on grid-side supraharmonics current content 電容C1與系統阻抗Zs的增大均會減小網側超高次諧波電流含量,且在電容C1較小時,系統阻抗對網側超高次諧波含量影響并不明顯, 符合式(9)所描述的超高次諧波特征。 圖13 也為超高次諧波的治理提供了一些思路,如:在做驅動電路設計時,應綜合考慮元件參數對超高次諧波發生量的影響;利用超高次諧波的頻率特性,通過在網側串聯小電感,便可很好地抑制網側超高次諧波電流含量。 網側超高次諧波電流主要來自于開關支路,由于該支路上MOSFET 高頻開關狀態,造成了高頻脈沖電流。網側超高次諧波電流含量與開關頻率的關系如圖14 所示。隨著開關頻率fc的增大,網側超高次諧波含量逐漸降低,因為fc增大會導致開關支路電流頻率升高,進而影響濾波電容支路與網側的等效阻抗,使超高次諧波更多注入濾波電容C1。 注入電網的超高次諧波由兩部分組成:ik2分流到電網中的超高次諧波;整流電路產生的微量2~5 kHz 超高次諧波。 其中第二部分無法被直流側濾波電容C1濾除,使得fc增大到一定值后網側超高次諧波含量基本不變。 圖14 開關頻率對網側超高次諧波電流影響Fig. 14 Influences of switching frequency on grid-side supraharmonics current 對LED 燈具進行測試分析,其參數見表2。 表2 A 品牌10 W LED 燈具參數Tab. 2 Parameters of 10 W LED lamp of Brand A 驅動電路采用HV9910B 型驅動芯片, 使用220 V/50 Hz 標準源為驅動電路供電,圖15 和圖16分別給出了網側不加電抗器與加電抗器時LED 電流波形,其中電抗器L=1 mH。 由圖15 可見,LED 并網側無電抗器LED 電流波形的下降沿存在豐富的超高次諧波電流。由于系統阻抗較小,當諧波源功率較大時將會有大量超高次諧波注入系統。利用上文所提的恒流式諧波源模型,可以通過增加網側阻抗,來抑制超高次諧波注入系統。 圖15 并網側無電抗器LED 電流波形Fig. 15 Current waveform of reactor-free LED on grid-connected side 圖16 并網側加電抗器LED 電流波形Fig. 16 Current waveform of LED with reactor on grid-connected side 在LED 并網側加電抗器后,LED 電流下降沿超高次諧波受到了明顯抑制。進一步驗證了上文分析的正確性。 為減小測量誤差使用驅動電路同時對7 個同功率LED 供電。 在網側接入0.1、0.2、0.3、0.4、0.5 Ω電阻模擬系統阻抗,可以得到網側超高次諧波電流含量、濾波電容支路超高次諧波電流含量以及開關支路超高次諧波電流含量,如表3 所示。 由表3 可見,隨著外接阻抗變化,開關支路超高次諧波電流含量基本不變,該結論驗證了上文所提受控電流源模型的合理性。通過改變驅動芯片外接定時電阻阻值來設定驅動電路的開關頻率,不同開關頻率下網側超高次諧波電流含量見表4。 由表4 可見,隨著電路開關頻率的升高,網側超高次諧波電流含量呈現下降趨勢。該結論對上文仿真所得趨勢進行了驗證。 表3 系統阻抗對超高次諧波含量影響Tab. 3 Influences of system impedance on supraharmonics content 表4 開關頻率對網側超高次諧波含量影響Tab. 4 Influences of switching frequency on grid-side supraharmonics content 本文通過對電流控制模式LED 驅動電路實測數據分析及相關建模研究,推導出網側超高次諧波電流開關函數Sk,以及多重參數影響下網側超高次諧波電流含量Ik3表達式。 研究發現,系統阻抗的變化不會對開關支路超高次諧波含量造成影響,并在此基礎上提出了超高次諧波電流源等效模型。開關頻率fc通過改變超高次諧波電流源頻率,進而影響Zs與Zc1以及網側超高次諧波電流含量。 考慮到超高次諧波的頻率特性, 通過在網側串聯小電抗器,可對注入電網的超高次諧波電流起到較強的抑制作用。本文研究內容對開關驅動電路超高次諧波分析及并網超高次諧波源的治理具有參考意義。

2 超高次諧波產生機理
2.1 整流電路導通初相角與導通角的求解

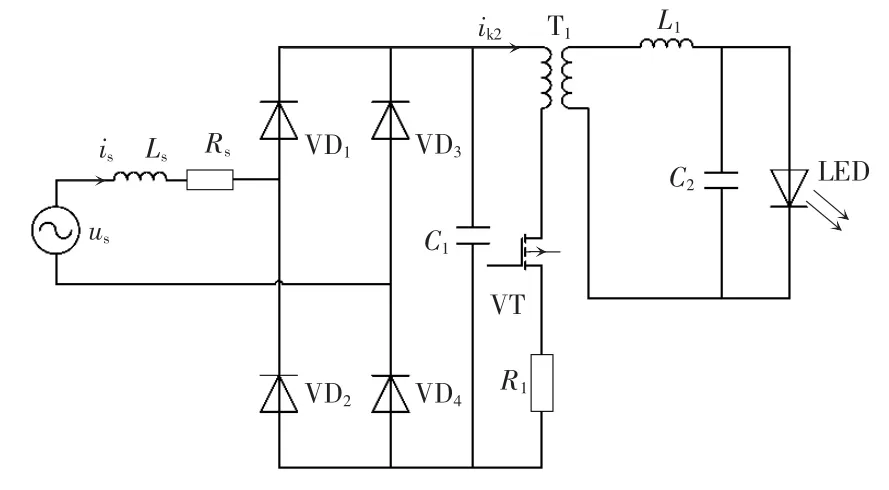
2.2 開關支路電流及開關時刻的求解
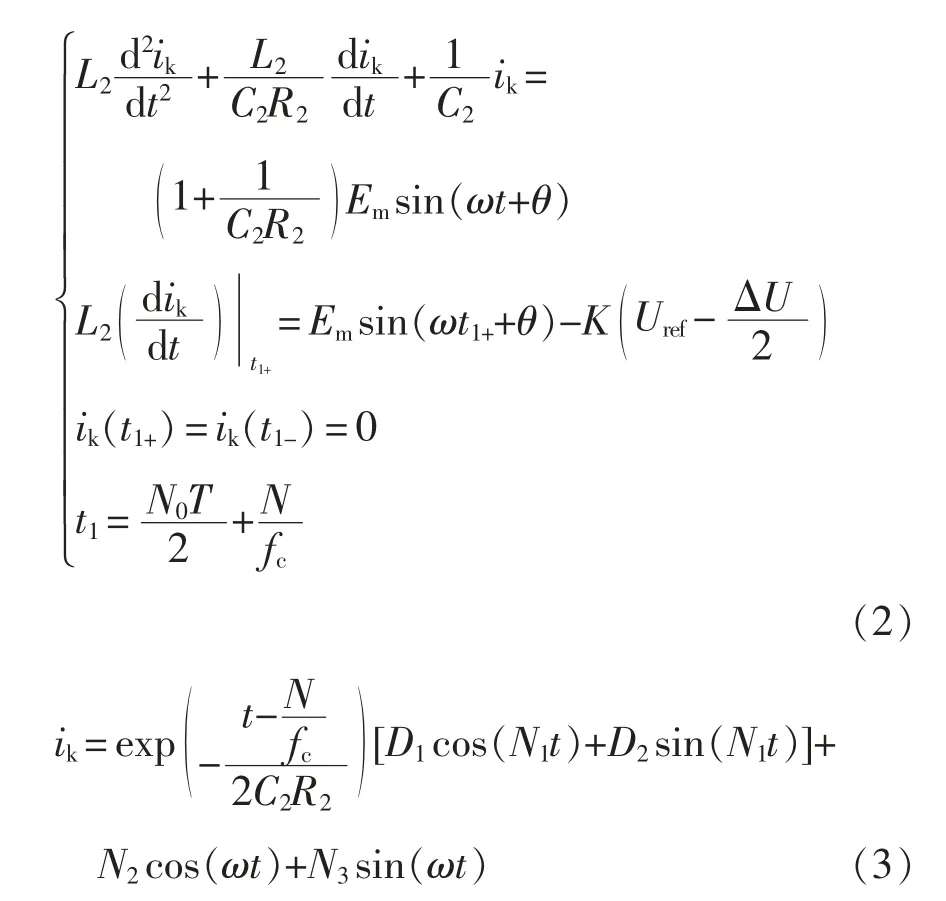

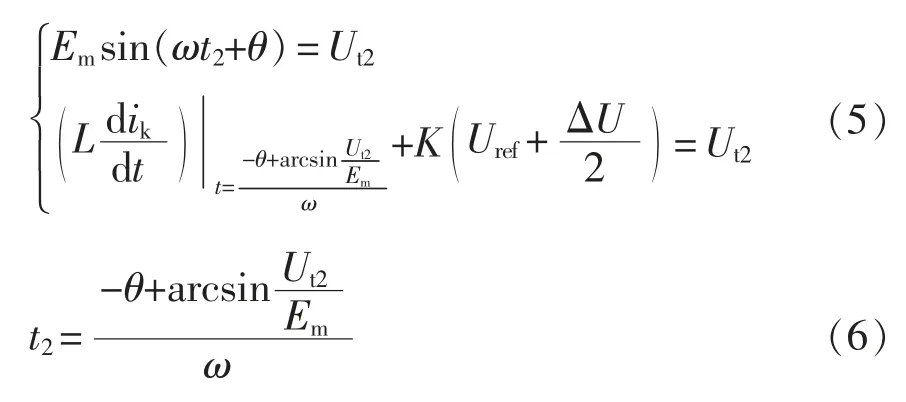
2.3 驅動電路開關函數的構造及網側超高次諧波計算
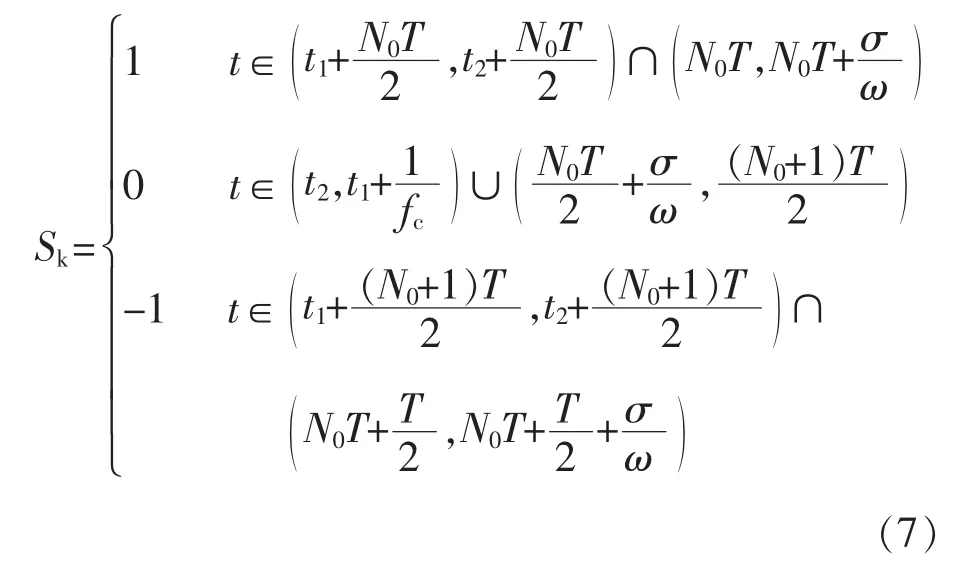

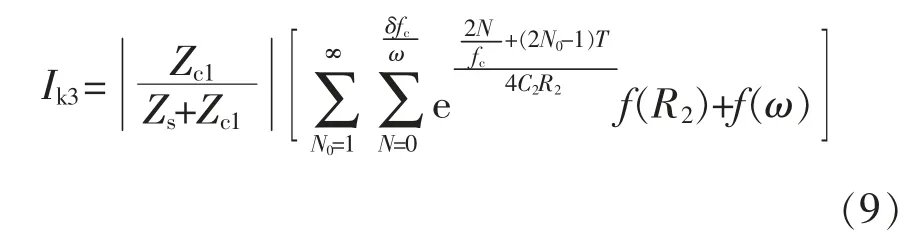
3 超高次諧波發射特性仿真驗證
3.1 仿真數據分析


3.2 超高次諧波源驗證
3.3 各參數對網側超高次諧波電流含量的影響
4 實測數據分析


5 結語

