從簡單模型入手探究陀螺儀在磁場中的減速問題

馮 鑫，范弘杰，程玉錕，趙 偉，陶小平，浦其榮，趙 霞，張增明

(中國科學技術大學 物理學院，安徽 合肥 230026)

近年來基于IYPT(International Young Physicists’ Tournament)題目的中國大學生物理學術競賽活動在國內高校中開展的越來越廣泛.這些具有很強開放性和可探索性的題目每年吸引了很多同學投入到相關學習和研究工作中，激發了同學們學習物理知識的熱情，通過開展相關的教學和比賽活動有效提升了高校普通物理的教學質量.

2019年的IYPT題目中的第12題是一道關于磁致減速的問題. 一個由非鐵磁性的導電材料制成的旋轉的陀螺儀，被置于磁場中時會減速，要求研究相關參數對于減速的影響.

對于這個磁場中導體材料陀螺的減速問題可以用電磁學知識來初步定性分析，導電材料在磁場中運動時切割磁感線會產生動生電動勢，產生的感應電流在磁場中會受到安培力，安培力矩作為阻礙陀螺儀旋轉的阻力矩會導致陀螺減速.

一般磁場下陀螺儀的減速問題可以用麥克斯韋方程組求解，但過程較為復雜，也難以設計實驗方案進行可重復性的定量驗證. 本文以磁場中的無限長導體圓柱模型為基礎，分析了陀螺儀轉軸與磁場方向間不同角度下磁場導致陀螺儀減速的機理，得到了該模型下電磁阻力矩的近似表達式，并進行了量綱分析. 實驗上為了能相對直接評估電磁阻力矩的大小，將力學量測量轉換為電動機驅動電流測量，以直流永磁電動機驅動陀螺儀，驗證了所建立模型的理論分析結果，歸納出陀螺儀減速過程中電磁阻力矩所滿足的一般關系.

1 理論分析

減速問題中的磁場分布，在理論和實驗中都只考慮均勻磁場情況，并不影響分析該問題的主要物理圖像. 對于非均勻磁場,需要在分析中加入磁場梯度的影響[1]，或者簡單的選擇一個特定位置的磁感應強度值[2]，作為整個磁場代表值. 對于這個問題中磁場方向和陀螺儀轉軸方向的相對取向，先考慮磁場方向垂直于轉軸和平行于轉軸兩個特殊方向，再擴展考慮一般情況. 磁場方向垂直于轉軸，即平行于轉盤時，如圖1所示，為分析方便選擇區域為包含全部陀螺儀的勻強磁場；磁場方向平行于陀螺儀轉軸時，若勻強磁場范圍很大，包含整個陀螺儀，則顯然旋轉陀螺儀轉盤中不會產生渦流[2]，也就不會產生電磁致減速現象，這一點在實驗上也可以明顯觀察到. 因此分析磁場方向平行于陀螺儀轉軸時，假定陀螺儀圓盤上的一個小區域內施加軸向磁場.

1.1 磁場方向與陀螺轉軸方向垂直

嚴格建模計算陀螺儀轉子產生渦流的電磁阻力矩，需要根據麥克斯韋方程組，結合邊界條件進行求解，過程相對復雜[2,3]，考慮到陀螺儀可認為是繞定軸轉動的圓盤，可以利用簡單的導體圓柱模型分析電磁阻力矩的產生過程.

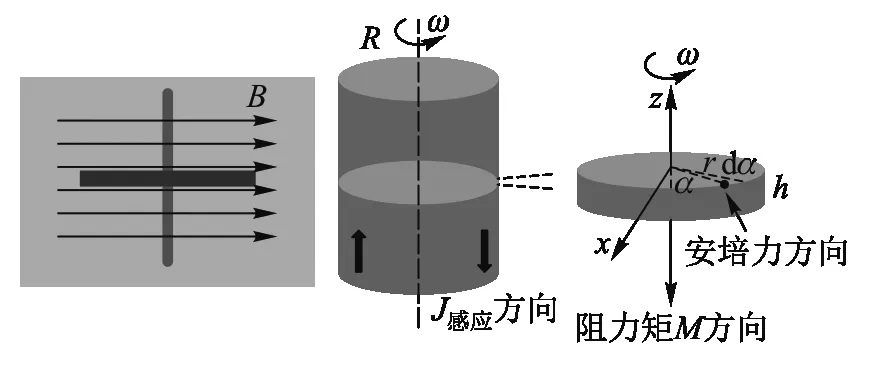
圖1 磁場方向垂直轉軸位形和無限長導體圓柱模型

如圖1所示，若有一個無限長繞軸以角速度ω旋轉的圓柱形導體，其半徑為R，電導率為σ，密度為ρ，置于方向垂直于轉軸的無限大勻強磁場中,磁感應強度為B. 該圓柱導體可看成距自身轉軸距離不同的很多導體微元組成，如圖1所示，這些導體微元切割磁感線會產生感應電流J感應. 截取該圓柱體上高度為Δh的一段圓盤進行分析，在忽略渦流產生的磁場的情況下，取與x軸夾角為α，角度為d的扇形區域，該扇形區域上距圓心r處的微元dr，其截面積為ds=rddr，如圖1所示. 磁場方向水平指向右側時，該微元所受安培力垂直紙面向外，即產生垂直向下的阻力矩,阻礙陀螺轉動. 此時高度為h的微元產生的總動生電動勢e可表示為

e=BΔhωrsinα

(1)

由微觀歐姆定律，有

σG=j

(2)

其中G為單位長度導體切割磁感線產生感應電動勢，j是電流密度. 上兩式中e和G又顯然滿足：

e=ΔhG

(3)

聯立上述式(1)-(3)可以得到

j=σBωrsinα

(4)

進而可以得出該導體棒在磁場中受到的安培力矩的表達式[6]為

dM=σωΔhB2r3(sinα)2drdα

(5)

對式(5)進行積分可以得到單位高度的導體圓柱的安培力矩表達式為

(6)

從式(6)可以看出，安培阻力矩與磁感應強度的二次方和角速度的一次方成正比. 同時考慮到雖然陀螺儀一般為厚度有限的圓盤，但由于圓盤與無限長圓柱具有相同的軸對稱性，且產生減速效應的電流只是軸向電流，因而該問題中的陀螺儀圓盤受到的安培阻力矩與該理想模型應只相差一個和盤厚、半徑有關的系數，若陀螺儀圓盤厚度為h，半徑為R，則根據式(6)其所受的安培力矩可表示為

M垂直=λ(h,R)σhB2R4ω

(7)

對于磁場中的陀螺儀減速過程，除電磁阻力矩外，還應考慮空氣阻力和摩擦等阻力的作用. 整體減速效應可以近似取到常值阻尼和與速度成一次關系的一次阻尼，忽略高次項，即

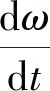
(8)

其中k為阻尼系數，對式(8)求解可得到角速度的減速過程公式為

(9)

式(9)說明，陀螺儀的角速度隨時間滿足指數衰減關系. 此外可以注意式(9)中的阻尼系數應包含非磁場產生的k0和磁場產生kB兩部分，即

k=k0+kB

(10)

根據剛體轉動定律，總阻力矩M，剛體轉動慣量I，以及角加速度應滿足如下關系:

(11)

式(11)中M其他為其他因素產生的阻力矩，圓盤的轉動慣量I為

(12)

其中ρ為導體圓盤的密度，結合式(8)、(10)、(11)可得

M垂直=IkBω

(13)

將式(7)和(12)帶入式(13)，磁場的安培阻力矩產生的阻力系數為

(14)

1.2 磁場方向與陀螺轉軸方向平行

當磁場方向平行于陀螺圓盤轉軸時，如前所述可假定磁場只作用于轉盤上一個小的矩形區域[3]，如圖2所示，該區域置于距圓盤中心充分遠的位置，磁場垂直盤面. 穩定后在某一固定時刻，由于導體切割磁感線產生動生電動勢，相當于在導體圓盤上“嵌入”一個“電池”，而流經該區域的電流將受安培力作用，這時圓盤受到一個阻礙其運動的安培力矩，因而減速. 對一般情況，可以將不規則、不均勻的磁場分割為多個小的這類均勻磁場，這時關于圓盤軸無旋轉對稱性的磁場也一定具有減速效應.

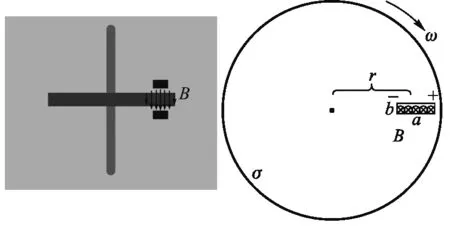
圖2 磁場方向平行轉軸位形和圓盤上矩形均勻磁場小區域模型

若磁場區域沿電流方向長為a,垂直電流方向寬為b，此區域距離盤心為r,圓盤電導率為σ,陀螺圓盤厚度為h. 某一時刻，圓盤的旋轉角速度大小為ω，則該均勻磁場區域導體切割磁感線產生的動生電動勢e為

e=Baωr

(15)

若此區域相對圓盤充分小，此時等效電池的內阻可以表示為

(16)

為得到感應電流需要計算外電阻，等效外電阻的求解需要算出整個盤面的電流分布，但若磁場位形確定時，等效外電阻阻值一定為一常量，記為R,則由歐姆定律得

I=ασBbhωr

(17)

式(17)中α是磁場位形和圓盤幾何尺寸確定時的常數，其滿足

(18)

于是此時安培力矩可以表示為

M平行=ασB2abhωr2

(19)

從式(19)可以看出，與磁場方向垂直轉軸時的結果類似，此時安培阻力矩也與磁感應強度的二次方和角速度的一次方成正比.

1.3 直流電機轉矩與阻力矩

為更方便的研究電磁阻力矩與磁場及角速度的相互依賴關系，實驗中引入額定電壓為6V的130式直流永磁電機輔助，利用其一定電流下的轉矩來平衡電磁阻力矩，進而將力學量測量轉換為電動機驅動電流測量. 一定轉速范圍內，直流電動機穩定時的輸出轉矩與其電樞電流強度平均值有非常好的線性關系[4,5]，即

M=η(I-I0)

(20)

當直流電機驅動陀螺儀以穩定角速度轉動時，應滿足

MB+Mf=M

(21)

其中MB為電磁阻力矩，Mf為摩擦力阻力矩，結合式(10)可知Mf應滿足

Mf=k0ω

(22)

由式(7)和式(20)—(22)可得，磁場方向垂直于陀螺儀轉軸時，電機驅動電流和磁感應強度和角速度的依賴關系為

(23)

由式(19)-(22)可得，磁場方向平行于陀螺儀轉軸時，電機驅動電流和磁感應強度和角速度的依賴關系為

(24)

1.4 量綱分析

在式(7)、(19)或式(23)、(24)中可以發現，電磁阻力矩與磁感應強度平方成正比，和角速度成正比. 對于這一點，從物理分析中的量綱分析方面也可以進行說明.

對于旋轉陀螺儀在磁場中受到的磁力矩M,可能與外磁場磁感應強度B，旋轉角速度ω，材料電導率σ，以及系統幾何參量(不妨統一記為D)有關. 若假定長度、質量、時間、電流的量綱分別為L、M、T、I，則各物理量的量綱表示如下:

[B]=L0M1T-2I-1

(25)

[ω]=L0M0T-1I0

(26)

[σ]=L-3M-1T3I2

(27)

[D]=L1M0T0I0

(28)

若電磁力矩滿足

M=λBαωβσγDδ

(29)

式(29)中λ為無量綱常數. 同時力矩M的量綱滿足

[M]=L2M1T-2I0

(30)

即可解得

M=λB2ω1σ1D5

(31)

量綱分析的結果式(31)與式(7)、式(19)的結果一致，關于電磁阻力矩的推導結果可以認為是合理的.

1.5 磁場方向相對于陀螺儀轉軸取向任意角度時

當磁場方向相對于陀螺儀轉軸方向取向任意時，情況較為復雜，但可以在之前兩種特殊情況基礎上，對任意取向下的減速過程作粗略的討論. 此時可令磁場方向始終為水平方向，陀螺儀轉軸與豎直方向夾角為α.

磁場方向平行于陀螺儀轉軸的部分可認為沒有減速效應，故公式中只應包含垂直于轉軸的減速效應，即cosα項. 同時陀螺儀自身與摩擦有關的一次阻尼系數也將發生變化，阻尼系數與作用力大小成正比，故公式應包含sinα和cosα項. 由于垂直于轉軸的磁場分量激發的沿盤面的渦流會受平行于轉軸(垂直于盤面)的磁場分量產生的安培阻力矩，即兩方向磁場的減速效應不獨立存在，故公式應包含sinαcosα交叉項[7,8].

基于上述考慮，磁場方向相對于陀螺儀轉軸取向任意時減速系數k應滿足如下關系

k=acosα+bsinα+ccos αsinα+d

(32)

式(32)中a、b、c、d為待定的角度無關參數.

2 實驗驗證

2.1 磁場方向與陀螺轉軸方向垂直時的減速過程實驗

在理論分析1.1中的式(9)表明陀螺儀的角速度隨時間滿足指數衰減關系，這種依賴關系可以在實驗中進行實際檢驗.

圖3 黃銅陀螺儀、亥姆霍茲線圈和高斯計

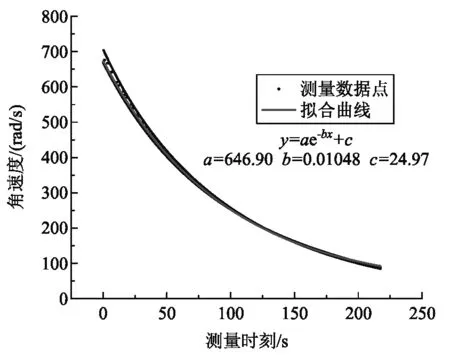
圖4 陀螺儀角速度和時間關系曲線

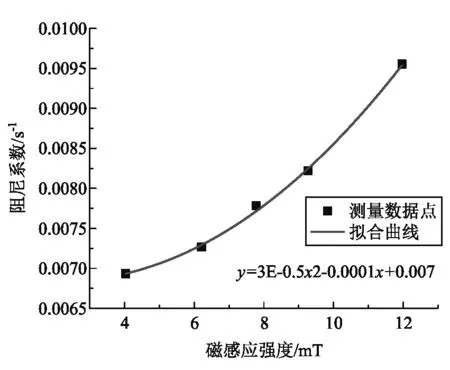
圖5 阻尼系數k與磁感應強度關系曲線

實驗中使用了如圖3中所示黃銅制陀螺儀.先將陀螺儀加速到一定轉速，之后迅速將其固定于亥姆霍茲線圈產生的勻強磁場之中，磁場方向垂直于陀螺儀轉軸. 實驗中使用光電門搭配擋光片測量計算旋轉陀螺儀的速度，使用圖3中的高斯計測量磁感應強度. 根據測量數據描繪磁場下的角速度(可轉換為線速度)隨時間依賴關系，并扣除無磁場時的影響.

實驗中測量了多個磁感應強度下陀螺儀的減速過程，可將這些減速過程與式(9)進行比較分析. 圖4是磁感應強度B=12 mT時的減速曲線，其中擬合曲線使用式(9)類型函數y=ae-bx+c進行擬合，可以看到擬合曲線和測量數據點匹配較好，陀螺儀在磁場中的減速過程可認為符合指數衰減規律. 也可將不同磁場下的減速過程數據(擬合曲線)對時間求導，研究減速過程的阻尼系數k與磁場應強度的依賴關系，從前面理論分析部分式(8)-(11)可以看出，阻尼系數與磁感應強度間應符合二次函數拋物線型依賴關系. 圖5是由測量數據計算得到的阻尼系數與磁感應強度關系曲線，其變化趨勢與式(14)相似的二次函數擬合曲線符合的較好.實驗上佐證了前述理論部分的合理性.

2.2 直流電動機驅動實驗

圖6 勻強磁場中的直流電動機驅動實驗儀器

通過引入直流電動機作為驅動，利用式(20)—(24)可以更直接地測量和分析特定角速度和磁感應強度下的電磁阻力矩. 實驗中使用如圖6中所示的130式永磁有刷直流電機，將其與陀螺儀鏈接后，放入勻強磁場中. 用“上行下行法”調節電流大小并記錄與之對應的穩定角速度值.

固定磁場磁感應強度不變時，根據式(23)，表征力矩大小的驅動電流應與陀螺儀穩定轉動的角速度成線性關系，同時與外磁場磁感應強度成二次函數關系. 實驗中改變磁場時難以保證陀螺儀轉速穩定不變，因此只在固定外磁場條件下測量了轉速穩定時陀螺儀旋轉角速度和驅動電流的依賴關系. 實驗中固定不同外磁場強度下進行了多組測量，驅動電流與陀螺儀穩定轉動的角速度之間顯示了很好的線性關系，圖7中下圖是磁感應強度為193.82 mT的測量數據，可以看到線性關系符合的較好.

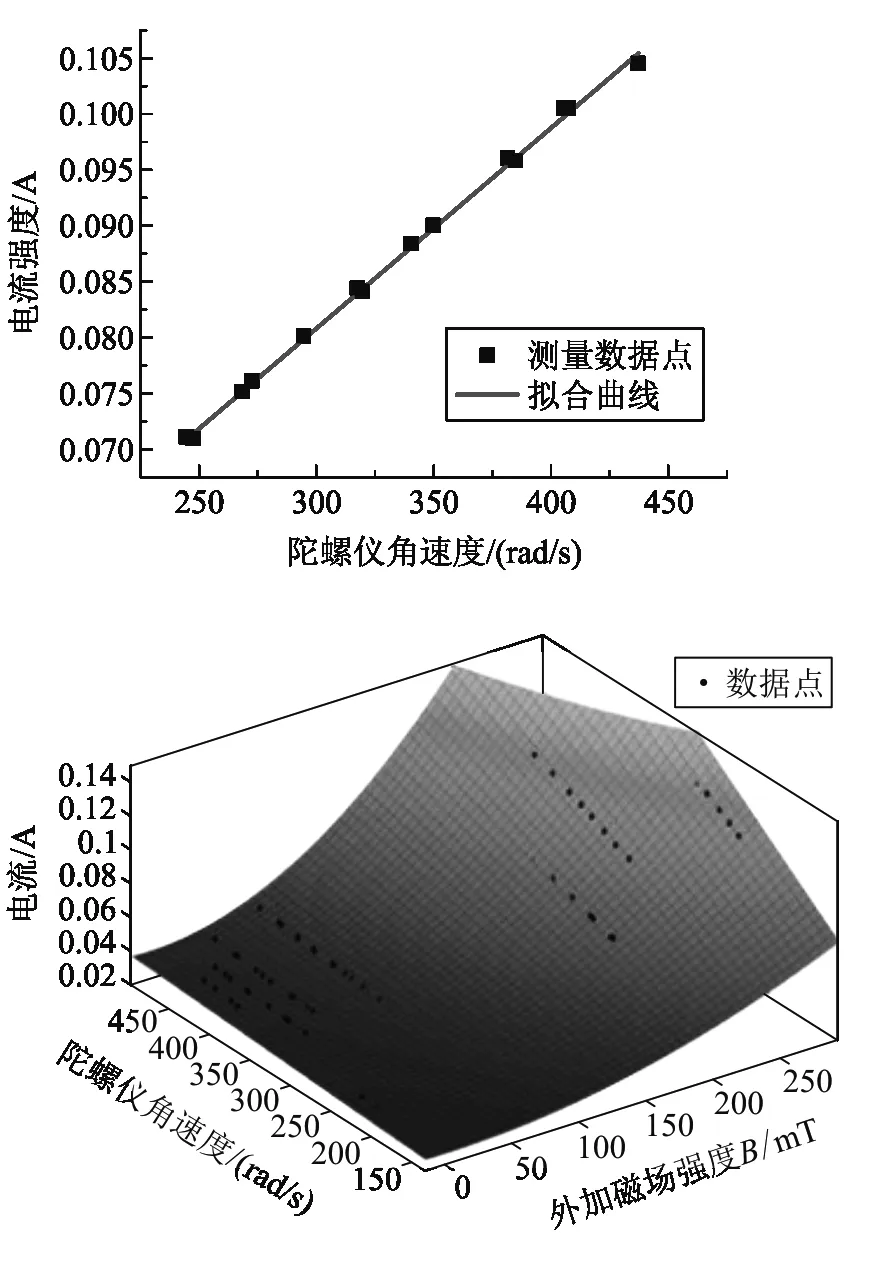
圖7 直流電動機電樞電流與外加磁場和陀螺儀轉速關系

將測得的電動機電樞電流、陀螺儀轉速和磁感應強度在一個三維坐標中作圖，數據關系用式(23)來進行擬合，從圖7中右圖來看，擬合曲線與實驗數據點符合較好. 說明前述模型和假設條件基本合理，可用來解釋陀螺儀在磁場中的減速過程.

2.3 磁場方向平行于陀螺儀轉軸時的減速實驗

當磁場方向與陀螺儀轉軸平行時，根據前述理論分析，磁場范圍限制在圓盤上的一個小區域中. 如圖8所示，實驗中將一個相對大且薄的鋁盤作為陀螺儀圓盤，圓盤材質為6061鋁，直徑159.40 mm，厚度2.60 mm，直流電機提供驅動力，固定兩塊相同磁鐵于圓盤上下兩側正對相吸，使磁感線垂直穿過圓盤上一個相對小的區域，磁鐵尺寸為10 mm×10 mm×25 mm. 通過改變磁鐵個數和間距以改變磁感應強度，通過改變磁場夾持裝置位置以改變磁場到圓盤中心的位置. 使用光電門和擋光片測量不同磁感應強度下，圓盤穩定旋轉時的角速度.

圖8 磁場方向平行于陀螺儀轉軸整體裝置和光電門

實驗中使用如圖8中右圖所示光電門測量穩態旋轉狀態的角速度平均值，利用穩定狀態的電動機電樞電流和磁感應強度測量值可驗證其相互依賴關系. 從測量數據可以看出，磁場大小和位置固定時陀螺儀圓盤穩態角速度和電動機電樞電流，即電磁阻力矩的依賴關系，和式(19)一致，符合線性關系，圖9所示為磁感應強度B=100 mT時圓盤角速度和電動機電樞電流關系擬合結果，可認為符合線性關系.

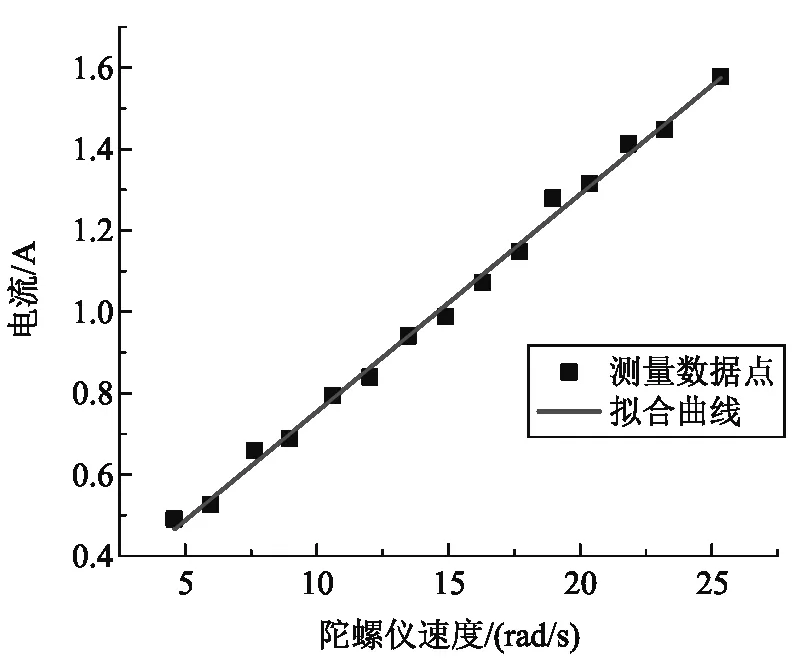
圖9 磁場方向平行陀螺儀轉軸且B=100 mT時角速度和電動機電流的關系

實驗中通過改變盤片上下兩側永磁鐵個數(保持最近兩個永磁鐵位置不變)，改變圓盤上固定區域的磁感應強度，在不同磁感應強度下得到與圖9類似的不同線性依賴關系的斜率. 圖10是不同線性斜率與磁感應強度B的依賴關系，擬合曲線顯示明顯的二次函數特性，與式(23)和(24)的結果符合較好. 實驗中高斯計存在零點漂移導致二次函數最低點有一定偏移.

圖10 磁場方向平行于陀螺儀轉軸時，阻尼系數與磁感應強度的依賴關系

1.2中的式(16)是以磁場區域相對陀螺圓盤無限小為基礎的，根據式(19)，若認為r的改變對系數α影響很小，使α幾乎不變，那么有電磁阻力矩應與磁場區域距離圓盤中心距離r的二次方成正比的結論. 實驗中通過改變磁場區域距離圓盤中心的距離r，得到了阻尼系數相對于r的關系，如圖11所示，實驗測量結果并不是明顯的二次函數關系，在距離圓盤中心較近時近似線性關系，r>5 cm(圓盤半徑大約7.5 cm)但仍在圓盤范圍內時阻尼系數隨r變化非常緩慢，趨近于飽和. 推測α應該依賴于r，在r較小時可以認為二者成反比關系，這一實驗結果有待于嚴格的理論分析.

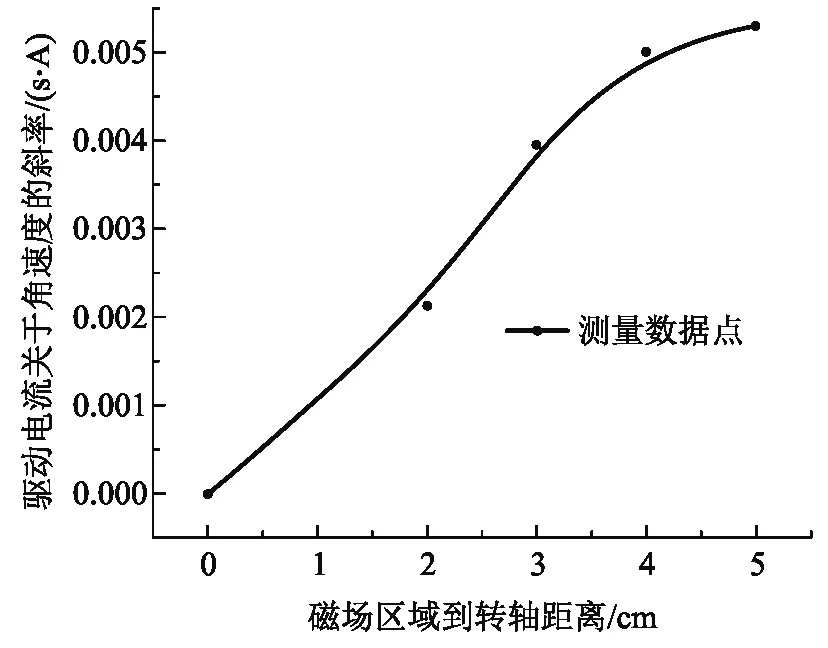
圖11 電流和角速度的關系系數與磁場區域到圓盤中心距離r的關系

2.4 磁場方向相對陀螺儀轉軸任意取向時的減速過程

圖12 改變陀螺儀轉軸與磁場方向夾角的減速實驗裝置

為了對1.5中得到的磁場方向相對于陀螺儀轉軸任意取向時的減速過程滿足的關系式(32)進行實驗驗證，實驗中將陀螺儀加速后，以不同取向放入水平勻強磁場，使陀螺儀轉軸與豎直方向夾角α. 如圖12所示，通過自制的角度測量板可以近似測量夾角α，在不同角度下，通過光電門并配合擋光片測量陀螺儀的減速過程.

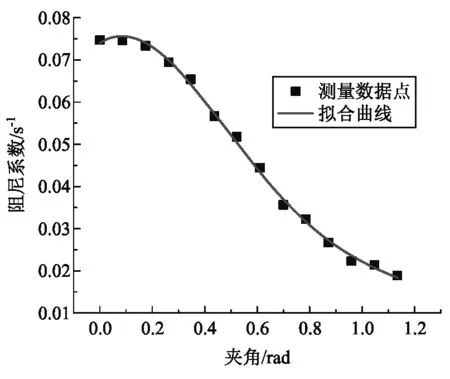
圖13 陀螺儀轉軸與豎直方向夾角α與阻尼系數關系

實驗中保持磁感應強度在51.4 mT, 陀螺儀與豎直方向夾角α從0°到65°，每隔5°測量一次陀螺儀的減速過程，將測量計算得到的阻尼系數與陀螺儀轉軸與豎直方向夾角α的關系用式(32)進行擬合，擬合結果如圖13所示，可見阻尼系數與夾角α的依賴關系與式(32)符合的較好. 結合分析過程可以進一步推測若陀螺儀自身阻尼較小可忽略時，式(32)中的cosα項應可忽略[7,8].

2.5 陀螺儀減速過程與材料電阻率的關系

陀螺儀減速問題中，所用陀螺儀導體材料的電阻率涉及能量的耗散，電阻率變化時應會影響減速過程. 從前述理論分析式(23)和(24)可以看出，陀螺儀減速過程中的電磁阻力矩與電阻率成正比. 為驗證這一推論，實驗上需要保證在其他參數相同的狀態下改變陀螺儀材料種類，這一實驗還需要進一步的詳細研究.

3 總結

IYPT題目普遍具有較強開放性和可研究性. 非鐵磁性導體的陀螺儀在磁場中減速這個問題中，陀螺儀所用導體材料、陀螺儀尺寸、結構和磁場相關參數都是開放的，題中可變條件非常多，不易通過麥克斯韋方程組給出全面且統一的答案.

本文從無限長導體圓柱模型入手，通過合理的近似推導得到了陀螺儀轉軸與磁場方向垂直和平行兩種條件下電磁阻力矩與磁感應強度、角速度、電導率等參數的依賴關系的表達式，進一步分析得到了磁場方向相對陀螺儀轉軸任意取向時陀螺儀減速阻尼系數的表達式. 為驗證理論分析的合理性，首先使用量綱分析進行了初步驗證，之后在實際實驗中引入直流電動機提供驅動轉矩，通過測量和數據分析比對，驗證了基本模型推導得到的電磁阻力矩和減速過程的合理性. 通過理論和實驗的分析可以得出，在陀螺儀轉軸與磁場方向垂直和平行時，電磁阻力矩與磁感應強度的二次方和角速度的一次方成正比. 當磁場方向相對陀螺儀轉軸任意取向時,阻尼系數滿足式(32). 陀螺儀在磁場中受到的電磁阻力矩與陀螺儀電阻率成正比.