驅動馬達定向運動的隨機動力學模型
楊紫貝,邱 星,陳巧妮,王海燕
(北京師范大學 物理學系,北京 100875)
分子馬達既具有酶的活性又具有運動活性,能夠將三磷酸腺苷(ATP)水解產生的化學能轉化為機械能,負擔著包括肌肉收縮、細胞活動和細胞內物質輸運等幾乎所有的生物活性運動[1].為理解分子馬達定向運動的物理機制,國內外學者從理論和實驗方面開展深入研究[2-6],其中基于費恩曼棘輪思想的“布朗馬達”是重要的理論模型之一[7].布朗馬達是將分子馬達抽象為處于非對稱周期勢中的布朗粒子,在熱噪聲和非平衡漲落的條件下,能產生定向運動的物理模型.其中,非對稱周期勢表示分子馬達與軌道的相互作用,這一作用導致布朗馬達系統的對稱性破缺;熱噪聲反映環境對分子馬達的影響,引起布朗粒子的擴散運動;非平衡漲落是由ATP水解產生的,為驅動馬達定向運動提供需要的能量,使系統偏離熱力學平衡狀態.研究表明,布朗馬達產生定向運動的物理本質在于:非對稱周期勢和非平衡漲落的共同作用,使得一定溫度下的布朗粒子向前和向后擴散的幾率不同, 從而產生定向運動.
Visscher和Block等人[8]在單分子實驗中發現驅動馬達以8.2nm左右的固定步長定向行走,同時也具有一定的隨機性,驅動馬達的速度隨負載力的增加而減小,馬達每行走1步催化水解1個ATP分子,說明驅動馬達的機械運動和化學反應是緊密耦合的。因此,在本文中我們在非對稱周期勢中考慮驅動馬達的機械化學耦合,基于布朗馬達的工作原理,利用MATLAB數值模擬驅動馬達在一定實驗條件下的運動特征.本研究可以為統計物理教學提供一個有趣的實例,同時為大學生利用物理規律解決實際問題提供可以借鑒的思路和方法[9].
1 機械化學耦合模型
1.1 ATP水解反應產生的自由能與活化能勢壘E
單分子生化實驗表明驅動馬達每行走1步催化水解1個ATP分子,ATP水解為ADP和磷酸根Pi的化學反應方程式為[8]

(1)
水解產生自由能為
(2)
其中,ΔG0是水解平衡值,ΔG和ΔG0的單位均為(pN·nm),[…]表示反應物和產物的濃度,實驗溫度為25℃(kBT~4.1pN·nm)條件下,ΔG0=55 pN·nm為一個常數,并保證溶液中[ADP]和[Pi]的濃度值為0.01μM·L-1.實驗測量表明,驅動馬達能夠利用一半的水解自由能來產生定向運動,我們將這部分自由能稱為有效自由能ΔGu,單位為(pN·nm),有效自由能ΔGu的表達式為
ΔGu=(27.5+2.05ln(104[ATP])) pN·nm
(3)
化學反應速率常數與[ATP]之間關系的Michaelis-Menten表達式[8]:
(4)
其中,KM是米氏常數,kmax是高濃度ATP下的水解反應速率常數.化學反應的實質是舊鍵的斷裂和新鍵的形成,ATP水解首先需要打開ATP分子中的共價磷酸鍵,這一過程需要吸收熱漲落提供的能量來克服活化能勢壘E.Kramers 理論給出了這個過程的反應速率常數與溫度的關系[10]:
(5)
其中,k0是阿倫尼烏斯常數.那么式(4)中的kmax可以寫為
(6)
其中,E0=1 pN·nm.結合式(4)、(5)、(6), 可以得到活化能勢壘E與[ATP]的關系式:
(7)
1.2 非對稱周期勢
由于驅動馬達的機械化學耦合,當行走中的驅動馬達處于ATP水解反應的不同化學狀態時,驅動馬達與軌道相互作用勢也不同,因此,我們引入中包含ATP水解反應中的活化能勢壘E以及有效自由能ΔGu的非對稱周期勢V(x),如圖1所示.
(8)
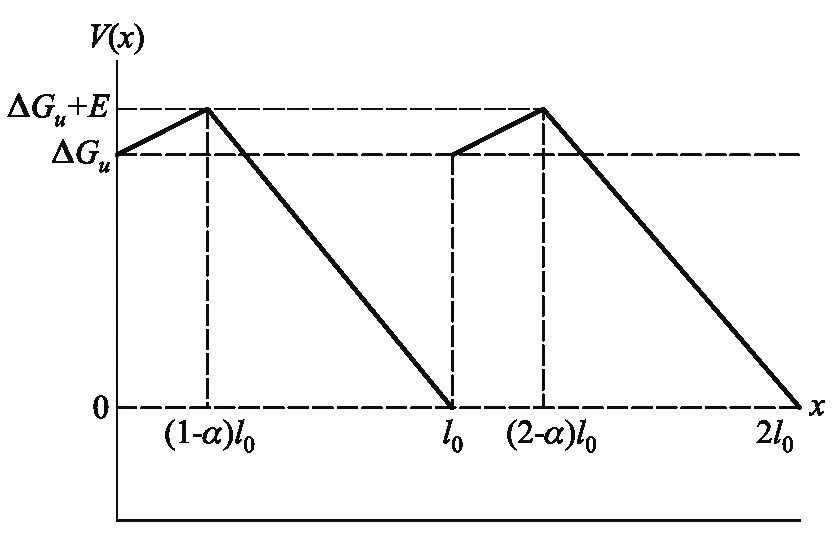
圖1 驅動馬達與軌道相互作用的非對稱周期勢(m=0,1)
周期勢以步長l0為周期,參數(1-α)表示化學反應對應的空間步長比例,即在((1-α)l0) 的步長空間里,驅動蛋白吸收熱噪聲提供的能量來克服活化勢E,并發生化學反應, 這個過程驅動馬達的速率幾乎為零,因此我們稱之為等待態.只有成功克服勢壘的驅動馬達才能產生定向運動,進入行走狀態.由此可見,驅動馬達與軌道相互作用的非對稱周期勢V(x)反映了驅動馬達行走中的機械化學耦合.
1.3 驅動馬達的運動模型
用過阻尼朗之萬方程描述驅動馬達在非對稱周期勢V(x)中的運動[11]:
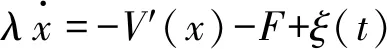
(9)
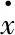
<ξ(t)>=0,
<ξ(t)ξ(t′)>=2Pδ(t-t′),
P=λkBT
(10)
2 結果與討論
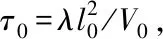
(11)
其中
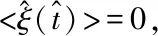
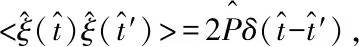
(12)
我們選擇與實驗中相同參數[8]:λ=8.00×10-3pNs·nm-1、α=7.30×10-1、KM=1.02×103μM·L-1、[ATP]=2.00×103μM·L-1、F=6.50 pN、l0=8.20 nm.借助MATLAB模擬了1000個粒子的運動.首先我們得到驅動馬達的位移隨時間的變化圖像,如圖2(a)和(b)所示.
從圖2(a)中能看到呈階梯狀的位移軌跡,為了仔細觀察驅動馬達的運動情況,我們將某一段位移-時間圖像放大后得到圖2(b),可以清晰看出驅動馬達的運動步長接近8.2 nm(圖中標出的兩組數據對應的Y軸坐標差值約為步長周期的2倍).驅動馬達每行進一步都會停留一段時間,如圖2(b)中對應的平臺所示,可以理解為這段時間是驅動馬達吸收熱噪聲提供的能量來克服活化勢E的過程,對應于非對稱周期勢(圖1)中((1-α)l0) 部分的等待態.由于熱漲落在這個過程中的起主導作用,馬達運動具有一定的隨機性.同時,可以觀察到圖2(b)中相鄰平臺之間的階梯,為驅動馬達將ATP水解產生的能量轉化為機械能的過程,這一階段驅動馬達克服活化勢壘后,產生了定向運動,對應非對稱周期勢(圖1)中(αl0) 部分的行走態.模型結果表明驅動馬達的運動是由等待態和行走態組成的,與Visscher和Block實驗中觀察到的結果吻合[8].為進一步研究驅動馬達的運動我們計算了驅動馬達的速率,如圖3(a)和圖3(b)所示.
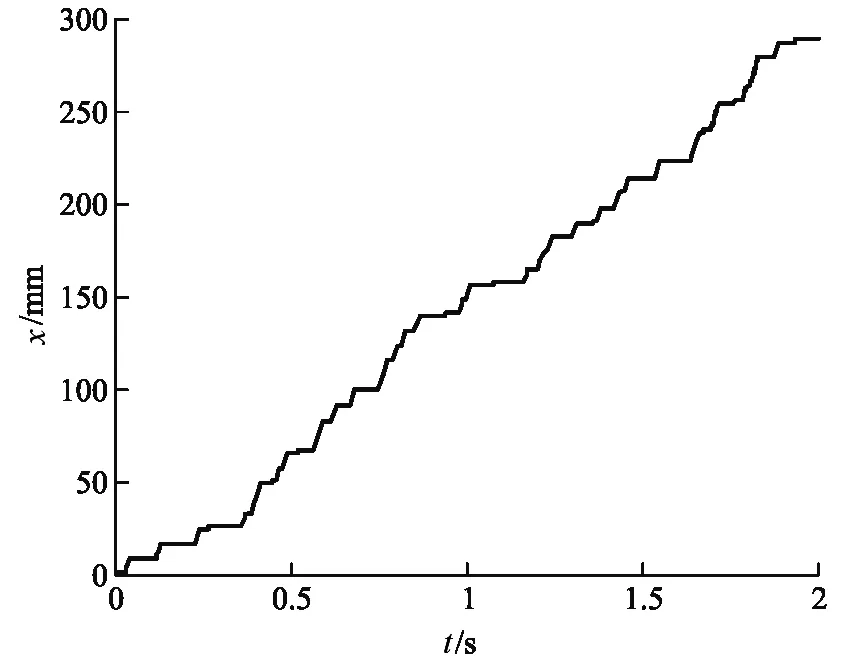
單個驅動馬達x-t圖
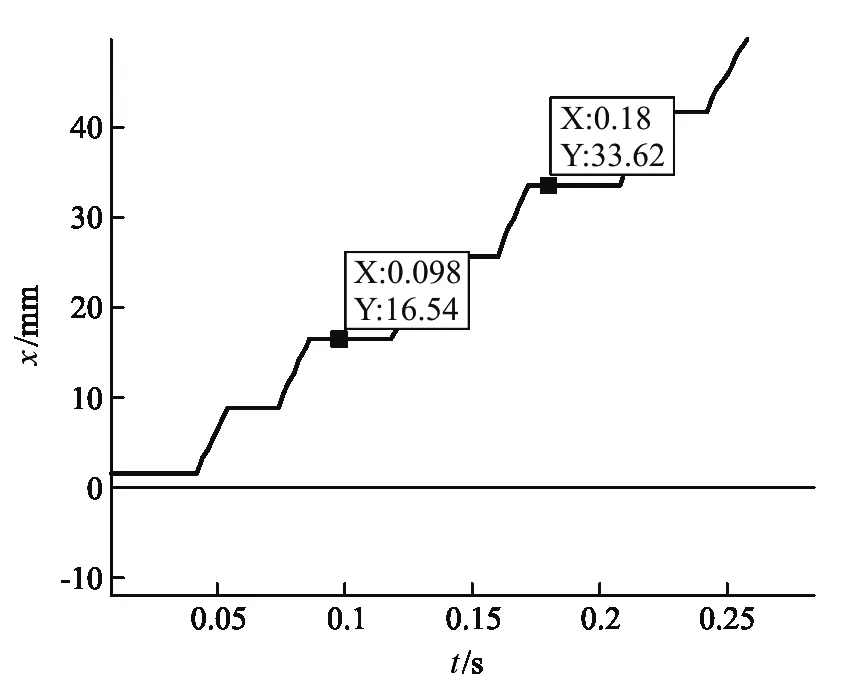
圖示(a)的放大圖2
在圖3(a)中,單個驅動馬達的速率隨時間的變化體現了驅動馬達具有行走和等待的“兩態”,速率大小的漲落表明運動具有隨機性.在圖3(b)中,我們分別計算n個驅動馬達的平均速率
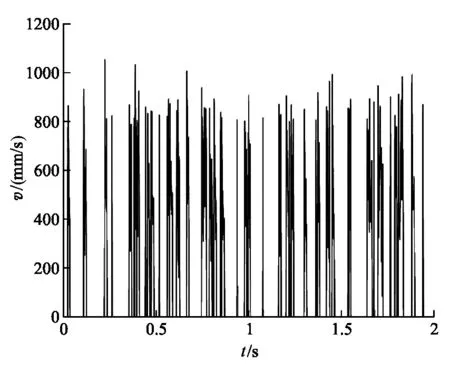
單個驅動馬達v-t圖
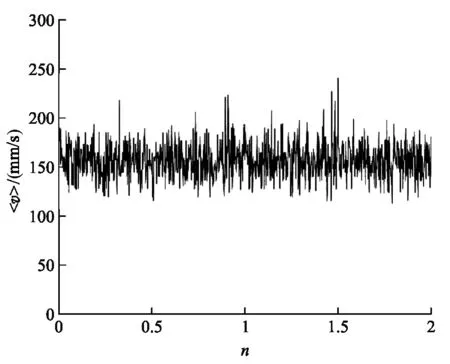
n個不同驅動馬達的平均速率圖圖3
為了研究負載力對驅動馬達運動的影響,考慮驅動馬達運動的隨機性,我們在不同負載力下,先分別計算n個驅動馬達運動速度的時間平均,然后計算n個驅動馬達運動速度的系綜平均隨負載力的變化圖像,如圖4所示.
從圖4中,可以看出驅動馬達運動速度的系綜平均值隨負載力F的增大而逐漸減小,同樣與實驗觀察的結果[8]相吻合.
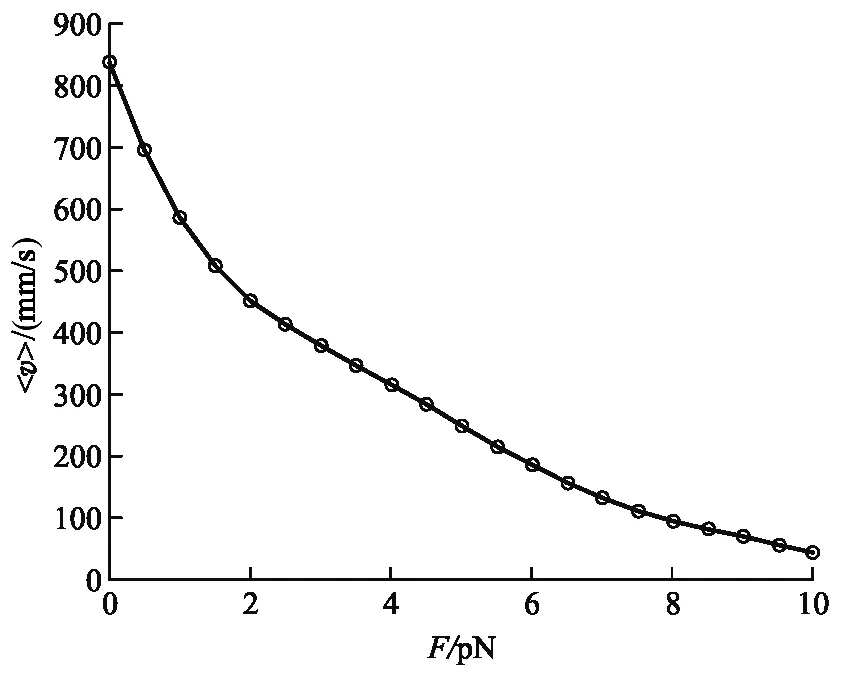
圖4 驅動馬達運動的系綜平均速度與F關系圖
3 結論
本文以非平衡態隨機動力學方程和驅動馬達運動的相關生化原理為基礎,在非對稱周期勢中體現驅動馬達運動過程中的機械化學耦合,并數值模擬得到相關圖像.將模擬圖像與實驗結果進行對比,驗證了驅動馬達的運動具有定向性、固定步長和一定隨機性的特點,表明所用模型的合理性.

