固體物理教學的若干思考Ⅱ：磁學前沿案例

袁 喆

(北京師范大學 物理學系，北京 100875)

固體物理是物理學高等教育中極為重要的一門專業課程.它既包含了晶格振動、能帶理論等基礎知識，也緊密結合凝聚態物理中的半導體物理、超導電性、磁學、表面與低維物理等分支學科的研究前沿，可以作為高年級本科生了解科研動態的一個重要的途徑[1,2].教學中引入科學研究的前沿進展可以激發學生的學習熱情，并鍛煉學生運用課程前半部分學習的基礎知識去解決實際科學問題的能力，從課程教學自身角度來說就已是非常必要.

教育部高等教育司在《2019年教育部高等教育司工作要點》中提出實施一流課程的“雙萬計劃”，統籌規劃國家級和省級一流課程的培育與建設，打造具有高階性、創新性、挑戰度的“金課”[3,4].對于固體物理來說，高階性是天然存在的，固體物理課程涉及的知識面較廣，涵蓋了四大力學，而它主要是應用量子力學、統計物理等課程的知識解決晶體物理性質等實際問題，是促進物理專業學生知識、能力、素質有機融合的理想平臺，也可以充分培養學生解決復雜問題的綜合能力和高級思維.凝聚態物理學的多個分支學科，例如超導、磁學、表面與低維物理等仍然處于高速發展的過程中，因此課程內容的創新性要充分反映科學前沿成果和發展方向，同時也自然地保證了學習內容的探究性和教學形式的互動性.教學中引入科學發展的前沿，對教師備課和學生課內外的學習提出了更高的要求，在很大程度上提高了課程的挑戰度.

總的來說，固體物理課程與金課的“兩性一度”的要求高度契合，落實的關鍵在于是否能夠找到合適的前沿課題作為切入點：太過深入或者需要較多知識準備的學術問題并不適合面向本科生的教學，而發展得足夠成熟到能夠寫入教科書的內容也往往不再是前沿研究內容，也是不合適的.找到合適的前沿研究案例融入固體物理教學，要求授課教師必須深刻理解科研動態，并有能力將其轉化為本科階段能夠掌握的形式展示給學生.

本文聚焦于固體物理的磁性章節，從近年來自旋電子學領域研究的磁疇壁賽道存儲器入手，通過探討磁疇和磁疇壁的產生原因引入鐵磁材料中相互作用的物理機制和特點.再以磁疇壁電阻為例，討論自旋相關輸運的問題，特別是和固體物理前面幾章學習的布洛赫電子態、輸運過程等內容結合起來，達到融會貫通的效果.希望這個典型案例能夠為從事固體物理教學的教師們提供借鑒與參考.

1 從磁疇壁賽道存儲器引出磁性材料中的相互作用

磁疇壁賽道存儲器基于自旋轉移力矩[5,6]的概念和電流驅動磁疇壁運動[7]的物理過程，由Stuart Parkin在2008年提出[8].它的載體是一條條鐵磁金屬納米線，其中包含了一系列具有相反方向磁矩的磁疇單元，用來編碼0和1.施加電流可以推動這些磁疇單元在納米線中整體平移，任意一個單元都可以移動到固定的讀寫頭附近，進行讀寫操作.與傳統的磁性硬盤相比，磁疇壁賽道存儲器的運行僅改變磁矩方向，不存在機械運動過程，因此在運行速度和能耗方面具有更優的潛力，且可能實現三維高存儲密度集成，是近年來自旋電子學領域的重點研究方向之一.

通過對磁疇壁賽道存儲器的介紹，可以看出磁性材料由于具有南北極的磁矩取向，是數字存儲的天然媒介.因此自然地會想到如下幾個問題：1) 磁有序的物理起源是什么？2) 磁存儲器中數據單元是否穩定？3) 使用什么材料能夠提高數據存儲密度？這幾個問題的答案就包含在磁性材料的基本相互作用中.

在教學中，可以利用對磁疇壁賽道存儲器的介紹和上述問題，切入鐵磁性的基本內容.通常從海特勒-倫敦理論出發，推導出交換相互作用和海森堡模型[9].鐵磁交換相互作用讓磁矩趨向于一致排列，此時在晶體外部會產生較高的靜磁能.這種較強的短程交換相互作用與較弱的長程靜磁(磁偶極)相互作用的競爭，導致了磁體通常分割成許多微米尺度的磁疇.在磁疇的內部，磁化強度取向一致，朝向能量最低的易磁化軸方向.而易磁化軸的方向取決于各向異性能，包括源于自旋軌道耦合相互作用的磁晶各向異性能和源于靜磁相互作用的形狀各向異性能.各向異性能的存在使磁化強度從一個能量最低的方向翻轉到另一個能量極小方向時必須跨過能量勢壘，當這個勢壘的高度遠大于室溫(kBT≈26 meV)就保證了數據的穩定性.為了實現數據的高密度存儲，需要降低磁疇和磁疇壁的尺寸.磁疇壁是不同磁疇之間的過渡區域，其中磁化強度方向逐漸從一個磁疇的方向轉到另一個方向[10].磁疇壁的尺寸由交換能和各向異性能競爭所決定，交換能占優勢的材料中，磁化強度的梯度較小，導致較寬的磁疇壁.而各向異性能較強的材料中磁化強度盡可能沿著易軸方向，因此較大的各向異性能會顯著降低磁疇壁的寬度.

綜上所述，通過磁疇和磁疇壁的物理機制，完整地展示出鐵磁材料中的三種最為重要的相互作用：交換能、靜磁能、各向異性能，以及它們之間的相互競爭與妥協的效果.這些基本知識內容，大部分教科書上都有涉及[9-12]，在此不贅述.

2 磁疇壁中的自旋相關輸運

固體的磁性一般作為一個專題章節，放置于晶體的布洛赫電子論、輸運現象和晶格振動等基礎知識之后.上一節僅把研究前沿作為切入鐵磁性教學內容的引子，本節的內容則利用電子論和輸運過程等固體物理的基礎知識來處理一個具體的自旋相關輸運問題，即磁疇壁的存在對鐵磁金屬電阻的影響.

自基泰爾于上世紀40年代建立磁疇理論起，磁疇壁對鐵磁金屬電阻或電阻率的貢獻就一直為研究人員所關注.在很長一段時間里，受實驗條件的限制，磁疇壁電阻僅局限于理論研究[13].直到上世紀90年代才實現了第一次定量的測量.Gregg等人制備了具有條紋磁疇的鈷薄膜，易軸垂直于薄膜平面，施加垂直薄膜方向的外磁場會消除部分磁疇，即減少磁疇壁個數，此時測得薄膜的電阻率變小，說明磁疇壁存在會增加電阻率[14].但隨后也有其它實驗得出相反的結論[15]，引發了磁學領域熱烈的討論.

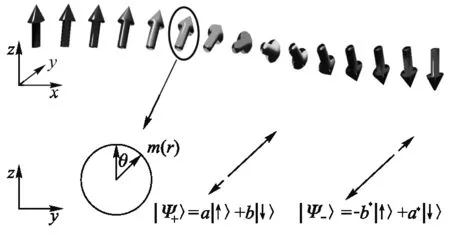
圖1 上圖：布洛赫型磁疇壁示意.下圖：磁疇壁中局域磁化強度轉角定義，電子波函數混合了向上和向下自旋分量.

2.1 磁疇壁中的電子態

磁疇壁最主要的特征是非共線的磁化強度.在共線磁性材料中，如果自旋軌道耦合較弱，可以近似認為自旋角動量守恒，不同自旋的電子態彼此獨立.磁疇壁的非共線磁化自然地混合自旋向上和向下電子態，使自旋不再是一個好量子數.不失一般性，考慮一個布洛赫型磁疇壁，其構型如圖1所示.局域磁化強度方向可以寫作m(r)=[0,sinθ(x),cosθ(x)]，用一個幺正矩陣：

(1)

可以把定義在笛卡爾坐標系的自旋分量σ·m(r)變換到局域量子化軸下定義的σz，即U-1σ·mU=σz.由于磁疇壁中局域量子化軸的方向隨位置x變化，每一處的電子態受周圍與其非共線磁化方向上電子態的影響，會產生自旋的混合.這是因為幺正變換U與哈密頓量中的動能項不對易[16]，

(2)

對于非常寬的磁疇壁，?θ/?x很小，式(2)中的后兩項可以看做微擾，保留頭階項，得到微擾強度正比于磁化強度的梯度，即正比于磁疇壁寬度λ的倒數.此時哈密頓量的本征態不是局域量子化軸下的純自旋態，而可以寫作：

|Ψ+〉=a|↑〉+b|↓〉

(3)

|Ψ-〉=-b*|↑〉+a*|↓〉

(4)

其中b是正比于1/λ的小量，|b|<<|a|.注意到上述微擾圖像的結論是普適的，與具體的θ(x)函數形式無關.考慮一種被稱為自旋螺旋(spin spiral)的特殊結構，即?θ/?x是常數，其電子本征態可以嚴格求解，電子態的總自旋相對局域量子化軸總是存在一個常數偏角[17].

2.2 布洛赫型磁疇壁對傳導電子的散射

固體材料中總是存在各種無序，例如雜質原子、晶格缺陷、原子振動和磁矩漲落等.后兩者甚至在極低溫下依然由于零點振動和量子漲落而無法完全消除.晶格中的布洛赫電子態被這些無序散射導致有限的電阻率.結合輸運理論，可以寫出磁疇壁中布洛赫電子態的散射幾率，假定散射勢的形式為

(5)

式(3)和式(4)中布洛赫電子的弛豫時間可以通過量子力學含時微擾論中費米黃金定則來計算.如果只考慮彈性散射，即散射前后傳導電子能量不變，均保持在費米能量上，則弛豫時間的具體形式可以寫作

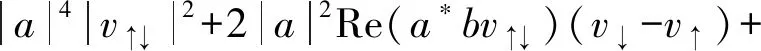
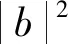
(6)

由于磁化梯度的影響反映在參數b中，通過考察b的冪次項來討論磁疇壁對弛豫時間的影響.式(6)中所有弛豫時間倒數中，頭階展開項都是b的線性項，次階為b的平方項.考慮到b與疇壁寬度λ成反比，磁疇壁的電阻率可以表示為

(7)

其中ρ0是共線磁化材料(即無磁疇壁時)的電阻率，C1和C2是材料相關的系數，與磁化梯度或疇壁寬度無關.

2.3 與磁疇壁寬度無關的常數電阻

由于磁疇壁電阻R(λ)∝λρ(λ)，結合式(7)可知，對于一塊具體的磁性金屬材料，磁疇壁的存在會產生一個與疇壁寬度無關的電阻項和另一個與疇壁寬度成反比的項，即

(8)

在疇壁非常寬的極限下，最后一項可以忽略，只剩下一個常數項R1.這個結論與我們的直覺不大一致，通常認為當磁化梯度變得無限小，則電子輸運性質會等同于共線磁化的情況.而式(6)給出的結論是：無論一個磁疇壁有多寬，總會多出一個常數電阻，并且這個常數電阻與磁化梯度的具體形式θ(x)無關.

接下來討論這個常數電阻的物理來源.注意到式(6)中b的線性項中均包含因子v↑↓，即散射勢式(1)中的非對角矩陣元，因此b的線性項都來源于局域量子化軸下自旋翻轉的散射，而這需要自旋軌道耦合來提供改變傳導電子自旋的角動量.最終可以得出結論，自旋軌道耦合導致自旋翻轉的散射，從而使磁疇壁貢獻一個與寬度無關的常數電阻R1，可以稱之為絕熱磁疇壁電阻.在自旋軌道耦合可以忽略的情況下，磁疇壁導致的電阻與疇壁寬度成反比，此時非常寬的磁疇壁可以近似等價于共線磁化的金屬.上述結論與第一性原理輸運計算得到的坡莫合金(Ni80Fe20)磁疇壁電阻完全一致[18]，其中絕熱磁疇壁電阻R1的數值約為0.1×10-15Ωm2.

2.4 窄磁疇壁電阻的來源

在較窄的磁疇壁中，可以得到隨磁疇壁寬度減小而急劇增大的電阻R2/λ.這部分電阻來源于式(6)中b的二次項，僅與散射勢的對角元有關，因此是自旋角動量守恒的散射過程所貢獻.過渡金屬和合金中的電子自旋擴散長度一般為幾納米到幾十納米的尺度[19]，在這個長度范圍內傳導電子保持自旋方向不變，因此當磁疇壁寬度小于或接近自旋擴散長度時，大多數電子在通過磁疇壁前后保持自旋守恒，如圖2所示.由于疇壁兩側磁疇方向相反，入射電子透過磁疇壁后，多數自旋載流子變成了少數自旋載流子，因此費米面上的態密度減少了，從而引起部分電子被反射，增大了電阻.這一過程和磁性隧道結中的隧穿磁電阻效應[11]非常類似，即反平行構型下的隧穿電阻總是要大于平行構型下的電阻，且兩者的比例通常取決于鐵磁材料費米面電子的極化(兩種自旋的比例).

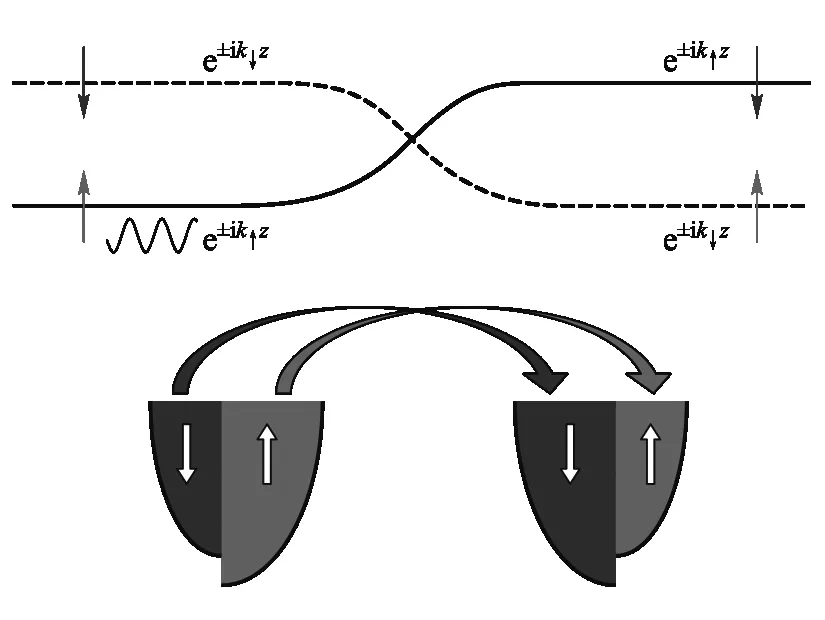
圖2 電子通過窄磁疇壁前后自旋守恒散射過程.入射的多數自旋載流子在通過疇壁后成為少數自旋載流子，該過程類似磁性隧道結中的自旋相關隧穿效應，隧道結兩側磁化強度的反平行排列導致更多入射電子被反射，電阻增大.

在窄磁疇壁中由于較大磁化梯度產生的電阻隨疇壁寬度的增加而逐步減少.這是因為當疇壁寬度逐漸增大，有更多的電子跟隨局域磁化的方向逐步改變自旋方向，即入射時為多數自旋載流子，透射后仍然是多數自旋載流子.當磁疇壁寬度遠大于自旋擴散長度時(λ→∞)，幾乎所有電子都可以完全跟隨局域磁化方向，則由窄疇壁的自旋守恒透射產生的這部分電阻就消失了.

3 奈爾型磁疇壁中各向異性磁電阻的貢獻

當電流穿越布洛赫型磁疇壁時，電流方向與局域磁化的方向始終是垂直的.對于奈爾型磁疇壁，這個關系就不再成立了，如圖3所示，若電流流過一個尾對尾奈爾型磁疇壁：

(9)

電流與局域磁化的方向在左右兩端是平行(反平行)關系，而在疇壁中間是相互垂直的.旋轉奈爾型磁疇壁：

(10)

也存在磁化強度與電流相互平行和相互垂直的區域.此時必須考慮到磁性材料中的各向異性磁電阻效應(Anisotropic magnetoresistance，簡稱AMR)[20].該效應也是自旋軌道耦合的結果，在大部分鐵磁金屬與合金中，當磁化強度與電流方向平行(反平行)時，電阻率ρ‖會比兩者相互垂直時的電阻率ρ⊥大一些.對于坡莫合金，兩者的差別在低溫下大約能達到20%，室溫下約4%左右.

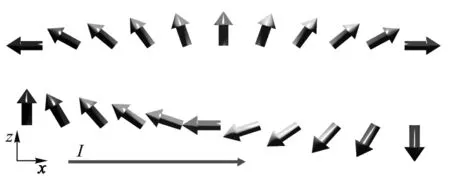
圖3 奈爾型磁疇壁(上圖)和旋轉奈爾型磁疇壁(下圖)示意.電流始終沿磁疇壁方向.

各向異性磁電阻的存在使奈爾型磁疇壁區域電阻率更低，因此磁疇壁的存在會降低鐵磁金屬的總電阻，且奈爾型疇壁越寬，電阻降低越多.旋轉奈爾型磁疇壁中間的電阻率更大，因此該類型疇壁越寬，電阻越大.下面定量計算各向異性磁電阻貢獻的磁疇壁電阻，一般來說，對于多晶或各項同性鐵磁金屬，局域電阻率可以寫成

ρ(x)=ρ⊥+(ρ‖-ρ⊥)cos2φ(x)

(11)

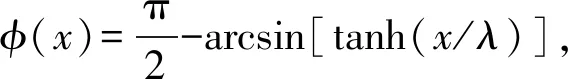
(12)

AMR在奈爾型磁疇壁中產生的電阻可以解析計算(假設體系長度遠大于磁疇壁寬度，L>>λ)：

(13)

使用同樣的方法，可以計算出旋轉奈爾型磁疇壁中的AMR會貢獻一個正的電阻為

(14)

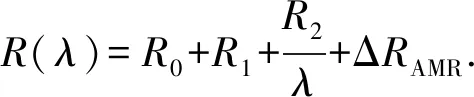
4 小結

固體物理的教學有必要融入最新研究成果，使課程內容反映前沿性和時代性，以達到培養物理專業學生解決復雜問題的綜合能力.同時對于前沿案例的選擇必須充分考慮學生的知識基礎，鼓勵學生有勇氣去探究前沿科學問題，培養學生面對未知領域的創新能力.這也正體現了打造金課的“高階性、創新性、挑戰度”這一要求.

作為一個典型案例，本文介紹了如何通過磁疇壁賽道存儲器引入鐵磁性材料中的基本相互作用等教學內容，并進一步選擇了磁疇壁電阻這一自旋電子學領域的研究前沿，讓本科生在學習固體的磁性章節時，能夠結合已掌握的電子能帶論、輸運現象和量子力學微擾論等內容，自主地探討磁性金屬材料中自旋相關輸運現象.通過對電子自旋態和無序散射導致的弛豫時間的分析，發現磁疇壁貢獻的電阻與疇壁寬度的關系.在討論過程中，主要基于物理圖像做定性分析，避免冗長的嚴格計算，把數學表達式中隱含的物理過程揭示出來，例如散射勢中的非對角元對應自旋翻轉散射，自旋翻轉散射和自旋守恒散射分別會導致一個與磁疇壁寬度無關的常數電阻和一個與磁疇壁寬度成反比的電阻.后一過程與磁性隧道結中的隧穿磁電阻效應的物理圖像是一致的.各向異性磁電阻效應對于非布洛赫型磁疇壁會貢獻一個與疇壁寬度成正比的電阻，可以是正值或負值.

致謝：本文的寫作得到了北京師范大學物理學系馬嘯云和高著同學的大力幫助.