基于正交移動雙水下自主潛航器的水下合作目標定位方法

趙 晨 喬 鋼 周 鋒

(哈爾濱工程大學水聲技術重點實驗室 哈爾濱 150001)

(工業和信息化部海洋信息獲取與安全工信部重點實驗室(哈爾濱工程大學) 哈爾濱 150001)

(哈爾濱工程大學水聲工程學院 哈爾濱 150001)

1 引言

近年來，隨著水聲及無線通信技術的發展，水下傳感器網絡在海洋資源開發，水下環境獲取，水下目標探測等領域具有越來越重要的作用[1,2]。隨著水聲通信技術的不斷進步，基于水聲通信網絡中的目標定位方法也成為了水聲技術研究的熱點課題[3]。

大范圍水下目標定位常用于遠海，深海目標定位，具有較大的應用背景，是水聲定位研究的主要方向之一[4]。傳統大范圍水下目標定位方法，利用水下傳感器組網實現定位。基于水下傳感器網絡的定位方法，需要利用布置在海底的潛標節點作為錨點，利用目標與錨點之間的通信完成定位過程。通常采用目標與節點間的信號傳播時延測量(Time-Of-Arrival, TOA)或信號傳播時延差(Time Difference Of Arrival, TDOA)的測距定位方法，或者利用測量目標到各個接收信號之間的方位角(Angle Of Arrival, AOA)和利用多跳信標間通信(DVHop)的非測距定位方法[5–7]。在大范圍海域中，通過增加網絡中通信節點個數，可以有效擴大定位覆蓋范圍[8]。該種方法在定位范圍增加的情況下，通信節點個數需要成倍數地增長，并且需要在定位前布置好水下節點的位置，不利于未知區域定位和隱蔽定位。另一種常規方法采用區域劃分，對定位區域進行劃分，每個區域內，利用水面甲板單元攜帶的大型超短基線基陣，對目標進行定位[9]。該方案對設備要求較高，定位過程耗時長，并且不適用于深遠海目標定位。

近年來隨著水下導航技術和移動傳感器技術的不斷發展，水下無人潛航器(Untethered Underwater Vehicle, UUV),水下自主潛航器(Autonomous Underwater Vehicle, AUV)和水下機器人(Remotely Operated Vehicle, ROV)有了越來越多的應用場景[10,11]。基于移動傳感器的目標定位方法是水聲定位技術的一個新的研究方向。現有水下移動節點通常載體上攜帶慣性導航系統( Inertial Navigation System, INS)，多普勒速度計(Doppler Velocity Log, DVL)和陀螺儀等設備，可以較為精確地計算出自身在水下的導航位置[12,13]。以AUV定位為例，相較于傳統的基于多信標測距的長基線定位方法，采用這種定位方法對水下載體定位時只需要利用少量AUV對目標進行定位，占用資源少，具有重要的應用價值[14,15]。

目前，一些基于AUV的定位方法也被逐漸提出，文獻[16]中提到了一種基于虛擬長基線定位單AUV定位方法，該方法利用一個固定在水下的潛標節點，和一個具有導航裝置的AUV，利用聲信號傳播的時間可以確定目標與海底聲信標之間的距離。通過AUV的多次運動，建立虛擬水下潛標節點，實現虛擬信標定位。但該方法需要借助海底潛標節點進行輔助定位，并且至少需要3次以上AUV運動才可以確定目標位置。文獻[17]中，針對AUV定位中區域聲速不同問題，提出了一種利用卡爾曼濾波器進行彎曲補償的改進方法，有效地降低了定位過程中聲速誤差對定位結果的影響，提高定位精度，但該方法對節點間的時間同步要求較高。

針對單AUV目標定位中存在的單次定位過程中通信次數長和時間同步問題，本文提出了一種基于正交運動的雙AUV定位方法，利用兩個運動航向角呈90°的AUV完成定位。定位過程中靜止目標通過測量到每個AUV間的通信時延差，進行雙曲定位。有效降低了定位的同步誤差，并且降低定位過程中的通信次數。

2 基于單移動AUV靜止目標定位方法

基于單AUV的移動定位方法，利用AUV移動過程中，測量多次通信間隔中待定位靜止目標收到來自AUV的信號到達時間實現定位，定位原理如圖1所示。

通常每個AUV可以利用攜帶的慣性導航系統和陀螺儀測得自身航跡位置。AUV運動姿態由航向角，俯仰角和橫滾角描述，假設移動AUV航向角為Ψ，俯仰角為θ，橫滾角為φ，則AUV運動坐標系{B}與大地坐標系{L}之間的轉移矩陣RLB為[18,19]

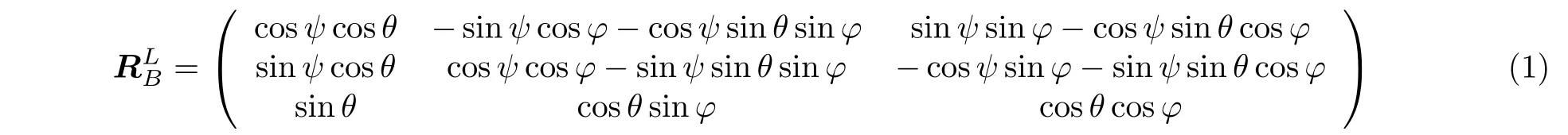
若AUV相對運動坐標系的移動速度為v，則經過t時刻AUV移動距離L為

初始位置已知時，AUV可以通過速度v和時間t計算自身坐標位置。通常AUV和靜止目標的深度信息可以通過壓力傳感器測量，靜止目標T (x, y)與AUV每次通信間間距li可以由聲速c和通信時間ti計算

根據球面交匯的幾何模型[3]，靜止目標經過最少3次與AUV之間的通信，可以計算自身位置。如

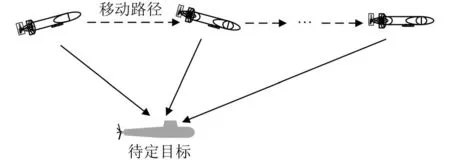
圖1 單移動AUV靜止目標定位示意圖

圖2所示，假設經過n次通信后，AUV每個通信位置記錄自身坐標分別為(x1, y1), (x2, y2), ···, (xi, yi)根據距離關系

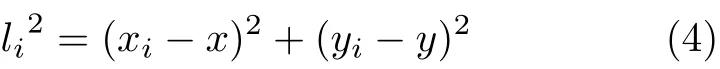
經過化簡并利用最小二乘法進行求解[20,21]，整理得到

基于單AUV移動的靜止目標定位方法，至少需要3次AUV與靜止目標間的通信實現定位。AUV移動路徑較長，由于AUV自身的INS系統的累積誤差，使得多次移動間AUV自身位置誤差增加，同時AUV與靜止目標間的時鐘同步存在誤差，導致單AUV靜止目標定位誤差較大。

3 基于正交移動AUV靜止目標定位方法

3.1 基于正交移動AUV算法實現

針對單移動AUV利用慣性導航系統對靜止目標多次通信間隔完成的定位誤差問題，本文提出了一種基于正交運動的AUV靜止目標定位方法，原理如圖3所示。

該定位方法由兩個運動路徑規劃互相呈90°的移動AUV實現。定位原理如圖4所示，假設2個AUV初始坐標標分別為A1(x1, y1), B1(x'1, y'1)，與待定位靜止目標距離分別為r1, d1，當聲速為c，靜止目標接收到A1與B1信號到達時間分別為t1和t'1，根據距離坐標關系，可以得到

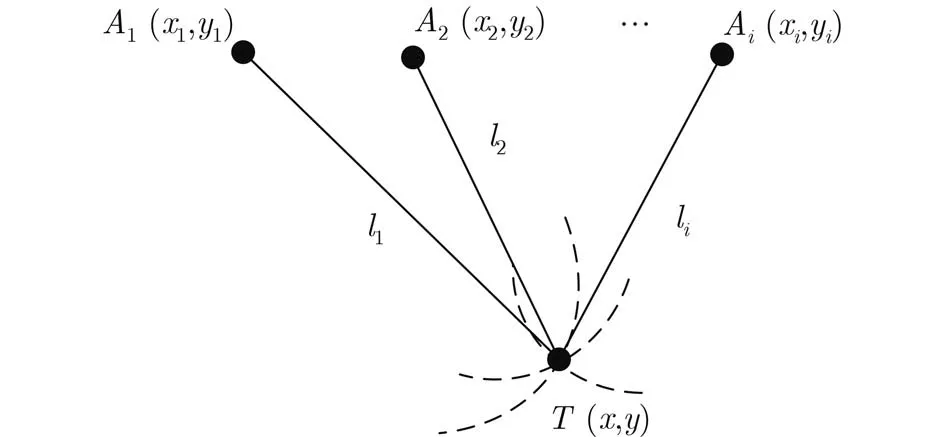
圖2 單移動AUV球面交匯算法原理示意圖

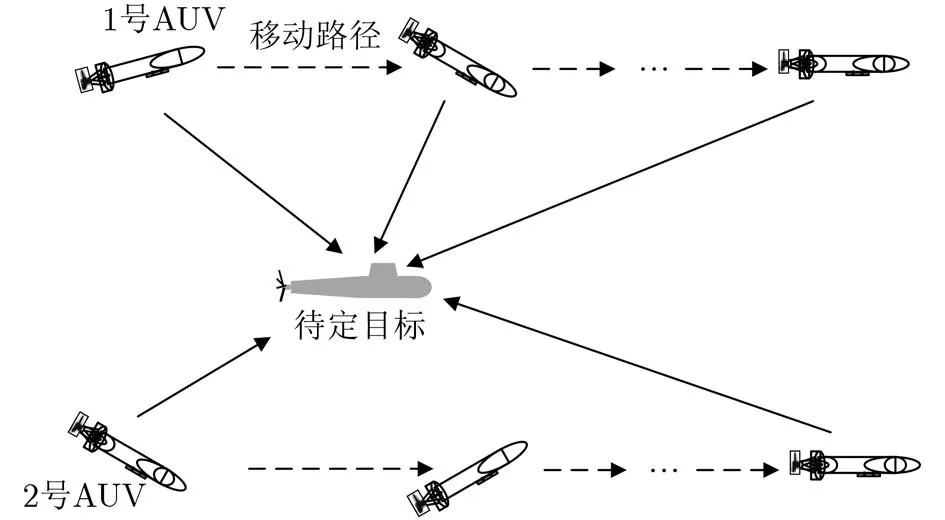
圖3 正交運動AUV靜止目標定位示意圖

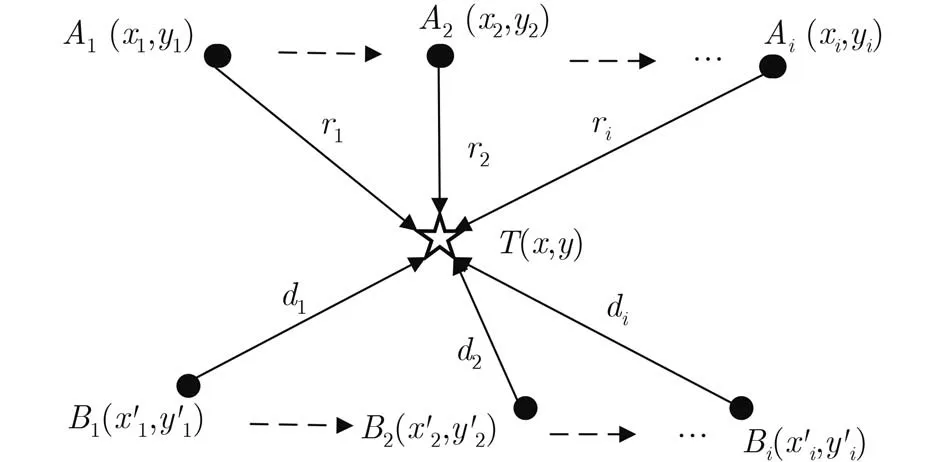
圖4 正交運動AUV定位算法原理示意圖

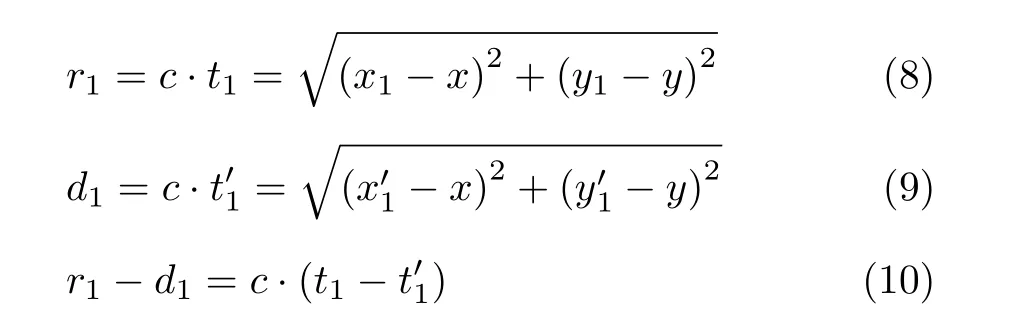
其中，t1– t'1為信號到達時延差。在經歷1次通信間隔后，AUV分別移動至坐標A2(x2, y2), B2(x'2,y'2)，靜止目標接收到A1與B1信號到達時間分別為t2和t'2，根據式(8)和式(9)，同理得到

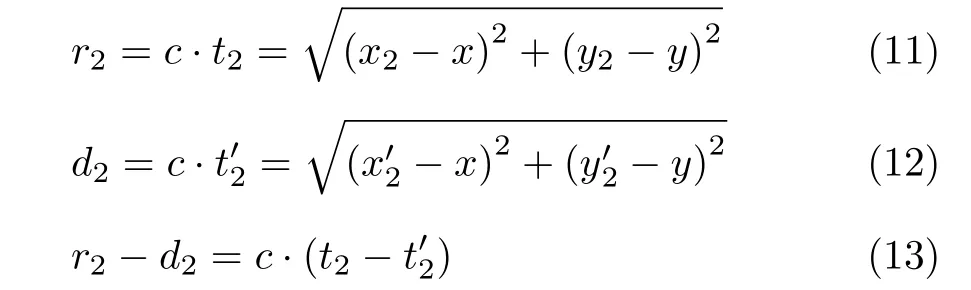
同理t2– t'2為靜止目標經歷1次通信間隔后接收到AUV信號的時延差。整理式(8)—式(13)，靜止目標與AUV之間的距離關系為

利用式(18)—式(20)待定位靜止目標最少可以通過每個AUV 1次運動過程和靜止目標間的2次通信，實現靜止目標定位。當AUV多次運動，再移動i–1個周期后兩個AUV分別移動至Ai(xi, yi),Bi(x'i, y'i)，則重復式(8)—式(20)推導步驟，同理可以計算經歷AUV i–1次運動后靜止目標位置為

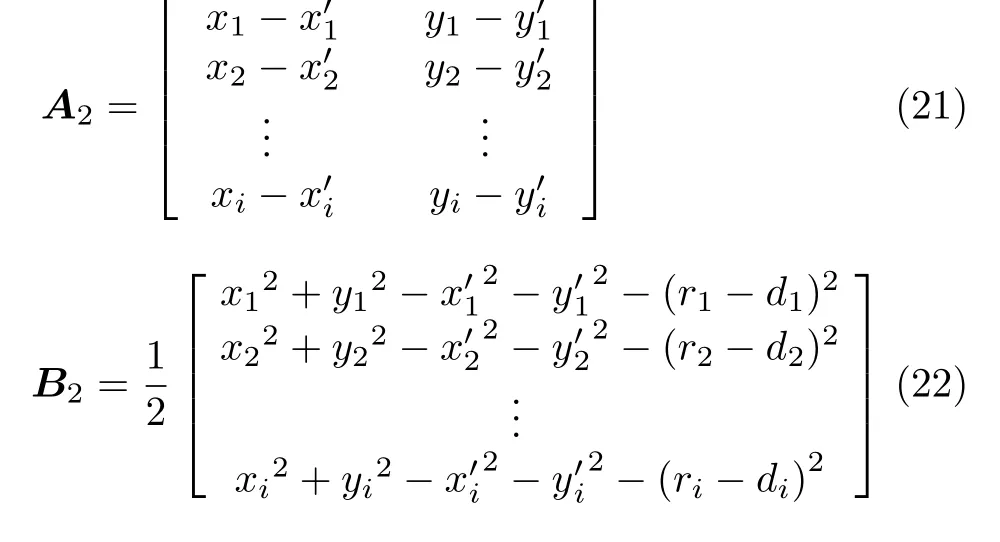
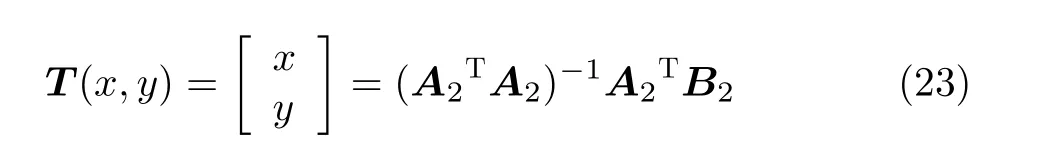
3.2 基于正交移動AUV定位過程實現

根據3.1節中的定位算法原理，本文設計了基于正交運動AUV定位方法。定位過程如圖5所示，首先每個AUV進行自身位置校準和AUV與靜止目標之間的時間同步校準。經過位置和時間校準后，AUV向靜止目標發射帶攜帶自身位置信息的通信信號，靜止目標接收到信號后，記每個AUV位置坐標和AUV傳輸信號的到達時延差。隨后AUV開始按照規劃路線進行運動，經歷1個時間周期后，通過自身INS系統確定所在位置，再將位置坐標通過通信信號發送給靜止目標，靜止目標記錄每個AUV坐標和發送信號的到達時延差。以此類推重復上述過程，再經歷i–1個AUV移動周期后，利用式(20)—式(22)即可解算出靜止目標所在位置。

正交運動AUV定位流程圖如圖5所示。

4 仿真分析

根據本文提出算法，分別對單AUV移動定位和正交AUV移動定位做出仿真實驗分析。仿真參數設置：定位范圍設定50×50 km，聲速c=1500 m/s,AUV的有效通信距離為10 km, AUV的運動速度為10 km/h, INS導航系統的平均累積誤差為2 m/km，信號測時誤差為100 ms，誤差均服從高斯分布。兩種定位方法中AUV的運動路線分別如圖6(a)和圖6(b)所示，其中橫坐標為地理東向坐標，縱坐標表示地理北向坐標。

4.1 仿真實驗1 區域定位誤差分布實驗

為了研究和比較單AUV移動定位方法和正交規劃移動AUV定位方法的精度，設計定區域定位誤差分布仿真，掃描區域50 km×50 km, AUV移動路按照圖6中移動路線分別從起點位置移動到終點，靜止目標掃描位置間隔為100 m，每個定位周期內靜止目標與每個AUV完成3次通信，每個定位點定位20次并計算定位結果的均方根誤差，仿真結果如圖7(a)和圖7(b)所示。根據仿真數據整理和統計，圖7(a)的定位均方根誤差最小值為103 m，中心區域平均誤差為112 m，邊緣區域最大誤差為165 m，圖7(b)的定位均方根誤差最小值為70 m，中心區域平均誤差為95 m，邊緣區域最大定位誤差為122 m。從圖7中可以看出，正交移動AUV的靜止目標定位方法，在精度上高于單AUV定位，并且其中藍色覆蓋區域明顯大于單AUV定位的覆蓋區域。

圖5 正交運動AUV定位流程圖

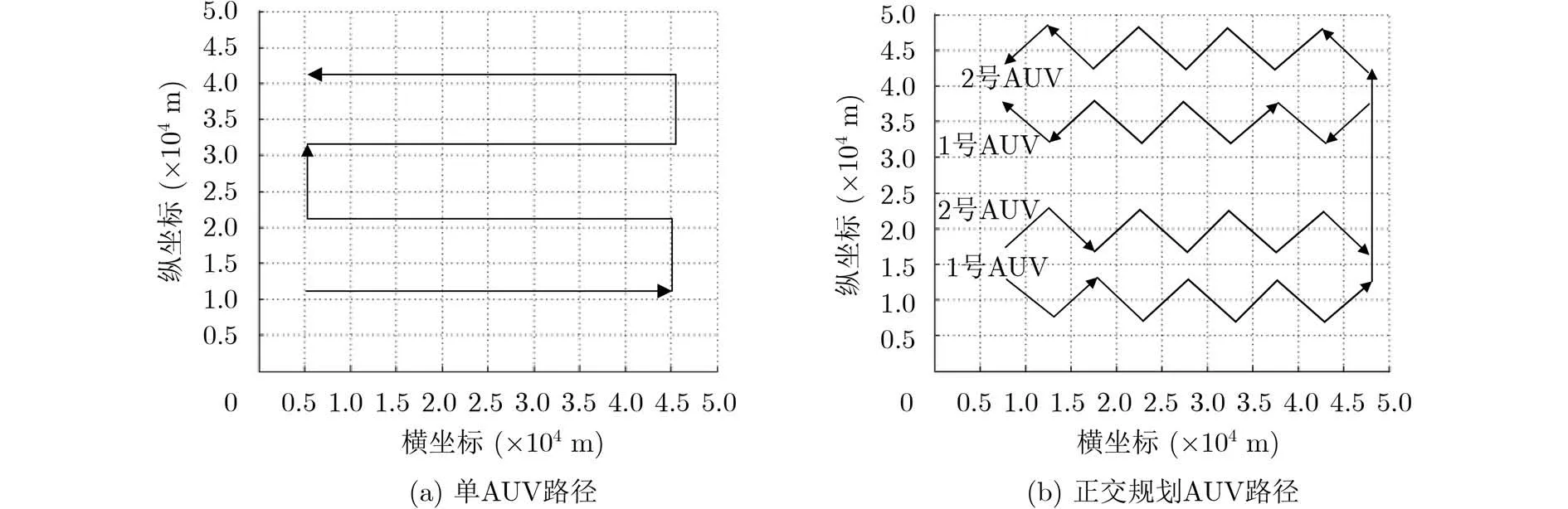
圖6 單AUV運動路徑規劃圖

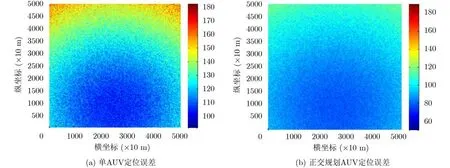
圖7 兩種定位方法定位誤差分布圖

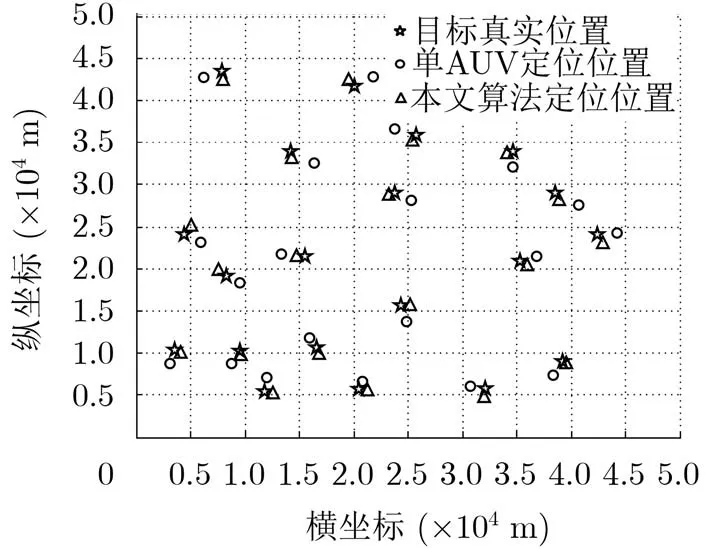
圖8 隨機位置靜止目標定位結果圖

為了進一步比較兩種定位算法的定位效果，在區域內選取20個隨機靜止目標位置，記錄真實位置，分別采用單AUV定位和正交運動的AUV定位方法實現定位，實驗結果見圖8。從圖8中可以看出，下方區域采用兩種方法的定位結果距離靜止目標真實位置較近，本文提出的方法相比于單AUV定位的定位誤差更小。隨著AUV按照路徑移動時間增加，導致INS系統的累積誤差增大，AUV自身位置存在誤差，圖8中上方區域定位結果距離靜止目標真實位置距離均有所增加，單AUV定位誤差增加較大，本文提出的方法誤差增加較小，并且定位結果優于單AUV定位。

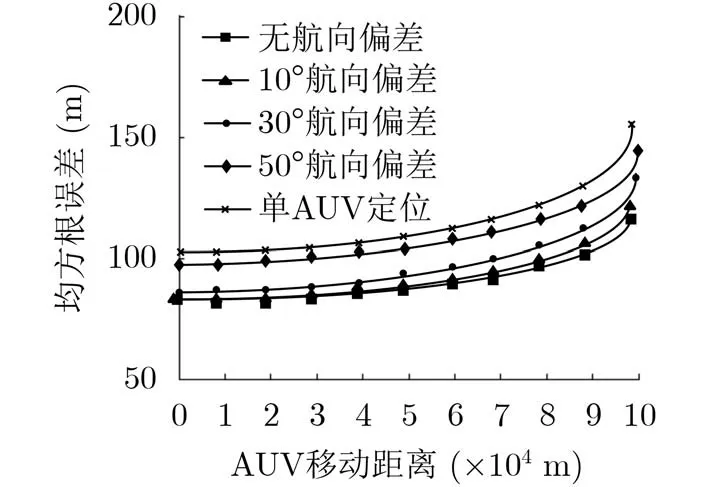
圖9 不同航向角定位誤差隨AUV移動距離變化關系圖

在實際應用中，由于受到洋流等海洋環境的影響，和AUV具體運動規劃的需求，在實際應用中難以保證AUV規劃路線的絕對正交。為了比較AUV導航誤差對兩種方法的影響，將圖7中每個AUV路徑的移動距離計算出，并與兩種定位方法的誤差值對應，并且分別引入10°, 30°和50°的航向偏差，結果見圖9。從圖9中可以看出，在AUV初始移動過程中，AUV自身導航誤差對兩種方法的定位結果影響不大。但隨著AUV移動距離不斷增加，每種方法的定位效果均有所下降。在正交運動AUV的航向角角度存在10°偏差時，定位效果與理想無航向角偏差情況效果相近，當航向角角度偏差增加到30°時，定位偏差有所增大，當航向角度存在50°偏差時，定位誤差增加較大。但每種方法的定位效果均優于單AUV定位。在不同航向角角度規劃的情況下，本文提出方法都有效的降低了AUV自身導航誤差對定位精度的影響，正交規劃效果最佳，在遠距離長時間定位中有明顯優勢。

為了進一步研究時間同步對兩種方法的影響，在4.1節的參數設置中，加入AUV與靜止目標間的同步誤差20 ms，定位結果見圖10。從圖10(a)和圖10(b)中可以看出，在引入同步誤差后兩種算法的誤差分布趨勢基本相同，但相比于圖7，單AUV定位的定位誤差數值上明顯增大，正交運動AUV誤差影響變化較小。

為了進一步研究AUV航向規劃角度偏差對定位精度的影響，將按照第4節中運動參數和圖6(b)中AUV運動方向，分別設置規劃路徑中每個AUV的偏移航向角從0°～50°，每5°記錄1次定位區域中心位置的均方根誤差。

從圖11中可以看出，當兩個理想正交AUV航向產生10°的偏差情況下，定位精度基本相近，當航向角偏差由10°～30°增加時，該方法的定位誤差略微增大，當航向角偏差大于30°時，該方法的定位效果存在一定程度的降低。

4.2 仿真實驗2 不同通信周期定位誤差實驗

為了研究一個定位周期內不同通信次數定位精度的影響，設計對兩種方法不同通信間隔的實驗，使得每次定位需要2～10次靜止目標與AUV之間的通信。其中，單AUV移動最少需要3次通信完成1次定位，正交移動AUV定位方法最少每個AUV需要2次通信。實驗結果如圖12所示。從實驗中可以看出，對于兩種方法，增加1次定位周期中AUV與靜止目標間的通信次數可以降低定位誤差，但隨著通信次數增多，AUV移動的時間增加，導致AUV自身誤差增大，在該參數實驗下，每個定位周期內靜止目標與每個AUV通信4次定位效果最明顯，超過8次通信則定位精度降低。

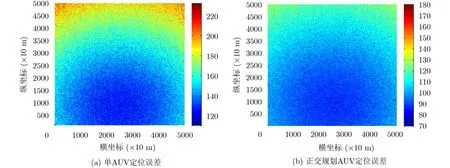
圖10 加入同步誤差后兩種定位方法定位誤差分布圖

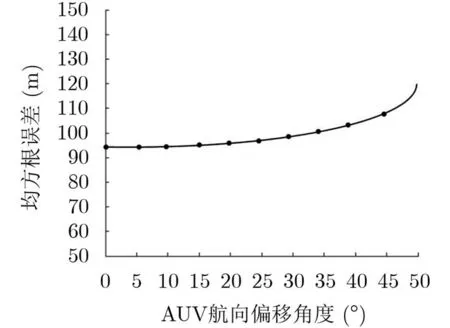
圖11 正交定位誤差與AUV之間航向角誤差關系

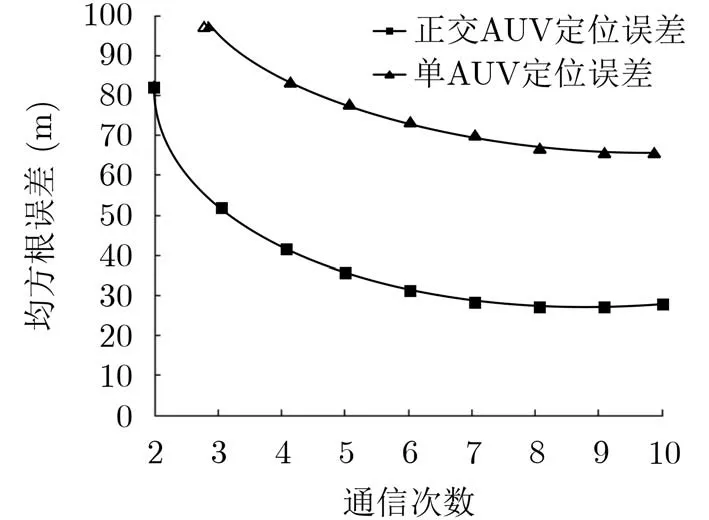
圖12 定位誤差與通信次數關系圖

5 結束語

針對基于單移動AUV的靜止目標定位方法存在定位通信次數多，定位精度低的問題，本文提出了一種正交運動的雙AUV定位方法。該方法利用正交運動的AUV與靜止目標間通信信號時間差，實現測距定位，有效地降低了AUV與靜止目標間的時間同步誤差。同時，本文方法相比于傳統的單AUV定位方法，有效地降低了AUV自身導航系統在長期移動過程中累積誤差對定位結果的影響，同時，本文方法相較于單AUV定位，有效地縮短定位周期，提高了定位精度。實驗結果表明，本文提出的算法在定位精度，有效定位區域覆蓋面積上都有一定程度的提高，為水下大區域靜止目標定位提供可靠方案。但正交運動的雙AUV定位方法，由于需要兩個AUV作為參考節點，與單移動AUV的靜止目標定位方法相比，增加了設備開銷。