用于混合儲能系統平抑功率波動的小波變換方法

程 龍，張方華

（南京航空航天大學 自動化學院，江蘇 南京211106）

0 引言

由鋰電池和超級電容組成的混合儲能系統（HESS）［1-2］彌補了單一儲能系統特性的不足，被廣泛地用于平抑可再生能源發電系統［3］、電動汽車電力系統［4］、多電飛機電力系統［5］的功率波動。鋰電池具有高能量密度，被用于響應幅值低、波動慢的低頻功率分量。超級電容具有高功率密度，被用于響應幅值高、波動快的高頻功率分量。因此，只有根據儲能介質自身的特性，才能更合理地分配波動功率。故本文提出量化儲能介質頻率特性的方法，將其作為負荷功率頻率劃分的參考。在HESS 中，負荷功率分解后的高、低頻分量要與所對應的儲能介質特性相匹配，這樣才能充分發揮儲能介質自身的特性。因此，功率分配方法是平抑功率波動的關鍵因素之一［6］。通常采用濾波的方法將負荷功率根據儲能介質的頻率特性進行高、低頻分解。低通濾波方法因原理簡單、易實現，在能量管理系統中被廣泛應用［7］。但低通濾波器存在相位延遲，容易引起高、低頻功率分量的頻率劃分不清晰，且易造成容量配置冗余度過大等問題［8］。

小波變換能夠實現時域和頻域的相互轉換，同時具有局部化和多分辨率特性，適用于非平穩信號，因此得到廣泛的關注［9-10］。小波變換的關鍵在于小波基和分解層數的優化，優化結果直接影響負荷功率的頻率分配結果。文獻［7］將用于電能質量分析的db4 小波基直接用于風電功率波動的分析，但是兩者在時間尺度、波動幅值、能量等因素上存在較大的差異。文獻［11］通過計算風電功率與小波變換濾波器組的低通濾波器系數之間的互相關系數，選取db6 為最優小波基。在小波變換中濾波系數長度與負荷功率信號的長度存在差異，且計算復雜。小波變換同時存在高、低頻2 組分量，僅用低通濾波器系數無法全面評價所選小波基的濾波器組系數。文獻［12］以收斂性和正則性為依據選取meyer 為最優小波基，但實際上具有這些特性的小波基有很多。文獻［8，12］都是直接給出小波變換的分解層數，并未說明具體原因。文獻［11］根據超級電容的響應頻率確定小波變換的分解層數，但超級電容響應頻率的劃定缺乏客觀理論依據。

為此，本文提出一種基于小波變換的負荷功率頻域分配方法，主要用于解決小波變換中小波基的選取和分解層數的優化這2 個關鍵問題。要求經小波變換后的高、低頻分量與儲能介質的特性更接近，以充分發揮儲能介質的自身優勢。通過算例分析了儲能介質頻率特性與小波變換分解層數的合理性，同時采用HESS 的配置成本驗證互相關系數之和的正確性。

1 儲能介質頻率特性

儲能介質的等效時間TET［5］可表示儲能介質單體的額定功率與所存儲能量之間的關系，見式（1）。

其中，Es為儲能介質單體的額定能量；Pr為儲能介質單體的額定功率。

TET表征了儲能介質單體以額定功率充／放額定能量所需要的時間。在儲能介質單體的一個完整充放電周期內，所需要的時間TT為等效時間的2倍，即TT=2TET。因此，定義儲能介質的響應頻率fT為：

根據儲能介質的相關參數，其響應頻率范圍如圖1 所示。圖中，fTD、fTC分別為等效時間最大、最小時鋰電池單體的響應頻率；fTB、fTA分別為等效時間最大、最小時超級電容單體的響應頻率。由圖1 可見，鋰電池的響應頻率范圍大于超級電容的響應頻率范圍，即鋰電池能夠響應超級電容所能響應的頻率分量。但響應高頻分量會增加鋰電池的充放電次數，縮短其使用壽命［4］。同時，超級電容的最低響應頻率要大于鋰電池的最高響應頻率，超級電容無法響應低頻分量。因此，本文利用鋰電池響應低頻分量，利用超級電容響應高頻分量，這樣可以發揮儲能介質自身特性的優勢。

圖1 儲能介質的響應頻率范圍Fig.1 Response frequency range of energy storage device

2 離散小波變換

2.1 基本原理

小波變換具有多分辨率分析能力，能夠分辨信號中更多的細節信息，適用于非平穩信號。選用小波變換分析負荷功率信息，能夠更好地分解負荷功率中的高、低頻分量。

小波變換通常分為連續小波變換和離散小波變換［13］。連續小波變換中的伸縮、平移相互獨立，小波函數間有一定的相似性，且其計算量大，存在信息冗余，通常用于理論分析。將連續小波變換中的伸縮系數、平移系數進行離散化，可得離散小波變換形式為：

其中，x(t)為待處理信號；j 為伸縮系數；k 為平移系數；ψ(t)為母小波；N為待處理信號的長度。

2.2 小波基的選取

小波基的選取直接影響負荷功率分解后的數據特征。通常選取與待處理信號波形相似的小波基進行小波變換分析［14］，這樣能夠更好地體現待測信號的特征。通常采用互相關系數進行小波基的選取［15］，其計算式為：

其中，ρx，y為互相關系數；x 為待測信號；y 為原始信號；cov(x，y)為2 個信號的協方差；δx、δy分別為信號x、y 的標準差；xi、yi分別為信號x、y 第i 個數據點的值；分別為信號x、y 的平均值；n 為待測信號數據點總數。

信號經小波變換分解后包含高、低頻2 組分量，故負荷功率信號的互相關系數同樣需要考慮高、低頻2 組功率分量。為了能夠同時體現高、低頻功率分量的互相關系數與負荷功率的相關性，本文提出了互相關系數之和的概念，如式（5）所示。互相關系數之和越大，表明小波變換分解后高、低頻功率整體與剩余功率更相似。因互相關系數的最大值為1，所以互相關系數之和的最大值為2。

2.3 分解層數優化

小波變換的分解層數直接影響負荷功率分解后的頻率劃分。對負荷功率進行頻率劃分的主要目的是發揮儲能介質自身的特性。因此，本文基于超級電容的頻率特性提出一種小波變換分解層數優化方法，負荷功率頻率劃分滿足超級電容的頻域特性。

Mallat 快速算法的提出使離散小波變換的應用變得簡單且易實現。Mallat 快速算法主要包括分解、重構兩部分，以3 層小波變換為例，其示意圖見附錄中圖A1。圖A1（a）進行3 層分解，其中，x(n)為待處理信號數據；g(n)為高通濾波器；h(n)為低通濾波器；↓2 表示下2 采樣；D1為第1 層分解的細節部分，位于小波空間；A1為第1 層分解的平滑部分，位于尺度空間。第1 層分解的小波空間、尺度空間將待處理信號的頻域f1+f2+f3+f4進行對半劃分，小波空間為高頻部分f1，尺度空間為低頻部分f2+f3+f4。第2層分解對第1層分解后的尺度空間進行進一步分解，得到細節部分D2和平滑部分A2。第3 層分解對第2 層分解后的尺度空間進行進一步分解，得到細節部分D3和平滑部分A3。3層分解后小波空間中的細節部分為D1+D2+D3，尺度空間中的平滑部分為A3。小波空間、尺度空間滿足直和關系。圖A1（b）進行3 層分解的重構，↑2 表示上2 采樣。將每層的細節部分、平滑部分進行上2 采樣，并進行相應濾波可得到上一層的平滑部分，最終可得到原始信號。

Mallat 快速算法中小波空間、尺度空間的頻率劃分范圍主要由小波變換的分解層數決定。根據香農采樣定理，定義負荷功率的采樣頻率為fs，則負荷功率的頻譜不能超過fs/2。離散小波變換的Mallat快速算法的分解層數與采樣頻率之間的關系見圖2。第1 層分解的尺度空間、小波空間的頻率范圍分別為[0，fs/4]、( fs/4，fs/2]；第2 層分解是對第1 層的尺度空間頻率進行劃分，第2 層的尺度空間、小波空間的頻率范圍分別為[0，fs/8]、( fs/8，fs/4]。每層分解都是對上一層尺度空間的頻率范圍進行平均劃分。

圖2 分解層數與采樣頻率的關系Fig.2 Relationship between decomposition level and sampling frequency

超級電容用于響應負荷功率的高頻分量，根據圖1 可以確定超級電容響應負荷功率高頻分量的最低頻率。因此，以超級電容單體等效時間最大時的響應頻率fTB為基準，與圖2 中小波空間的頻率進行匹配。第l 層分解的小波空間頻率范圍為( fs/2l+1，fs/2l]，實際分配的負荷功率頻率不能小于超級電容的最低響應頻率，即：

3 算例分析

以某一段飛機負荷功率Pload數據為例［5］進行算例仿真分析，具體相關參數見附錄中表A1。發電機響應平均功率Pavg，HESS 響應剩余功率Pre。采用小波變換方法對負荷的剩余功率進行高、低頻功率分配。小波變換的2個關鍵參數的優化流程見圖3，主要包括基于互相關系數的小波基選取和基于儲能介質頻率特性的分解層數優化。

圖3 小波變換關鍵參數的優化流程圖Fig.3 Optimization flowchart of key parameters for wavelet transform

3.1 小波基和分解層數驗證

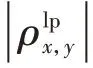
圖4 典型小波基與負荷功率的互相關系數Fig.4 Cross correlation coefficient between typical wavelet base and load power

負荷功率的采樣頻率fs=1 kHz，超級電容的最低響應頻率fTB=0.021 Hz，最高響應頻率fTA=0.045 Hz；鋰電池的最低響應頻率fTD=1.37×10?4Hz，最高響應頻率fTC=6.71×10?4Hz［5］。根據式（6）可計算得到小波變換的分解層數l ≤14.5，故選取最優分解層數為14層。

3.2 仿真分析

3.2.1 頻率特性

根據圖1 所示儲能介質的響應頻率范圍，分析不同分解層數下高、低頻功率分量的頻率特性是否符合儲能介質的頻率特性。為了充分發揮儲能介質的自身優勢，高頻功率分量的頻率主要位于超級電容的最低響應頻率fTB以上，低頻功率的頻率要小于鋰電池的最高響應頻率fTC。

分解層數l為12—16層時小波變換后低頻功率的頻譜見圖5。由圖可見，分解層數越少，低頻功率的高頻分量越多，分解層數為12、13 層時低頻功率中含有較多的高頻分量。此時鋰電池會響應較多的高頻分量，不符合鋰電池的頻率特性。當分解層數越多時，低頻功率分量的頻率特性就越接近鋰電池的頻率特性。進行15、16 層分解時，低頻功率頻率特性更加符合鋰電池的頻率特性，可充分發揮鋰電池的自身優勢。

圖5 不同分解層數的低頻功率頻譜Fig.5 Frequency spectrum of low frequency power with different decomposition levels

分解層數l為12—16層時小波變換后高頻功率的頻譜見圖6。由圖可知，分解層數越多，高頻功率中含有較多的低頻分量，分解層數為15、16 層時分解的高頻功率中含有較多的低頻分量，而頻率小于fTB的分量越多，超級電容則需要響應更多的低頻分量；分解層數為12、13 層時高頻功率中含有少量的低頻分量，高頻功率特性與超級電容的頻率特性更加一致，能夠更好地發揮超級電容的頻率特性。

圖6 不同分解層數的高頻功率頻譜Fig.6 Frequency spectrum of high frequency power with different decomposition levels

對比圖5 和圖6 可知，分解層數為12、13 層時分解的高頻功率中含有少量的低頻分量，但在低頻功率中含有較多的高頻分量，這符合超級電容的頻率特性，卻不符合鋰電池的頻率特性；分解層數為15、16 層時分解的低頻功率中含有較少的高頻分量，但在高頻功率中含有較多的低頻分量，這符合鋰電池的頻率特性，卻不符合超級電容的頻率特性。綜合上述分析，14層分解同時兼顧了高、低頻功率分量與儲能介質的頻率特性，14 層分解的低頻功率與鋰電池頻率特性一致，高頻功率與超級電容頻率特性一致。

3.2.2 互相關系數

3.3 配置成本驗證

表1 HESS的配置結果Table 1 Configuration results of HESS

小波變換分解后高、低頻功率分量的峰值功率和平均能量如表1所示，其結果直接影響儲能介質的配置容量。HESS需同時考慮高、低頻分量所需要儲能介質的配置容量，而容量配置需同時滿足功率約束和能量約束，以確定儲能介質最終配置的容量大小。

對比表1 中不同小波基的小波變換功率和能量可發現，haar 小波基的峰值功率和平均能量均小于dmey 小波基的峰值功率和平均能量。因此，基于haar小波基的配置功率和能量也會小于基于dmey小波基的配置功率和能量。雖然rbio3.1小波基的高頻需求能量最小，但由于需求功率非常大，在進行容量配置時，受功率約束限制，對應的超級電容配置能量也會隨之增加。結合文獻［1］中給出的鋰電池單位能量成本為0.273$／（W·h），超級電容的單位功率成本為0.3$／W，可得表1 所示儲能的配置成本，可見haar小波基下HESS的配置總成本最小，rbio3.1小波基下HESS 的配置總成本最高。上述結果驗證了基于互相關系數之和選取小波基的有效性和正確性。

4 結論

（1）基于儲能介質的等效時間，量化了儲能介質的頻率特性，解決了傳統方法對儲能介質頻率特性主觀判斷不足的問題。

（2）根據Mallat 快速算法，建立了儲能介質頻率與離散小波變換分解層數之間的關系，實現了對儲能介質響應功率頻率的合理劃分。

（3）互相關系數之和同時考慮了小波變換后高頻功率、低頻功率與原始負荷功率的相關性，為負荷功率選取合適的小波基提供了依據；通過比較HESS的配置成本，驗證了基于互相關系數之和選取小波基的正確性。

附錄見本刊網絡版（http：//www.epae.cn）。