解一類(lèi)帶洞非凸域上函數(shù)極值的動(dòng)約束同倫算法

商玉鳳，黨 楊，吳 睿，劉慶懷

(1.長(zhǎng)春財(cái)經(jīng)學(xué)院經(jīng)濟(jì)學(xué)院，吉林 長(zhǎng)春 130122；2.長(zhǎng)春工業(yè)大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，吉林 長(zhǎng)春 130012)

0 引言

考慮如下形式的非凸規(guī)劃問(wèn)題：

minf(x)，
s.t.p(x)≤0，
q(x)≥0.

(1)

其中：f：Rn→R，p：Rn→R，q：Rn→R.易知問(wèn)題(1)的KKT系統(tǒng)為

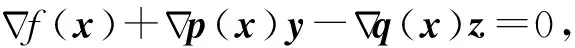
(2)

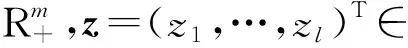
在已有的利用組合同倫方法求解非凸規(guī)劃問(wèn)題中，從幾何上看一般需要滿(mǎn)足法錐、擬法錐、偽錐等條件[1-3]，而帶洞非凸區(qū)域不滿(mǎn)足這些條件.文獻(xiàn)[4]給出了動(dòng)約束組合同倫算法，通過(guò)構(gòu)造動(dòng)約束使其滿(mǎn)足法錐條件，擴(kuò)大了應(yīng)用范圍，但沒(méi)有給出構(gòu)造約束函數(shù)的方法.文獻(xiàn)[5-6]應(yīng)用動(dòng)約束同倫方法討論了不動(dòng)點(diǎn)問(wèn)題以及非光滑非凸規(guī)劃問(wèn)題.本文針對(duì)帶洞非凸區(qū)域上的優(yōu)化問(wèn)題給出了一個(gè)新的同倫方程，利用該方程求解非凸規(guī)劃問(wèn)題可以發(fā)現(xiàn)隨著同倫參數(shù)的變化，約束區(qū)域由一個(gè)有界凸區(qū)域變?yōu)橛薪绶峭箙^(qū)域，由于初始區(qū)域?yàn)橥箙^(qū)域因而不需要驗(yàn)證法錐條件，并證明了路徑的存在性與收斂性，通過(guò)算例表明該方法是有效的.

1 基本假設(shè)

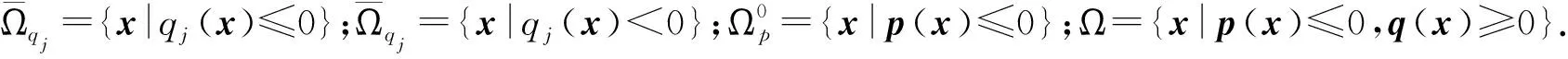
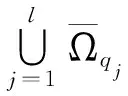
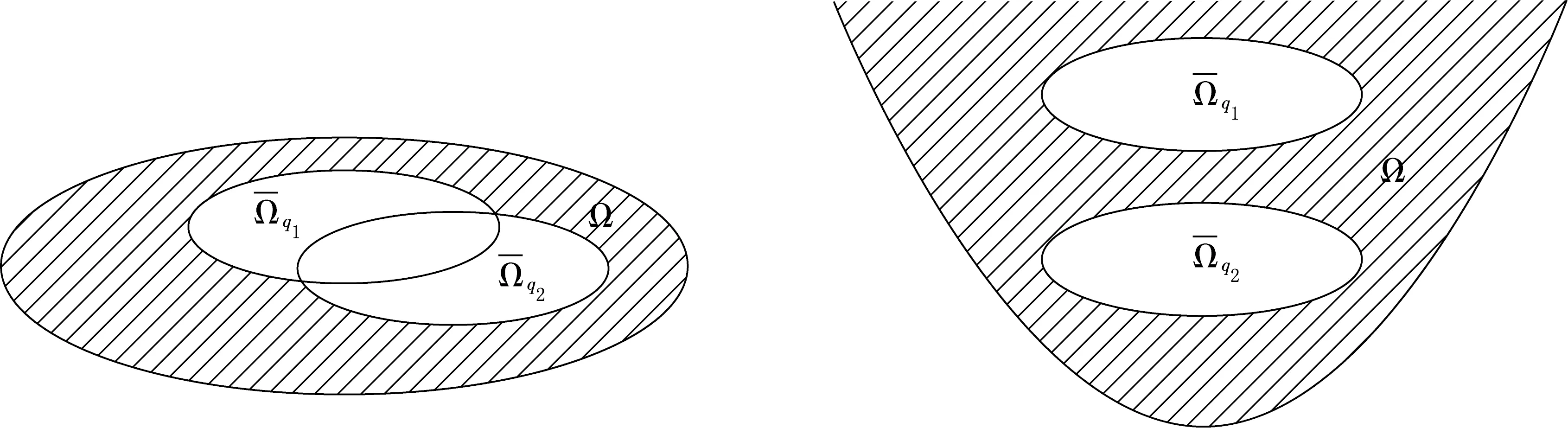
圖1 帶洞非凸區(qū)域示例圖

非空凸區(qū)域與邊界的正獨(dú)立性具有下面性質(zhì)：

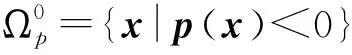
這里Ip(x)={i|pi(x)=0}.

對(duì)給定x(0)∈Rn，t∈[0，1]，定義參數(shù)函數(shù)P(x，x(0)，t)以及Q(x，t)如下：

P(x，x(0)，t)=p(x)-tΘ(p(x(0))+em)，Q(x，t)=tel+(1-t)q(x).

(3)

其中：

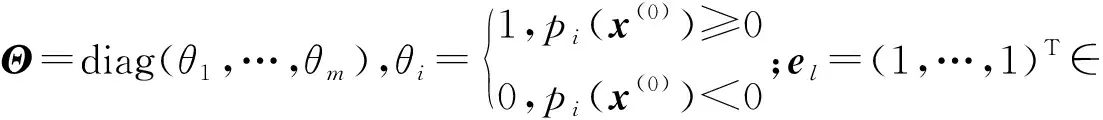
記：

Ω(x(0)，t)={x|P(x，x(0)，t)≤0，Q(x，t)≥0}；

ΩP(x(0)，t)={x|P(x，x(0)，t)≤0}；

ΩQ(t)={x|Q(x，t)≥0}；

?Ω(x(0)，t)=Ω(x(0)，t)Ω0(x(0)，t)；

I(x，x(0)，t)={i|pi(x)-tθi(pi(x(0))+1)=0}；

J(x，t)={j|t+(1-t)qj(x)=0}.

由(3)式P(x，x(0)，t)及Q(x，t)的定義可以得到如下引理：

引理2設(shè)p：Rn→Rn，q：Rn→Rl均為凸向量值函數(shù)，Ω為帶洞非凸域.則當(dāng)t∈[0，1]時(shí)有：

Ω=Ω(x(0)，0)?Ω(x(0)，t)?Ω(x(0)，1)；

ΩP(x(0)，0)?ΩP(x(0)，t)?ΩP(x(0)，1)；

ΩQ(0)?ΩQ(t)?ΩQ(1)；

?ΩP(x(0)，t)∩?ΩQ(t)=?.

考慮含參數(shù)t的優(yōu)化問(wèn)題

minf(x)，
s.t.P(x，x(0)，t)≤0，
Q(x，t)≥0.

(4)

問(wèn)題(4)的KKT系統(tǒng)為

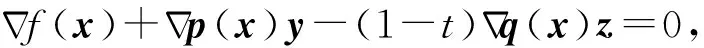
(5)

為求解系統(tǒng)(5)，構(gòu)造組合同倫映射H(x，y，z，t)為

(6)

當(dāng)t=1時(shí)，同倫方程H(x，y，z，1)=0，從而

x-x(0)=0，YP(x，x(0)，1)-Y(0)P(x(0)，x(0)，1)=0，Zel-Z(0)el=0，

此時(shí)方程H(x，y，z，1)=0有唯一的解x=x(0)，Y=Y(0)，Z=Z(0).

當(dāng)t=0時(shí)，同倫方程H(x，y，z，0)=0，即

此時(shí)方程H(x，y，z，0)=0的解即為KKT系統(tǒng)(2)的解.

2 同倫路徑存在性與收斂性

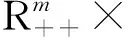
假設(shè)1p∈Cr：Rn→Rm，q∈Cr：Rn→Rl(r>2)均為凸向量值函數(shù).

假設(shè)2Ω={x|p(x)≤0，q(x)≥0}為內(nèi)部非空有界帶洞非凸域.

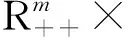
其中En為n維單位矩陣.由Θ的定義，得到

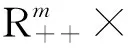
(7)

Y(k)P(x(k)，x(0)，tk)-tkY(0)P(x(0)，x(0)，1)=0；

(8)

Z(k)Q(x(k)，tk)-tkZ(0)el=0.

(9)

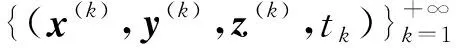
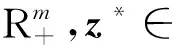
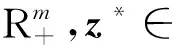
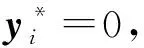
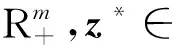
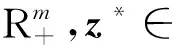
下面證明有且僅有情況(ⅵ)發(fā)生，情況(ⅰ)—(ⅴ)都是不可能發(fā)生的.

(a) 當(dāng)t*=1，k→+∞時(shí)，由方程(9)知，必有‖z(k)‖+∞.若存在則由方程(8)必有i∈I(x*，x(0)，t*).改寫(xiě)(7)式為

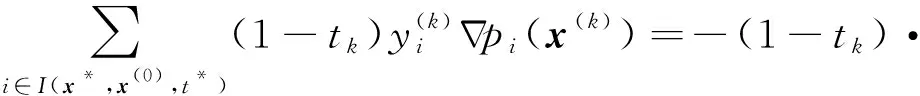
(10)

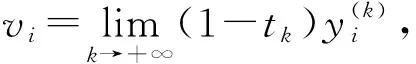
(11)

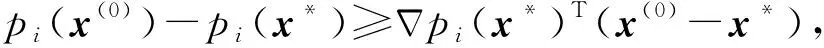
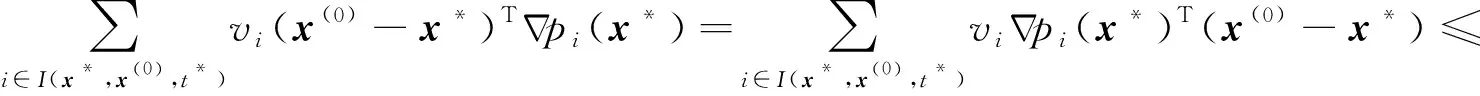
(12)

而對(duì)(11)式右端乘(x(0)-x*)T得到(x(0)-x*)T(x(0)-x*)≥0，這是不可能的，因此‖y*‖+∞，情況(ⅰ)不能發(fā)生.

(13)

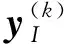
則必有

‖λ‖=1，λ1≥0，i∈I(x*，x(0)，t*)，

由引理1可知所有λi=0(i∈I(x*，x(0),t*)),這是不可能的.

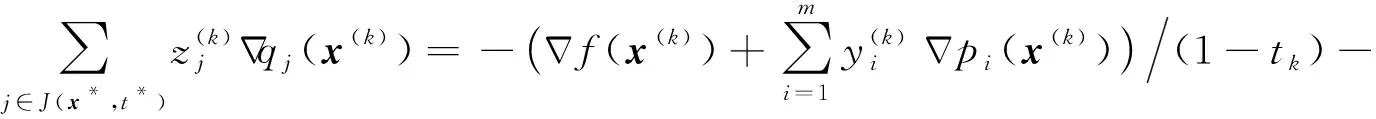
(14)

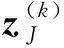
容易看到

‖μ‖=1，μj≥0，j∈J(x*，t*).

由假設(shè)條件3可知μj=0(j∈J(x*，t*))，這與‖μ‖=1矛盾，因此z*必為有限值，情況(ⅱ)不可能發(fā)生.

(c) 由方程(8)和(9)可以看到情況(ⅲ)與(ⅳ)不可能發(fā)生，由0是H(w，t)的正則值，情況(ⅴ)是不可能的.

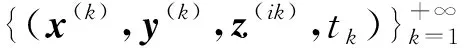
3 數(shù)值算例

本文采用標(biāo)準(zhǔn)的預(yù)估-校正同倫方法跟蹤同倫路徑，編寫(xiě)了Matlab程序.算例中初始點(diǎn)x(0)利用隨機(jī)數(shù)產(chǎn)生，取y(0)=(1，…，1)T，迭代運(yùn)算終止原則為tk<10-12以及‖H(w(0)，w(k)，tk)‖<10-10，具體結(jié)果如下.

例1解R2上非凸優(yōu)化問(wèn)題：

本問(wèn)題的最優(yōu)解為x*=(1.275 3，-1.478 8)T，目標(biāo)值為f(x*)=-17.855 7.利用隨機(jī)函數(shù)產(chǎn)生的4個(gè)初始點(diǎn)分別是x1(0)=(-0.174 1，-1.926 0)T，x2(0)=(1.741 9，1.667 6)T，x3(0)=(-0.219 6，1.713 1)T，x4(0)=(-0.636 0，-0.625 4)T.注意到這里x1(0)?Ω，x2(0)?Ω，x3(0)∈Ω，以及x4(0)?Ω，沿著每一個(gè)初始點(diǎn)都可以到達(dá)最優(yōu)解點(diǎn)x*.圖2給出了當(dāng)t從1變到0時(shí)，初始點(diǎn)x(0)沿同倫曲線(xiàn)Γ變到解點(diǎn)x*的變化路徑.

圖2 例1同倫路徑x1-x2曲線(xiàn)圖

例2解R3上非凸優(yōu)化問(wèn)題：

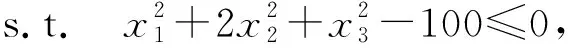
本問(wèn)題有2個(gè)KKT點(diǎn)分別為(x1*，y1*)=(-2.778 2，5.988 4，4.534 4，0.439 8)T，(x2*，y2*)=(-3.166 3，2.603 4，-8.741 8，0.263 3)T；相應(yīng)的函數(shù)值為f(x1*)=-40.522 1，f(x2*)=-11.926 6.利用隨機(jī)函數(shù)產(chǎn)生了4個(gè)初始點(diǎn)，分別為x1(0)=(-0.870 6，-9.629 9，6.428 1)T，x2(0)=(-1.105 9，2.308 6，5.838 7)T，x3(0)=(-8.347 7，6.414 3，-6.139 6)T，x4(0)=(2.280 4，7.826 0，5.241 9)T.注意到x1(0)?Ω，x2(0)∈Ω，x3(0)?Ω，以及x4(0)?Ω.圖3給出了當(dāng)t從1變到0時(shí)，初始點(diǎn)x(0)沿同倫曲線(xiàn)Γ變到解點(diǎn)x*的變化路徑，分別表示t-x1，t-x2，t-x3曲線(xiàn)圖.

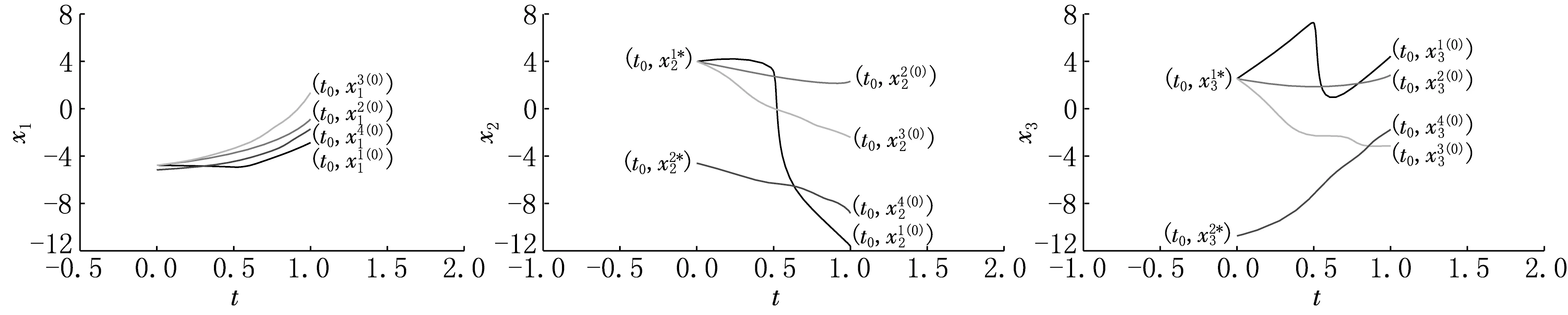
圖3 例2解的路徑t-x1，t-x2，t-x3曲線(xiàn)圖