基于Critic賦權法的隔離礦柱安全厚度優選研究*

龍林健,陳星明,劉傳舉,劉小平,莫 超

(西南科技大學 環境與資源學院，四川 綿陽 621010)

0 引言

隨著資源的開發利用，礦山開采將由淺部向深部轉變；開采深度的增加，將使崩落采礦法所引起的地表沉降范圍大大增加，破壞礦區周邊生態環境，而充填采礦法則可有效控制地表變形。從目前來看，崩落法轉充填法在實際礦山生產中并不少見，但在這兩種采礦方法轉變前需在關鍵分段設置隔離層：一方面可通過設置充填體隔離層，減緩圍巖移動速率，從而保障深部開采礦房的穩定性；另一方面可預留隔離礦柱，由此形成隔離層將兩種采礦方法隔開，從而達到安全過渡的目的[1-2]。

預留隔離礦柱的厚度主要由安全和經濟兩個因素決定，現階段隔離礦柱厚度確定方法主要有理論分析、經驗公式、室內試驗以及數值模擬等[3]。國內常用的隔離礦柱理論計算方法有厚跨比法、荷載傳遞線交匯法、K.B.魯佩涅依特公式法、平板梁法、結構力學法、普氏拱法等[4]。韓進仕等[5]根據隔離礦柱理論，結合數值模擬計算，擬合出了大理石地下開采頂板合理厚度公式。寇向宇等[6]將數值模擬和理論計算相結合，使其研究結果更加真實可靠。裴明松等[7]采用數值模擬方法對程潮鐵礦聯合開采隔離礦柱進行了研究，結果表明，隔離礦柱取20 m時礦山綜合效益最高。曾令義等[8]通過理論計算得出隔離層安全厚度，并結合數值模擬驗證了安全厚度的合理性。現階段利用算法對隔離礦柱厚度進行優選的研究較少，戴興國等[9]基于λ模糊測度和Choquet積分構建了動態綜合評價法，提出了選擇隔離礦柱回采方案的新思路。

本文采用理論公式計算隔離礦柱厚度，利用MIDAS/FLAC3D構建了4種礦體回采數值模型，根據模擬結果選取最大主應力、最小主應力、頂底板位移量作為安全評價指標，以礦石回采率作為經濟評價指標，基于Critic賦權法對4種方案進行優選，以期獲得最優的隔離礦柱厚度。

1 工程背景

某鎳礦二采區采用無底柱分段崩落法開采，該礦地質品位為0.66%，礦體平均傾角約90°，礦體平均厚度為50 m。截至2019年，采區1 590～1 642 m水平礦石回采基本結束。1 642 m水平以上存在厚50 m的第四系表土層、17.3 m的氧化層冒落散體以及32.7 m的氧化層；崩落采礦法出礦量為總回采礦石量的1/3左右，1 590 m水平上部還存在總高度約34.7 m的崩落散體。地層結構如圖1所示。

圖1 地層結構示意圖

崩落法采礦已經使得地表多處出現坍塌，若繼續采用此法開采將會導致地表沉降范圍不斷擴大。為保護礦區周邊環境，保證安全回采，決定將崩落采礦法改為充填采礦法。

2 隔離礦柱厚度計算

為簡化計算，對于隔離礦柱理論厚度的確定，本文選用以下幾種應用較多的數學和力學理論相結合的計算方法。

2.1 厚跨比法

厚跨比法計算式為

(1)

式中：H為隔離礦柱厚度，m；W為采空區跨度，m；K為安全系數。根據礦山設計文件可知，采空區跨度為15 m，安全系數取1.5～2.0。

按厚跨比法計算得到隔離礦柱厚度H≥11.25～15.00 m。

2.2 K.B.魯佩涅依特公式法

K.B.魯佩涅依特公式法計算式為

(2)

式中：ρ為隔離礦柱巖石密度，t/m3；σB為隔離礦柱強度極限，σB=σna/(k0k3)，k0=2～3，k3=7～10，σna=(0.07～0.1)σc，σc為巖石的單軸抗壓強度，MPa；g為隔離礦柱上方散體、氧化礦及第四系表土層對礦柱的壓應力，MPa。

根據礦山巖體力學參數，算得σB=0.44 MPa；g值可結合隔離礦柱上部散體、氧化礦及第四系表土層厚度用公式g=γh計算，算得g=2.825 MPa(γ為礦石容重，h為厚度)。

由K.B.魯佩涅依特公式法算得隔離礦柱厚度為7.1～9.5 m。

2.3 平板梁法

平板梁法隔離礦柱安全厚度計算式為

(3)

式中：γ為隔離礦柱礦巖容重，N/cm3；σt為隔離礦柱巖土體抗拉強度，MPa。

根據礦山巖體力學參數，γ為0.027 N/cm3，隔離礦柱抗拉強度為0.8 MPa。由平板梁法可算得隔離礦柱厚度為5.7～7.6 m。

2.4 結構力學法

結構力學法隔離礦柱安全厚度計算式為

(4)

式中：q為隔離礦柱附加載荷，MPa；b為隔離礦柱單位計算寬度，m；σ許為隔離礦柱允許拉應力，MPa，σ許=σt/K。

由結構力學法算得隔離礦柱厚度為6.9～8.1 m。

綜合上述4種計算方法，算得的安全礦柱厚度分別為11.25～15.00、7.1～9.5、5.7～7.6、6.9～8.1 m。為方便控制變量，故統一取安全系數為2.0時的隔離礦柱厚度作為理論安全厚度。隔離礦柱理論厚度分別取15.0、9.5、7.6、8.1 m。

3 隔離礦柱安全厚度模擬計算

3.1 數值模型構建

該礦山沿用原開拓系統，保持分段高度20 m不變，為減少礦石損失，考慮對第一分段進行部分礦石回采，礦房跨度均為15 m，本次模擬9個礦房回采，采區長度為135 m。對應理論計算結果，隔離礦柱厚度方案為：①方案1，隔離礦柱厚15.0 m；②方案2，隔離礦柱厚9.5 m；③方案3，隔離礦柱厚7.6 m；④方案4，隔離礦柱厚8.1 m。模型長400 m、寬300 m、高255 m，三維網格模型如圖2所示。

圖2 礦體三維網格模型

本次模擬回采分6個時步進行：時步1回采礦房5；時步2充填礦房5，回采礦房3、7；時步3充填礦房3、7，回采礦房1、9；時步4充填礦房1、9，回采礦房4、6；時步5充填礦房4、6，回采礦房2、8；最后充填礦房2、8。礦房布置見圖3。

圖3 礦房布置示意圖

3.2 本構模型及力學參數

模型中的礦巖均為彈塑性材料，因此選用摩爾-庫侖準則作為材料屈服準則。摩爾-庫侖準則表達式為

τn=C+σntanφ，

(5)

式中：τn為滑移面切應力，MPa；C為內聚力，MPa；σn為滑移面上的正應力，MPa；φ為內摩擦角，(°)。

經折減后的巖體力學參數見表1。

表1 巖體力學參數

3.3 模擬結果及分析

本次模擬包括6個回采時步、4種隔離礦柱厚度，因篇幅所限，僅列出各方案回采過程中的最大與最小主應力云圖。

3.3.1 最大主應力對比分析

根據數值模擬結果，最大主應力出現在第4回采時步(見圖4)。

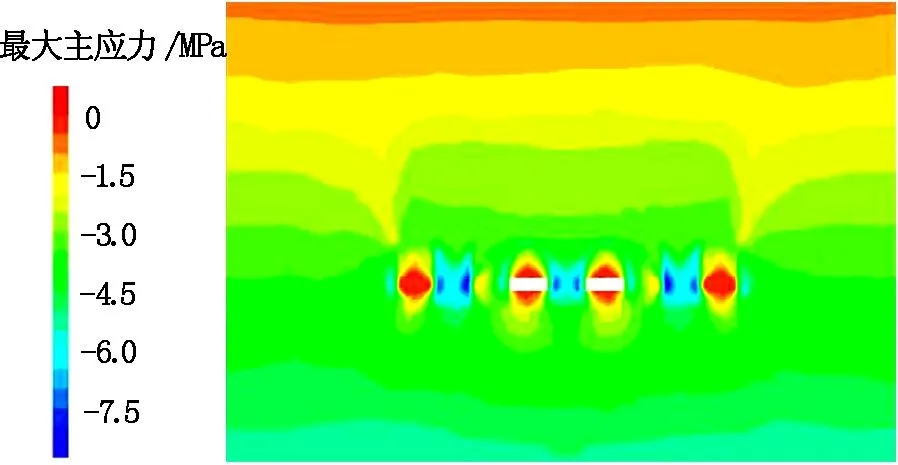
(a)方案1

由圖4可以看出，最大主應力基本出現在礦房兩幫。在礦房開挖過程中，由于應力重新分布，頂底板出現了應力釋放區。對比礦房1、9和礦房4、6的最大主應力云圖可以發現，礦房充填以后并未有效改變其頂底板的應力分布狀態；但從實際生產來看，充填體在采空區內部起到了支撐作用，能有效阻止采空區的進一步變形。模擬結果顯示，4種方案的最大主應力峰值分別為8.292、9.539、7.488、8.243 MPa，即最大主應力峰值排序為方案3<方案4<方案1<方案2。

3.3.2 最小主應力對比分析

各方案的最小主應力云圖如圖5所示。由于在FLAC3D中默認拉應力值為正，壓應力值為負，因此根據最小主應力云圖可以確定最大拉應力值的大小。由圖5可知，在礦房回采過程中，最大拉應力出現在礦房頂板處，根據現場情況，頂板一般是受拉破壞，表明數值模擬結果與實際相符。4種方案的最大拉應力值分別為0.591、0.592、0.583、0.600 MPa，均未超過礦石抗拉強度0.730 MPa。最小主應力峰值排序為方案3<方案1<方案2<方案4。

(a)方案1

3.3.3 位移量峰值

因篇幅所限，位移云圖不在此一一列出。位移量變化情況如圖6所示。

(a)頂板沉降峰值折線圖

由圖6(a)可知：當隔離礦柱厚度為15.0 m時，頂板沉降量僅為1.192 cm；而當隔離礦柱厚度減小至9.5 m時，頂板沉降量達到了7.436 cm；隔離礦柱厚度下降至7.6 m和8.1 m時，沉降量均有增大。由此看出，頂板沉降量隨著隔離礦柱厚度的減小呈現逐漸增大的趨勢。4種方案的頂板沉降峰值分別為1.192、7.436、12.360、10.680 cm，即頂板沉降峰值排序為方案1<方案2<方案4<方案3。

由圖6(b)可知，各方案底板鼓起峰值較為接近。4種方案的底板鼓起峰值分別為0.722、0.719、0.743、0.739 cm，即底板鼓起峰值排序為方案2<方案1<方案4<方案3。

綜上可知，各方案均存在其優勢指標，如最大主應力與最小主應力峰值均為方案3優于其他方案，而位移峰值則是方案1和方案2優于其他方案。如根據數值模擬結果主觀判斷最優方案可能會使最終結果出現偏差，故本文采用Critic客觀賦權方法，以回采率為經濟指標對隔離礦柱厚度進行優選，以期獲得隔離礦柱最優厚度。

4 基于Critic賦權法的隔離礦柱厚度優選

4.1 Critic賦權法簡介

Critic方法是由DIAKOULAKI提出的一種客觀權重賦值法，該方法主要適用于多屬性、多目標的決策，其主要思路是基于決策矩陣信息，建立數學模型計算權值[10]。Critic客觀賦權法綜合模型構建步驟如下。

4.1.1 數據預處理

為消除量綱的影響，各指標應使用以下兩個公式之一進行歸一化處理：

(6)

(7)

式中，max(xij)和min(xij)分別為某一指標在該類指標中的最大值和最小值，xij為第i種隔離礦柱厚度的第j個評價指標。其中式(6)適用于效益型指標歸一化，式(7)則適用于成本型指標歸一化。以歸一化后的數據建立評價矩陣M′。

4.1.2 計算評價指標變異性及沖突性系數

標準差σj是評價指標變異性的表征量，在此假設Critic客觀賦值法評價矩陣M為一個m×n的矩陣，評價指標的沖突性系數計算式為

(8)

4.1.3 計算權重系數

各評價指標的客觀權重確定是以指標內的變異性和沖突性來綜合表征的，其計算式為

(9)

根據評價指標的權重系數，可獲得權重矩陣W=[w1w2…wn]。

4.1.4 建立綜合評價模型

結合上述構建的歸一化評價矩陣M′與權重矩陣W的轉置矩陣相乘，即可獲得綜合評價模型ST，其表達式為

ST=M′×WT，

(10)

式中，WT為權重矩陣W的轉置矩陣。

4.2 方案優選

在模擬結果的基礎上，以礦石回采率為經濟指標進行評價，以獲得隔離礦柱最優厚度。各方案評價指標見表2。

表2 各方案評價指標

根據表2，利用式(6)、式(7)對其進行歸一化處理，得到歸一化評價矩陣

結合Critic賦權法，根據評價矩陣求出各指標標準差即變異系數σj(見表3)，計算評價指標的相關系數(見表4)，根據相關系數計算指標沖突性系數(見表5)，結合式(9)計算各指標權重系數(見表6)，最后將評價矩陣與權重系數相乘得到各方案的最終得分(見表7)。

表3 評價指標變異系數

表4 評價指標相關系數

表5 評價指標沖突性系數

表6 評價指標權重系數

表7 各方案最終評分

從表7可以看出，方案1、方案2、方案3評分結果較為接近，其中方案1評分最高，即最優的隔離礦柱厚度為15.0 m。

5 結論

a.通過厚跨比法、K.B.魯佩涅依特法、平板梁法以及結構力學法對某鎳礦崩落法轉充填法過渡階段隔離礦柱厚度進行了理論計算，得到隔離礦柱在安全系數為2.0時的理論厚度分別為15.0、9.5、7.6、8.1 m。

b.經數值模擬計算，得到了4種不同隔離礦柱厚度下的最大主應力峰值、最小主應力峰值、頂板沉降峰值、底板鼓起峰值。

c.以最大主應力、最小主應力、頂板沉降、底板鼓起和回采率5個參數作為評價指標，采用Critic賦權法構建評價模型，對隔離礦柱厚度進行優選，最終得出最優隔離礦柱厚度為15.0 m。