把握課堂追問時機 提升初中生數學思維品質

王金水

（集美區后溪中學，福建 廈門 361024）

數學是關于思維的科學，數學課堂教學離不開提問，有效提問又離不開追問.通過步步追問，步步精心，問出質量，問出智慧，以此激活學生思維，激發學生積極思維，提升學生思維高度.然而，當前課堂教學卻存在這樣的現象：追問等待時間過短，無法給予學生啟迪思維和想象的時空；追問內容缺乏生成性，有預設沒生成；追問的問題過泛，導致追問沒有抓住問題的核心；追問時機不及時，難于誘發學生進一步思考.

追問是教師對某一問題，在一問之后再提問，又再提問…是對初次提問的補充、深入、拓展或修正的一種教學行為.追問，在于探路，探索思維方向；在于激疑，激發質疑思維；在于辨析，辨別反思能力；在于明理，提升思維水平；在于延伸，構建知識網絡［1］.追問是教學的生命，追問是師生往來互動、共同發展的過程.恰到好處的追問可以促進學生深入思考，激活學生思維，從而拓寬思維的廣度，增進思維的深度，鍛造思維的強度.行是知之路，學非問不明.如何在學生思維盲點處進行的追問，將問題引出沖突，引出思考，是一個亟待解決的問題.

筆者以為追問要做到適時而問，難易恰當，富有啟發，切中要害，尤其是在混淆處、矛盾處、“經驗”處、意外處的追問，問出方法，問出根源、本質，不僅能使課堂錦上添花，化平淡為神奇，還能快速提升學生的思維品質.

一、追問于混淆之處——悟化

追問在于辨析，培養學生辨別領悟的能力.對于一些易混淆的概念，學生思維易困惑的地方，把握好追問的時機很重要.此時此處的追問，能引發學生的深思，幫助學生解除疑慮和消除模糊，促使學生豁然開朗.

例1 若關于x的方程無解，求m的值.

生1：無解相當于方程有增根，故分母為0，易得增根為x=1.通過去分母，得x+1=-mx-1.當x=1時，m=-3.

巡視發現普遍學生都是這樣做，顯然他們混淆增根與方程無解的概念.

追問1：無解相當于方程有增根嗎？

追問旨在正視存在的問題，在于激疑，激發學生質疑的思維，消除疑惑，形成解決問題的策略.事實上，追問引發學生從不同角度各抒己見，但觀點分散，論據不足，無法突破要害，得從方程無解概念入手，這顯然需要最簡方程.

師：解方程最終都要回歸到什么方程？

生眾：最簡方程ax=b.

追問2：最簡方程ax=b，何時會出現無解？

圍繞核心問題展開有效思考，旨在幫助學生轉換問題思考角度，回歸到原始概念上，化解抽象，減少學習思維負荷，打開思路.

生2：a=0 且b≠0.

追問3：當a=0 且b≠0，最簡方程ax=b無解，能說它有增根嗎？

追問目的是理清學生疑慮和困惑，及時走出誤區，糾正認識偏差.通過此追問，學生自然明白無解與增根不是一回事，即增根是方程有根，只是這個根會讓原方程失去意義.

生3：本題解法應該是x+1=-mx-1，有x+mx=-2，得(1+m)x=-2，當m=-1 時，x的系數為0，方程無解.

生反問：如果m≠-1 時，方程一定有解嗎？

學生的反問為引入增根做了鋪墊.其他學生自然認為有解，方程的解為

追問4：此時x值是任意實數嗎？

追問目的是逐步提高學生發現問題的能力.此追問很有針對性、啟發性.

生4：還有x≠1.因為x=1，此時分母為0.

生5：對，x=1 是增根，應舍去.要排除增根對應的m的值，由，當x=1 時，有m=-3.所以，本題m的值可以為-1，也可以為-3.

追問5：方程無解與方程有增根有什么關系？

此時學生可自主歸納：增根是造成方程無解一種因素，無解是無法找到方程左右兩邊相等的未知數的值.

變式：若關于x的方程有增根，求m的值.

變式強化了學生對方程無解與方程有增根的理解.追問堪比追蹤，不在于問題多少，而是找到關鍵之處，讓人有一種意猶未盡的感覺，并在充分思考中有所感悟，在感悟中有所獲得，這樣學生的思維才有廣度與深度，課堂才有厚度.

二、追問于矛盾之處——催化

學生常會對某個問題出現相左的見解，應抓住時機，展開追問，催化學生數學思維.追問不僅啟迪學生思維，找出錯誤產生的原因，幫助學生糾正錯誤，激發學生的求知欲.追問也能理清思路，問出本質，化解矛盾，并通過創造性回答，實現創新意識的培養.

例2 已知直線y=mx-x+m是一次函數，求m的取值范圍.

旨在讓學生理解掌握一次函數一般形式及其概念.學生化解析式為y=(m-1)x+m，由一次函數概念，易得m≠1.

師：若直線y=(m-1)x+m的圖像經過點A(2，4)，m為何值？

知識性問題，旨在讓學生掌握一次函數對應點與線間的關系.

追問1：直線y=(m-1)x+m的圖像能不能經過點B(-1，4)？

理解性問題，幫助學生轉換問題思考角度.

生1：不能，把B(-1，4)代入y=(m-1)x+m，發現等式不成立.

生2：m是變量，意味著直線可以平移或旋轉，根據線動成面，點B 也是平面內一點，按理說這些變化的線所構成的面會覆蓋B 點.

學生從代數與幾何方面切入，卻得出對立的結論.怎么會這樣？這是一種求助信號.教會質疑，引起思考，引發反“追問”，才有可能解惑.

追問2：不論m為何值，直線y=(m-1)x+m的圖像能垂直x軸嗎？

追尋學生思維軌跡，釋放潛能，調動學生的主動性、積極性和創造性.

生3：當m=1 時，直線平行x軸，當m≠1 時，直線是一次函數，不能垂直x軸.

追問3：從圖形上看，不論m怎樣變化，直線y=(m-1)x+m有何特點？

筆者引導學生任取m 的值，在各自導學案上對應的直角坐標系作圖.再任取部分同學的畫法，重疊，投影，展示.學生猛然發現這些線都會過點（-1，1）.然后再引導學生認真觀察解析式y=(m-1)x+m.

追問4：從解析式上看，能不能把y=(m-1)x+m看成y是m的函數？

生4：可以，轉化成y=(x+1)m-x.

引導學生自主發現，對于y=(x+1)m-x，此時，當x=-1 時，y恒為1.通過數與形結合讓學生明白，不論m怎樣變化，直線y=(m-1)x+m繞定點（-1，1）旋轉，但直線永遠不會與x軸垂直，當然就不能過B點了.

追問5：直線y，經過A(2，4)，B(3，b)，C(4，c),如何比較b，c 大小？

從幾何代數等多角度追問，旨在讓學生提出不同見解，在交流辨析中形成共識：由圖像經過定點（-1，1）與A(2，4)，可確定直線走向，此時y的值隨著x的值增大而增大.易得b＜c.追問中也培養了學生勇于放棄或修正自己的觀點，催化了學生把思維引向廣處，拓展學生的邏輯思維，達到對知識的深度解讀，實現了思維課堂的本質.

三、追問于“經驗”之處——點化

由于許多學生受思維定式的影響，通過追問消除定勢，點化思維，開啟智慧，積累基本經驗，提高解決現實問題的能力.

例3 甲乙兩店在一次促銷活動中，甲店推出4.5折優惠，乙店則買100 送120 購物券.

師：若你去購物，你會選擇哪一店？

旨在積淀數學活動經驗.通過引發學生激烈的爭論，關注學生之間經驗的差異.

生1：買100 送120 購物券，那商家不是虧本？

生2：打4.5 折太少了，應該選擇買100 送120 購物券.

生3：買100 元得120 元購物券.相當于花100 元，賺20 元，不買豈不是虧了？

…

營造真實的交流氛圍，促進思維展開.發現學生全憑經驗，出現這種現象，不是缺少必備的知識，而是缺少實踐智慧，掩蓋了他們對生活現象的洞察力.

追問1：什么情況下才能得到120 元購物券？

似懂非懂時實施追問，才能使學生產生頓悟，才能把學生的思維引向關鍵處，讓知識由模糊走向清晰.

生4：乙店要購買100 元或以上，而購買100 元以下就沒有了.

生5：乙店有沒有優惠，得看你購物多少.

由于在甲店有購買就有優惠，學生明白了買100元以內的要選甲店.有學生反問道：100 元以上怎么辦？從被追問走向主動追問，培養學生愛思考、會追問的學習品質.

追問2：按乙店方案：假設你買了120 元的商品，超過了100 元，超過部分不足100，只得120 元券（又用來購物），相當于你用120 元現金得到240 元商品，是這樣嗎？

用特例揭示事實真相，讓學生對知識的理解由片面走向全面.

生眾：是的，100 元以上200 以內，只得120 元的購物券.

追問3：現在的折扣率是多少？

生6：折扣率是120÷240=0.5，只打5 折.超過100部分沒有折扣，顯然更不合算.

不妨乘勢而上、趁熱打鐵，再追一問.

追問4：如果購買的商品價格剛好100 元？

生7：折扣率是100÷220＞0.45.

在連續的追問、問中有問的情況下，啟發了學生的發散思維，使學生真正明白了乙店不管買多少都不比甲店便宜.

通過適時地追問，讓前一問的具體內容和思維角度成為下一問的“原點”.我們要做的就是尋著學生的思維軌跡，緊追不舍，由此及彼、由淺入深地追問，從而實現思路就越追越清，問題就越追越明，知識就越追越多.

四、追問于意外之處——激化

通過捕捉課堂意外，激化思維創意，循序漸進地將思維引向深處，從而促進知識的引申與生成，感受到獲得新知的成就感.

例4 如圖1，等腰梯形ABCD，AD∥BC，AB=DC，∠ABC=45°，∠BOC=120°，求的值.

圖1

把學生的思維引向開闊地帶，激活思維，培養問題意識和求知欲望.

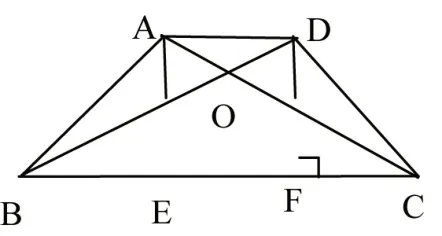
圖2

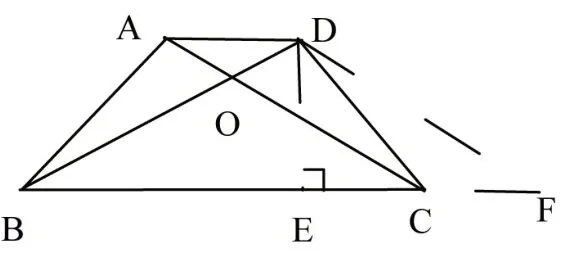
圖3

生3：在圖4 中，若延長BA、CD 交于點E，所以∠E=90°.因為AD∥BC，△EAD∽△EBC，所以

生3 的解法令人驚喜，也令人意外.此時，學生思緒飛揚，tan 15°值是多少？一石激起千層浪，大家情緒高漲，躍躍欲試，讓學生主動追問是追問的最高境界.

師：探究tan15°的值.

旨在引導學生思維的方向，喚起學生強烈探求欲望，引導學生觀察圖4 的結構，啟發30°，45°，60°這些特殊值與15°之間的關系，為學生提供架構性支持.

順勢一擊，抓住一點，將學生的思維引向遠方.

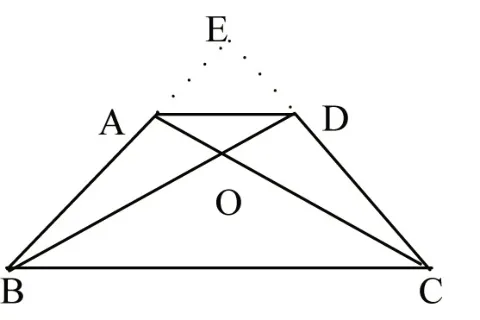
圖4

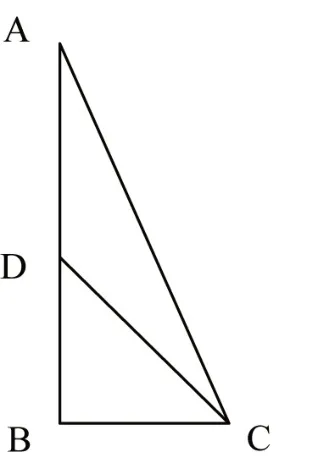
圖5

師：還可以用兩幅三角板拼出15°的角，如圖6 到圖8 等［2］，均求出tan 15°的值.有興趣的同學課后再做深入研究.

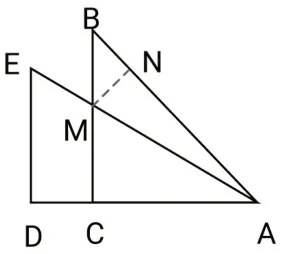
圖6

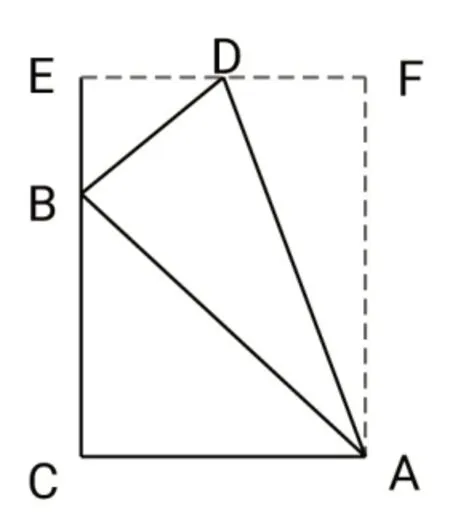
圖7

圖8

追問追求的是一種“激活效應”，讓學生產生對預授知識的向往，為高中學習三角函數埋下伏筆.通過追問感受到了學生思維的激流涌動，讓學生有突發奇想的機會，讓“節外生枝”演繹出獨特的價值，從而起到了“一石激起千層浪”的效果.

課堂教學應抓住稍縱即逝的契機，以之為生長點，巧妙地引發學生思考，激發每一個思維的增長點，從而驅動思維不斷生長.靈活、自然地實施課堂追問，尤其是在混淆處、矛盾處、“經驗”處、意外處的追問，可以起到畫龍點睛、迷途知返、余音繞梁、撥云見日之功效.我們要做的是把握好追問的時機，在追問中統籌兼顧數學知識、思想方法，引發學生與教師思維火花的碰撞，將思維引向深處，從而提升思維品質，實現教學相長.