基于簡易裝置的空氣柱共鳴的聲速測量實驗

翦知漸，周艷明，謝 中

(湖南大學 物理與微電子科學學院 大學物理實驗中心，湖南 長沙 410082)

“互聯網+”時代大學物理實驗課程的教學模式有了很多變化和發展[1，2].目前各大MOOC平臺上有很多高校都開設了大學物理實驗課程，作為線下課程的一種有益補充發揮了很好的作用[3-5].同時，線下課程的教學也大量融入了線上教學的元素，虛實結合的教學模式已成為物理實驗教學的新方向[6，7].一直以來，大學物理實驗的MOOC課程的實驗操作部分主要是以虛擬仿真實驗為載體，而虛實結合教學模式的實驗操作部分基本上是在實驗室環境中完成的，所以要在學生動手能力培養等方面滿足課程教學大綱的要求仍舊離不開實驗室的基礎環境.如何使實驗課程的遠程教育發展得更均衡、更有效力，是物理實驗教學的從業者們需要思考的問題，而今年的新冠疫情使得全世界的實驗課程教師都直接面對了這一問題，很多人都給出了各自的解決方案——“宅+實驗”[8]，這些教學方案在實際教學過程中發揮了巨大的作用，也取得了很好的效果.

湖南大學物理實驗中心設計了一系列的居家實驗項目，再加上虛擬仿真實驗，基本可以替代實驗室環境下的實驗教學.這些實驗方案的設計基于居家環境下隨手可得的實驗器材，不以精確測量為主要目的，側重于對學生實驗方案設計能力、動手能力、數據處理能力的訓練.因為實驗條件的限制，實驗結果可能誤差較大，但通過分析實驗的物理過程，控制實驗條件或改進實驗方案，都可以有效提高實驗結果的精度，這個過程對于培養學生的實驗素養是很有益處的.

本文討論其中的一個項目“空氣柱振動的頻率特性”，并對實驗過程中的一些影響因素進行分析，消除系統誤差后，聲速的測量結果在誤差范圍內與標準值符合.

1 實驗原理與實驗方案

1.1 實驗原理

本實驗的研究對象是空氣柱振動發聲時的共鳴現象.聲波在一頂端開口、底端封閉的均勻圓柱形容器中傳播時會在底部被反射，容器中的聲場實際上為入射波與反射波的疊加，如圖1(a)所示，聲源頻率合適時，將形成穩定的駐波.瓶底反射處是剛性反射面，因而形成波節.如果瓶口處正好是波節，則該處空氣的振幅基本為零，對向外發出的聲音沒有貢獻，此時聽到的聲音就會比較小；如果瓶口處是波腹，則對外發出的聲音將會增強出現共鳴的現象，波幅增加一倍，聲強增加到四倍.所以，如果聲源是多頻率混合的，容器會有“選頻”的作用，符合共振條件的音頻將會被放大.

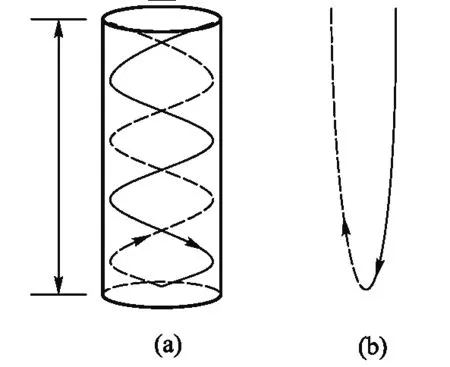
圖1 管狀容器中聲波的共振

因為相鄰的波節與波腹的間距是λ/4，所以能產生共振的最長的波長是4L，如圖1(b)所示的半個駐波；每當波長滿足L=λ/4 +nλ/2(n為任意非負整數)時，都將會產生共振.因此，最長波長4L對應的頻率f(f=c/4L，c為空氣中的聲速)稱為基頻，相應的3f、5f、7f……是泛音頻率.空氣柱對外傳播的聲音是一個復音，基頻決定了空氣柱發聲的音調，泛音決定了它的音色.

當向容器中注水時，聲源實際上是水流撞擊水面發出的聲音，這個聲音里面包含的頻率非常豐富.頻率不符合共振條件的聲音，將很難傳出容器，而頻率符合共振條件的聲音將會被放大，所以聽到的聲音基本上只有符合共振條件的音頻.注水的過程中，空氣柱的長度將會逐漸縮短，也就是共振的波長越來越短，所以聽到的聲音其音調越來越高.

設空氣柱的長度為L=L0-βt，這里L0是測量開始時空氣柱的長度，β是均勻注水時瓶中水面上升的速度.因此聽到的聲音頻率(基頻)將會是

(1)

由實驗測出注水過程中聲音頻率的變化，對實驗數據進行適當處理后，聲音頻率的變化應該能滿足式(1)，并可由此求得聲速值.

1.2 實驗器材與實驗步驟

準備一細長、均勻的圓柱形透明容器(細長的瓶子或水杯)；米尺；膠帶；一部下載了Phyphox APP軟件的智能手機(圖2).在接近容器底部的位置做一水平標志并測量其到頂端的距離L0(主要是防止容器內的底部不夠平整)，打開水龍頭往容器中勻速注水，控制流速使得容器注滿水的時間至少為30秒(但要保持水流連續).然后用手機秒表功能測量水面高度從底部標志線增漲至瓶口時所需的時間t0，則可得β=L0/t0.

圖2 實驗所用器材：細長容器、米尺、膠帶、智能手機

保持水的流速不變，清空容器，準備開始實驗.打開手機App Phyphox的“Frequency history”功能模塊，水面高度到達底部標志線時開始測量，Phyphox將會記錄每個時刻接收到的聲音頻率，數據還會以圖形的方式實時顯示在屏上.數據記錄界面如圖3所示.水面快接近瓶口時停止測量，在菜單欄中選擇“Export Data”導出數據.

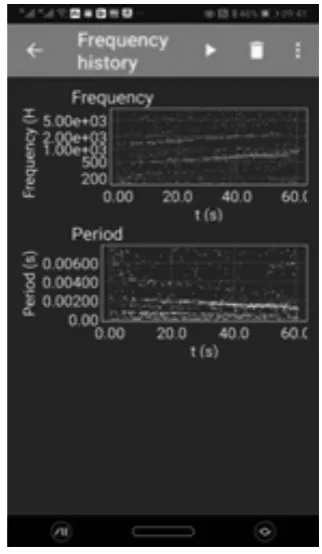
圖3 Phyphox的數據記錄界面

2 數據處理

首先觀察數據記錄的圖形，如圖4所示.“Frequency history”功能模塊的采樣周期是0.04545s，采樣頻率約22Hz，使用不同的容器、不同水流速度進行的實驗，其記錄的數據分布會有較大差別.為什么會出現這種情況？

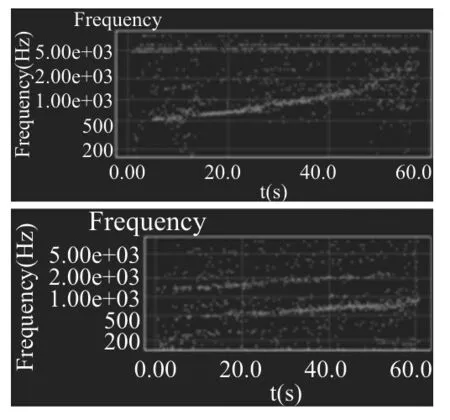
圖4 兩次不同的實驗，記錄數據顯示的圖形

因為APP是先對接收到的聲音信號作頻譜分析，在采樣的那個時刻，APP所記錄的頻率是該時刻聲音頻譜中強度最大的頻率分量.因為水流速度不同、容器材質不同、周圍環境不同等都會使得聲音的頻譜不一樣，因而各時刻采集到的聲音頻率就會不一樣，其中會包含基頻f的聲音、泛音3f甚至5f的聲音，還有環境噪音.因為水流較小聲音低沉，而且高頻聲音易于衰減，所以數據記錄中基頻的數據點最多.可以看到，基頻帶是位于數據圖下方的那條較粗的數據帶，其他的則是噪音和泛音的數據點.

將數據導入Origin并作出頻率值的散點圖，圖5是某次測量的數據.因為數據記錄中基頻的數據點最多，形成了帶狀，所以對數據的處理主要是針對基頻帶的數據進行分析，因此要將基頻帶之外的數據點排除，利用Origin的“屏蔽數據點”功能即可做到這一點.對屏蔽處理后的數據點進行非線性擬合，結果如圖6所示.

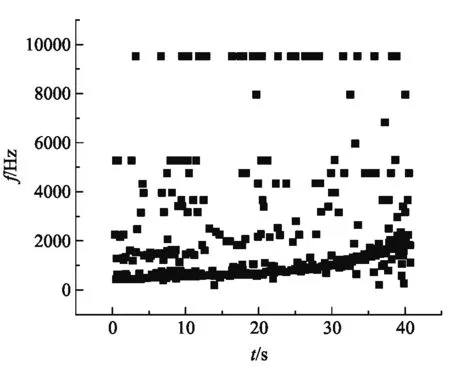
圖5 頻率記錄值的原始數據散點圖

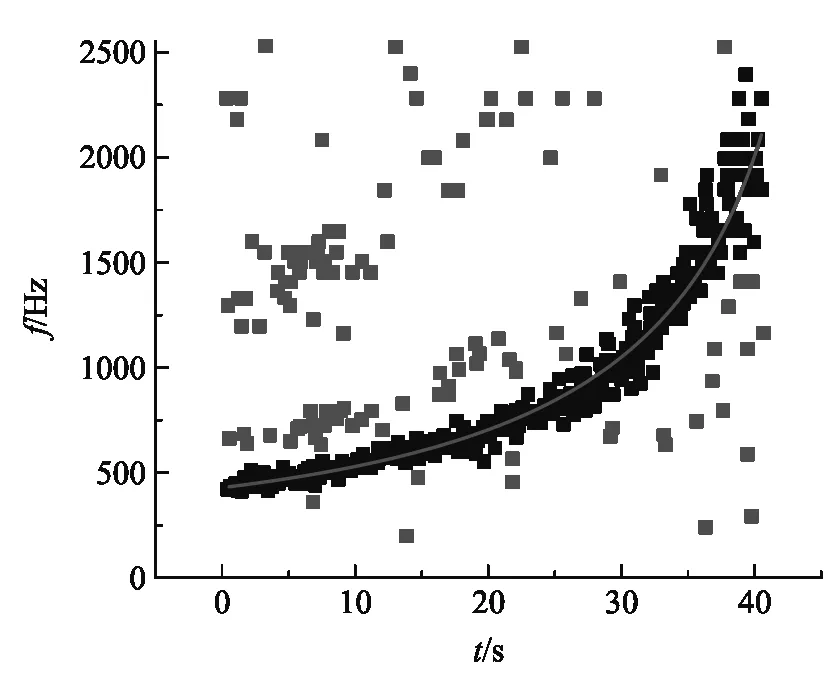
圖6 基頻帶數據點.紅色的數據點是被屏蔽的非基頻點，紅色曲線是對基頻帶的非線性擬合結果

根據頻率隨時間的變化關系式(1)，非線性擬合所采用的函數表達式為

(2)

比較式(1)和式(2)，可以得到對應關系：a? 4L0/c，b?-4β/c.

圖6中的數據其擬合結果為：參數a=0.00234，b=-4.588×10-5，COD=0.95974.可以看到，對于非線性擬合而言，擬合曲線與實驗數據符合得還是相當不錯的.

聲速的計算：因為是基頻帶，故聲波波長為λ(t) = 4(L0-βt)，所以我們得到聲速為

(3)

將測得的初始參數L0和β代入，可得到時刻ti的波長λ(ti)，從擬合曲線中可得到時刻ti的頻率擬合值f(ti)，因此有

(4)

N為有效數據點的個數.圖6的這組數據中，L0= 0.178 m，β=0.003765 m/s，利用式(4)計算可以得到c= 303.5 m/s.

作為比較，測量時室溫下的標準聲速值約為338.9 m/s.從結果中可以看出，測量值與標準值有較大偏差.

3 對測量結果的分析和修正

利用空氣柱共鳴演示共振現象，并用于測量聲速的實驗多見于報道[9-11]，但相關研究基本上只給出了實驗方法，并未對結果進行分析.一般來說，測得的聲速與標準值比較其偏差基本在容許范圍之內.

本實驗方案所得結果與標準值相差頗大(10.5%)，已超出了正常范圍.雖然簡陋的測量條件會帶來較大的誤差，但這里長度的測量誤差小于2%，時間的測量誤差在2%左右，即便再考慮其他因素帶來的誤差，測量結果的偏離也不應該有如此之大，一定存在某種系統誤差.

3.1 L0的修正值

在本實驗中，因為管長較短，聲波傳輸的阻抗特性帶來的影響不能忽略，由此產生的誤差必須考慮.設管長為L，管半徑為r，聲波波數為k，管底(x= 0)為聲源，其阻抗為Z0；管口處(x=L)阻抗為ZL，有如下關系[12]：

(5)

其中S為管橫截面積(πr2)，ρ0、c分別為空氣密度與空氣中的聲速.

因為管口是開放的，存在聲輻射，所以其阻抗為輻射阻抗[12]：

ZL=ρ0cS(R1(2kr)+jX1(2kr))，

R1(x)=1-2J1(x)，

X1(x)=2H1(x)/x

(6)

其中J1為一階Bessel函數，H1為一階Struve函數.當頻率較低時(kr<<1)，上式簡化為

(7)

實際上只要kr<0.5上式即可成立.

空氣柱共振的條件是Z0為一個純粹的聲阻(虛部為零)，將式(7)代入式(5)，在kr<<1的條件下可得共振條件為

tan(nπ-kL)=(8/3π)kr≈tan(8kr/3π)

(8)

ΔL=8r/3π ≈ 0.85r

(9)

稱為末端修正或管口修正，這個現象相應地也稱為管口效應.

圖6的實驗數據中，所用容器的管口直徑為0.048 m，因此ΔL= 0.0204 m，ΔL/L0超過了11%，可見末端修正帶來的影響很大.

實際上末端修正可以很容易用實驗證明：將實驗用的容器清空，放入一個連接了可調節頻率的音頻發生器的小手機耳機(如使用手機App如Frequency Sound Generator作為音頻發生器).開始時容器內的耳機聲音很小，實驗者很難聽到，當改變頻率至最低共振頻率時，實驗者即可聽到明顯的共鳴聲.從測得的最低共振頻率可以計算出波長，從而得到空氣柱的長度.實驗結果證實，末端修正基本是正確的.

見于文獻報道的其他類型空氣柱共鳴的實驗中，因為空氣柱較長而管直徑較小，而且測量的往往是高于基頻的共振頻率，因此管口修正帶來的影響較小，一般都忽略或歸入了測量誤差.本實驗是在簡陋環境下進行的，一般使用的都是短而粗的容器，所以管口修正帶來的影響就不能忽略.

3.2 β值對結果的影響

β是一個測量值，其意義為管中水面上升的速度，看起來似乎與管口效應無關，但從前面的分析中可知基頻的波長表達式為4(L0-βt)，所以β真實的意義是“空氣柱長度”縮短的速度，而空氣柱的長短是與末端修正有關的.

實際上，在3.1中計算管末端的阻抗ZL時，是在低頻近似下(kr<0.5)得到表達式(7)的，當頻率逐漸升高的時候這一點并不能總是被滿足.如圖7所示[12]，當頻率較高時管末端阻抗ZL的實部R1增加得很快，虛部X1也不再近似滿足與kr的線性關系，隨著kr的增加X1是一個逐漸減小的振蕩.因此高頻時管口效應帶來的影響是很復雜的，固定不變的末端修正公式(9)不再適用.因此空氣柱長度的變化不僅與β有關，也與末端修正值隨時間(頻率)增加而引起的變化有關，這實際上也就意味著β不再是一個常數，而與時間有關.

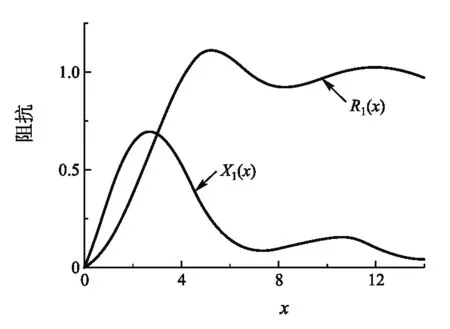
圖7 輻射阻抗的實部和虛部隨x變化的關系曲線.R1為實部，X1為虛部，其中x = kr

另一方面，β作為測量值是一個常數，在公式中也是一個常數參量.聲速計算公式(3)是時間的非線性函數，計算結果對β的變化非常敏感.如圖8所示，如果輸入不同的β值，聲速的計算結果隨時間的變化趨勢可能完全相反.圖8中兩條曲線顯示的是在測量水面上升速度β時，水面升至瓶口的時間僅僅相差±0.9 s的結果，這樣的誤差在手動測量時間的時候很容易產生.

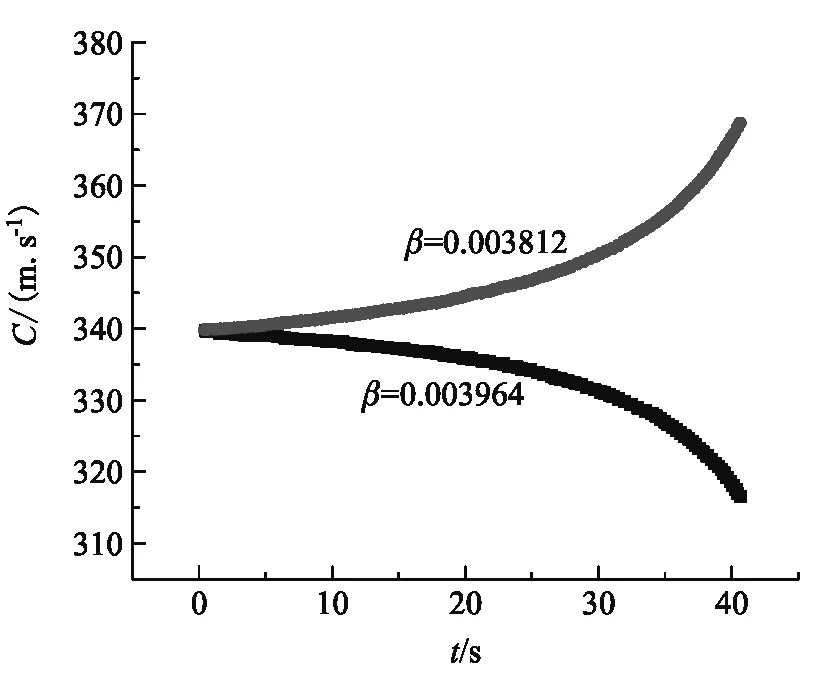
圖8 β值的微小變化給聲速計算值帶來的影響.灰色點是β取值偏小的結果，黑色點是β取值偏大的結果

所以為了減小β的測量誤差帶來的影響，再考慮到這種影響隨時間非線性增加的因素，在計算聲速的時候應該截斷時間較大的數據(也就是高頻部分).怎樣確定時間的截斷點？從前面的分析來看，末端修正式(10)成立的條件是kr< 0.5，或者說是λ>4πr，對于基頻來說就是4(L0-βt) > 4πr，因此要求：

(10)

將β和修正后的L0代入式(4)，應用式(10)截斷高頻部分的數據點，即可計算出聲速測量的實驗結果.

3.3 實驗結果及其討論

為了驗證本實驗方法的有效性，本文選擇了一些不同的容器進行實驗，它們的區別主要是長度和直徑的比值不同.所得結果如表1所示.

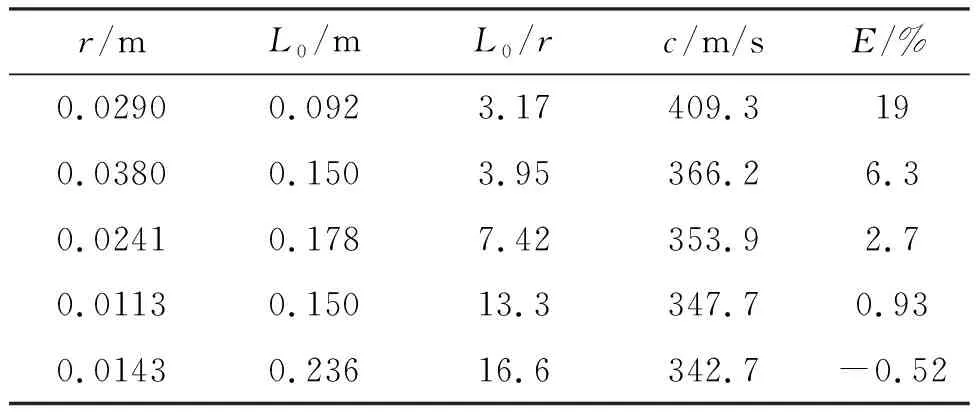
表1 不同長度與口徑的圓形容器測得的聲速

表1中r為容器內半徑，L0為初始長度，L0/r為長度/半徑比，c為按前述方法測量并計算所得的聲速，E為與標準聲速的偏差(實驗時標準聲速為344.5 m/s).從表中數據可以看出，細長容器所得結果更為準確，而且比值L0/r越大結果越好.當長度/半徑比小于4的時候，誤差較大，用這種方法來測量聲速已不適用.

實際上，當長度/半徑比很小的時候，容器已經不能看作是“管”了，而應該看做是一個“聲容”，前述的討論將不再適用.

4 結論

基于簡易測量裝置進行的空氣柱共鳴實驗，易于操作，但在物理原理的學習與理解方面還是很有價值的.在實驗過程和數據處理過程中，學生能夠在數學建模、數據發掘與提取等方面得到很好的訓練，同時對如何改善實驗環境、消除引起誤差的因素等方面得到實際的鍛煉，提高了實際動手解決問題的能力.

因為實驗條件的限制，本實驗研究的空氣柱是在短而粗的容器中進行的，這就產生了一些新的問題.本文經過分析發現，在計算聲速時需要考慮管口的聲輻射導致的管口效應，應該給管長加上一個修正值，同時還需截斷頻率較高的數據點，這樣才能得到正確的聲速測量結果.作為基本聲學知識的延伸，本實驗方案提供的數據處理方法可以使學生在多方面得到訓練和提高.