球狀物體作微形變時彈性勢能的研究

于鳳軍, 湯振杰，田俊龍，張希威

(安陽師范學院 物理與電氣工程學院，河南 安陽 455000)

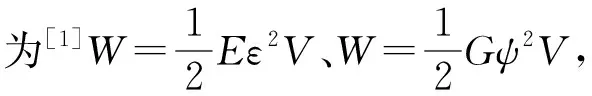
1 一般情況下的彈性勢能密度

一般情況下, 應變和應力都用張量[2]描述, 在直角坐標系Oxyz中, 設應變張量的各分量為exx,exy,exz,eyx=exy,eyy,eyz,ezx=exz,ezy=eyz,ezz; 應力張量的各分量為:σxx,σxy,σxz,σyx=σxy,σyy,σyz,σzx=σxz,σzy=σyz,σzz. 由文獻[2]式(12.5-3)可知, 當應變張量的各分量改變δeij(i,j=x,y,z)時，應變能密度w的增量為

δw=σxxδexx+σyyδeyy+σzzδezz+

2σxyδexy+2σyzδeyz+2σzxδezx

(1)

文獻[2]式(12.6-7)給出各向同性的均勻彈性體的胡克定律：

(2)

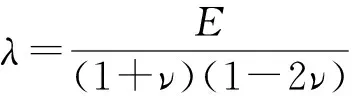
(3)

由于本文所研究的系統不可壓縮, 即無體積膨脹, 故上式中的相對體膨脹為

θ′=exx+eyy+ezz=0

(4)

對于球體, 取球坐標系(r,θ,φ)更方便, 應變張量的分量為err,erθ,erφ,eθr=erθ,eθθ,eθφ,eφr=erφ,eφθ=eθφ,eφφ.考慮式(4), 將式(3)變換到球坐標系, 得彈性勢能密度

(5)

當應變張量eij(i,j=r,θ,φ)已知時，通過上式在球內進行積分，就可得到彈性勢能.

2 彈性球的形變描述

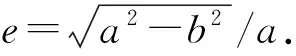
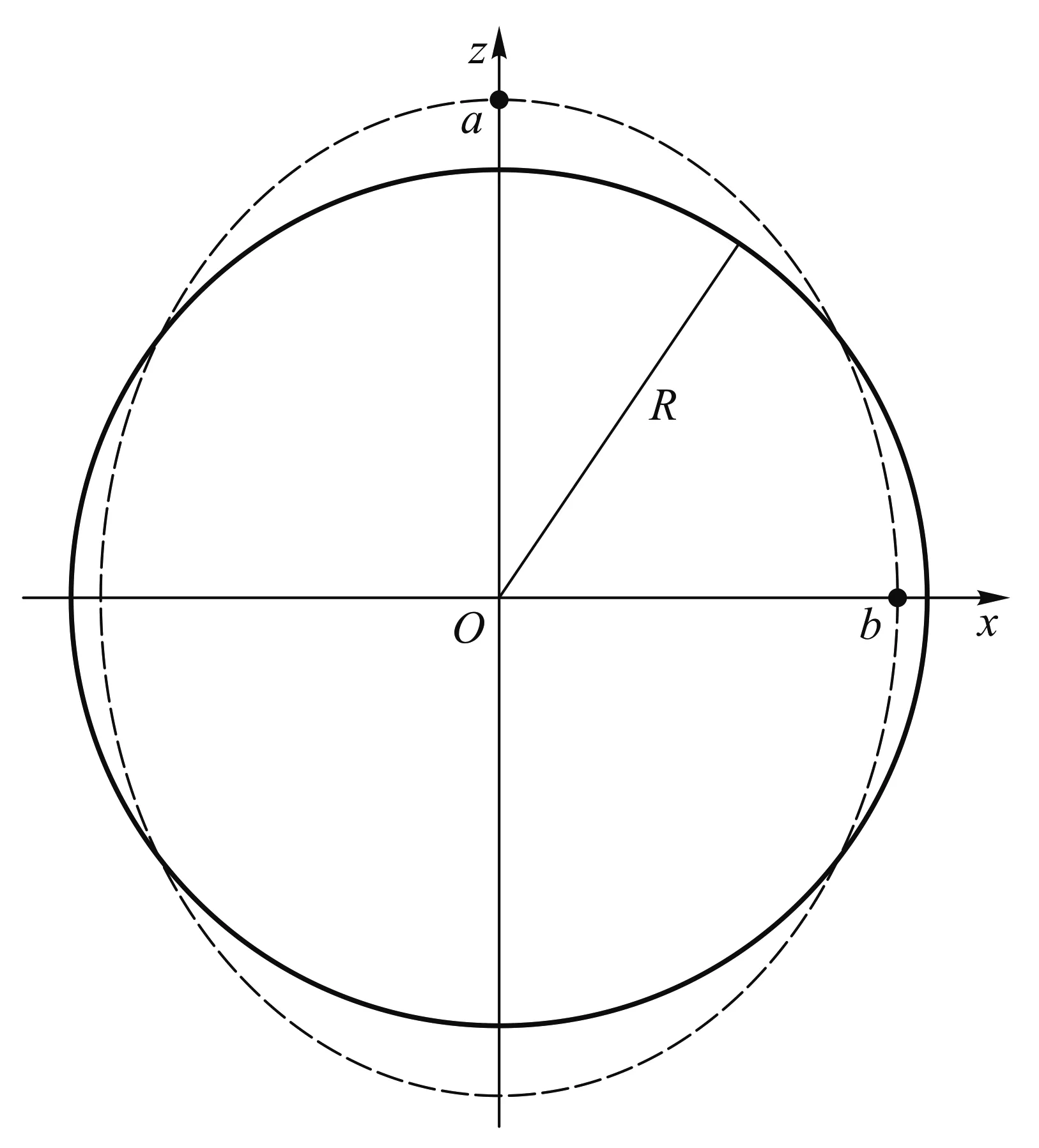
圖1 彈性球形變為長旋轉橢球

(x2+y2)/b2+z2/a2=1

(6)

將x=rsinθcosφ,y=rsinθsinφ,z=rcosθ代入上式得

(7)

由于e<<1，將上式展開, 僅保e的最低次項

(8)

上式是橢球表面在球坐標系中的方程, 其中P2(cosθ)是勒讓德函數.

當彈性球表面形變為橢球表面時, 其體內每一點將離開原來的位置產生微小位移. 設點(r,θ,φ)處質點的位移為

S(r,θ,φ)=Srer+Sθeθ+Sφeφ

(9)

其中,er,eθ,eφ分別是徑向、經線切向、緯線切向的單位向量,Sr、Sθ、Sφ分別是位移沿er,eθ,eφ方向的分量，它們都是點的坐標(r,θ,φ)的函數. 根據文獻[3]式(13.5.14)知, 應變張量分量與位移分量的關系為

(10)

式(8)、式(9)、式(10)構成對彈性球形變的描述. 如果知道位移分量Sr、Sθ、Sφ的具體函數式, 則通過式(10)可以確定應變張量，再由式(5)和體積分計算, 求彈性勢能.

3 位移分量Sr、Sθ、Sφ函數式的確定

由于彈性球沿z方向拉長為長旋轉橢球, z方向處于er、eθ構成的平面內, 故體內各質點的位移可能有er、eθ方向的分量, 不可能有eφ方向的分量, 即Sφ=0. 因為橢球具有繞z軸的旋轉對稱性, 所以Sr、Sθ與φ無關, 僅是r、θ的函數,故設Sr=u(r)f(θ),Sθ=v(r)g(θ),其中u(r)、f(θ)、v(r)、g(θ)是待定函數. 綜上所述, 位移分量可表示為

(11)

本問題的邊界條件是: 球面上各質點的徑向位移使球面變成由式(8)決定的橢球面, 各點的切應力和切應變為0, 即erθ|r=R=0. 此外, 還受到不可壓縮條件(4)的約束, 并且位移為有限值. 下邊利用這些條件求待定函數.

根據式(8), 球面上質點的徑向位移條件、即邊界條件為

(12)

令式(11)第一式中r=R, 并與式(12)對比，得

(13)

f(θ)=P2(cosθ)

(14)

故Sr=u(r)P2(cosθ). 將此表達式和Sθ=v(r)g(θ)代入式(10)第四式運算，將得到erθ的表達式(注:下邊所有復雜的公式推導皆由Mathematica軟件完成)，然后再利用邊界條件erθ|r=R=0，得

(15)

由上式可得,g(θ)=Kcosθsinθ, 其中

(16)

為常數. 將式(14)、上述g(θ)代入式(11)得

(17)

在球坐標系中, 不可壓縮條件(4)可變換作:

err+eθθ+eφφ=0

(18)

把式(17)分別代入式(10)的前三式后, 一并代入式(18)化簡, 有如下結果:

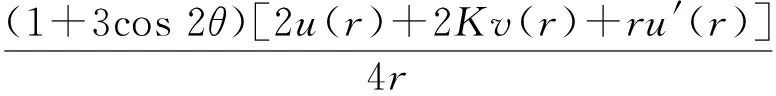
(19)

由于上式中因子(1+3cos 2θ)不恒等于0, 故有2u(r)+2Kv(r)+ru′(r)=0, 即

(20)

根據上式和式(17), 位移分量表示為

(21)

至此, 位移分量函數式(21)中僅剩一個待定函數u(r).u(r)的一個邊值條件為式(13), 另一邊值條件可由式(20)先確定出v(R)、v′(R)，再代入式(16)得到

R2u″(R)+2Ru′(R)+4u(R)=0

(22)

下面由最小勢能原理確定u(r)滿足的微分方程. 將式(21)代入式(10), 式(10)再代入式(5), 并在整個球內積分, 可得彈性勢能:

26r2u′2+32ruu′+32u2]dr

(23)

顯然,W的大小與u的函數形式有關. 根據最小勢能原理, 當一個力學系統平衡時, 勢能取最小值. 因此，現在的問題是上式中當u取何種函數形式時能使W最小,W的最小值是什么. 這是一個泛函的極值問題[4]. 令

26r2u′2+32ruu′+32u2

(24)

將上式代入歐拉方程[4]:

(25)

可得u(r)滿足的方程:

r4u″″2+8r3u′″-24ru′+24u=0

(26)

上式是歐拉型常微分方程, 對其有現成的解法[5], 其特征方程為

γ(γ-1)(γ-2)(γ-3)+8γ(γ-1)(γ-2)-

24γ+24=0

(27)

這是一個一元4次方程, 容易驗證，γ的4個根為: -4,-2,+1,+3. 故u(r)的通解為

u(r)=Ar-4+Br-2+Cr+1+Dr+3

(28)

其中,A、B、C、D是待定常數. 當r=0時u(r)有限, 所以A=B=0. 據此, 將式(28)分別代入邊值條件(13)、(22)，得二元一次方程組:

(29)

解得:C=8e2/15,D=-e2/(5R3). 故由式(28)得

(30)

把上式代入式(21), 可得位移分量函數式的最終結果

(31)

4 彈性勢能的計算結果

將式(30)代入式(23)運算, 可得彈性勢能

(32)

其中,V=4πR3/3為球體積.

5 討論

1) 與直桿的彈性勢能對比. 式(32)表明, 當彈性球形變為長旋轉橢球時, 其彈性勢能與變形參數——橢球偏心率e的4次方成正比, 與彈性模量和體積成正比. 我們將這一結果與直桿的彈性勢能作個對比. 令式(8)中θ=0, 可得彈性球在z方向的半徑相對變化:(r-R)/R=e2/3, 這也是直徑沿z方向的相對變化Δd/d=e2/3, 即e2=3Δd/d. 另外, 切變模量與楊氏模量關系為μ=G=E/(1+ν)/2. 將上二式代入式(32)

(33)

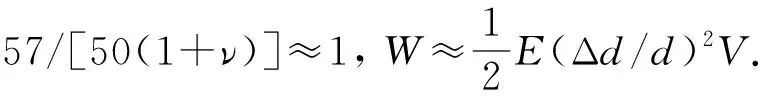
2) 彈性勢能分布.將式(31)代入式(10), 式(10)再代入式(5), 可得勢能密度與點坐標(r,θ,φ)的關系:

24r2(7r2-8R)cos 2θ+9r4cos 4θ]

(34)

根據上式能夠了解勢能密度沿徑向的變化情況. 如圖2，設原點的勢能密度為wo，以比值r/R為橫軸，以比值w/wo為縱軸， 分別作出θ沿0°、45°、90° 3個方向上w/wo隨r/R的變化曲線. 圖中3條曲線自下而上分別對應0°、45°、90°. 顯然, 橢球中心的勢能密度最大.大體上講, 距中心越遠, 勢能密度越小.這一特點也可以通過“等勢能密度線”圖看出. 圖3給出了通過z軸的任一剖面內的“等勢能密度線”圖,圖中亮度與w成正比. 可以看出, 中心的亮度最高,w最大；偏離中心越遠, 亮度越低，w越小.等密度線近似是橢圓, 其長軸垂直于z軸, 這意味著“等勢能密度面”近似為繞z軸的扁旋轉橢球面.

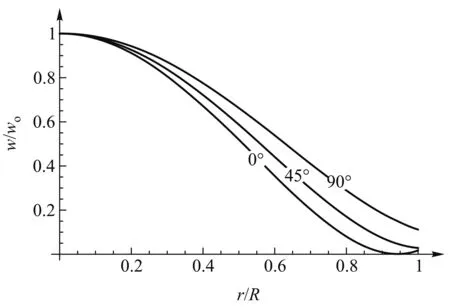
圖2 勢能密度隨徑向的相對變化

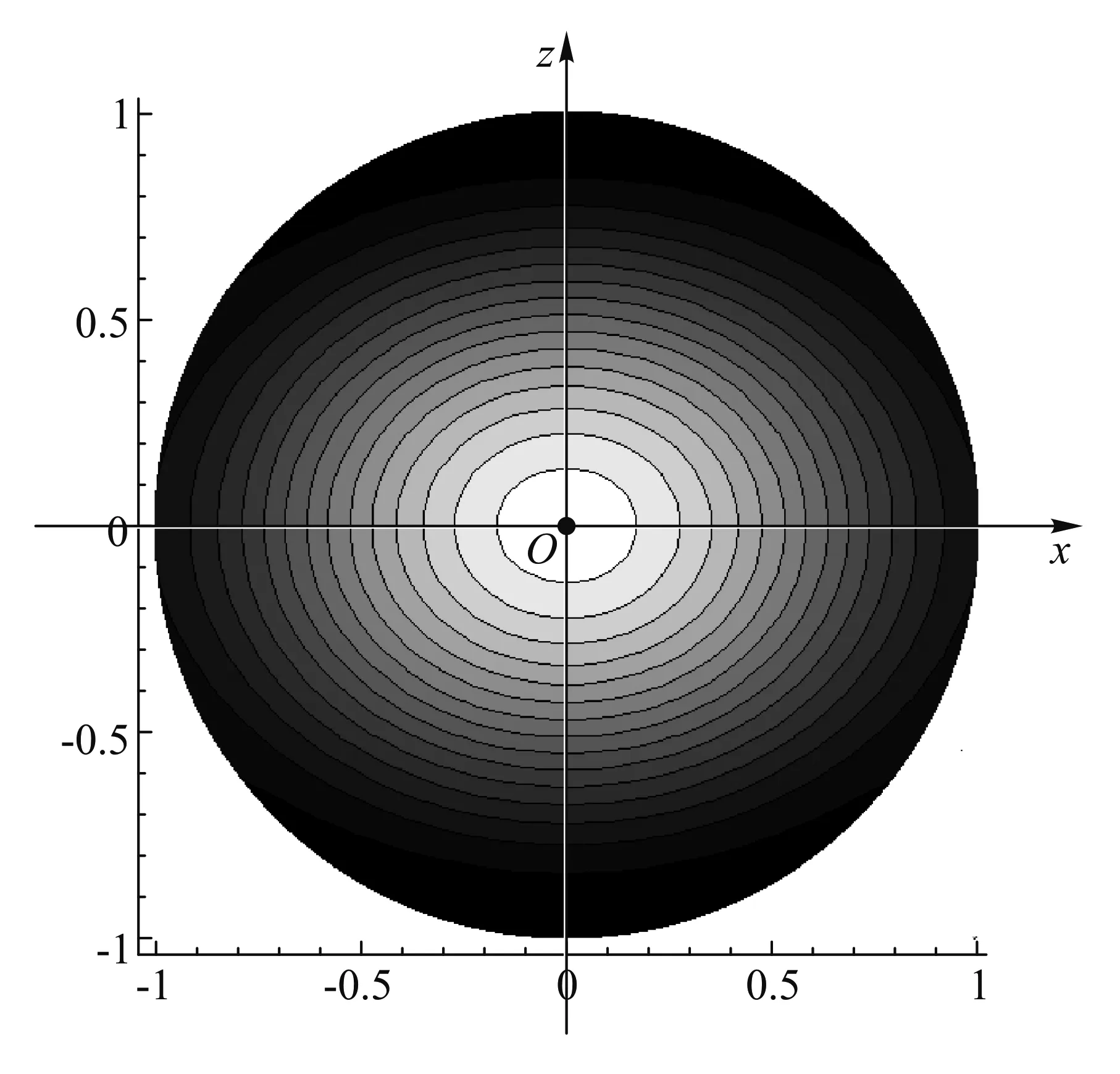
圖3 等勢能密度線

結語：以上求出一個彈性球形變為長旋轉橢球時的彈性勢能或應變能. 首先, 通過應變能密度增量公式和胡克定律，導出應變能密度與應變張量的關系式(3)，利用標準橢球方程導出彈性球在保持體積不變的前提下形變的幾何描述式(8)；然后，通過一個原理、六個條件確定出位移函數式(31), 它們分別是最小勢能原理、橢球沿z方向拉長條件、繞z軸的旋轉對稱條件、球面上各質點的徑向位移條件、球面上各點的切應力切應變為0條件、不可壓縮條件、位移有限條件. 最后通過彈性勢能密度與應變張量的關系、應變張量與位移分量的關系和體積分，得到本文想要的結果，并且進行了有益的討論. 本文以闡述物理定律、物理原理和物理條件的如何應用為主線，對于數學部分，由于運算工作量很大，對求偏微分、多重積分、化簡等，都使用Mathematica軟件完成. 因此，本文不僅能作為彈性勢能方面的教學案例，也可作為學生學習Mathematica軟件的實踐素材.