球對稱靜電場求解方法

呂 嫣, 崔 崧, 李慧玲

(沈陽師范大學 物理科學與技術學院, 沈陽 110034)

0 引 言

靜電場是一種特殊形態的物質,它與實物物質的區別在于看不見也摸不著。為了確定靜電場的分布,引入電場強度這個物理量,所以求解靜電場就是給出空間電場強度的分布[1-7]。求解靜電場是“電磁學”和“電動力學”2門課程所研究的重要問題[8-9]。在電磁學里,通常是用高斯定理來求解具有對稱性的電場分布,而分離變量法[10-13]是電動力學中常用的求解靜電場方法。除此以外,電場強度定義法、電場疊加法、等效法、電勢疊加法,基于唯一性定理的試探法、鏡像法、格林函數法等都可以用來求解不同情況的靜電場。初學者往往分不清這些方法的適用條件,對于給定問題不能正確合理地選擇相應的方法來進行計算,也不熟悉各種方法的解題步驟。基于這種情況,需要對靜電場求解問題做一梳理。雖然不同的方法有不同的適用條件和解題步驟,但同一問題有時也可以用不同方法進行求解,這樣做的好處是可以比較各種方法的特點和適用性。比如考慮半徑分別為R1和R2的2個同心球面,均勻帶電,各自帶有電荷Q1和Q2。下面用不同的方法來求解空間電場分布,并加以比較。

1 由場源分布確定電場分布

根據場源電荷的分布可以由電場疊加原理直接求解靜電場,因為上述問題具有球對稱性也可以由靜電場的高斯定理求解。

1.1 電場疊加法

先考慮一個均勻帶電為Q的球面。如圖1所示,取環形面元dS=2π(Rsinθ)Rdθ,dq=σdS,σ=Q/4πR2。環形面上各點到場點P的距離都相等,在P點產生的電場為

圖1 帶電球面的電場Fig.1 Electric field of a charged sphere

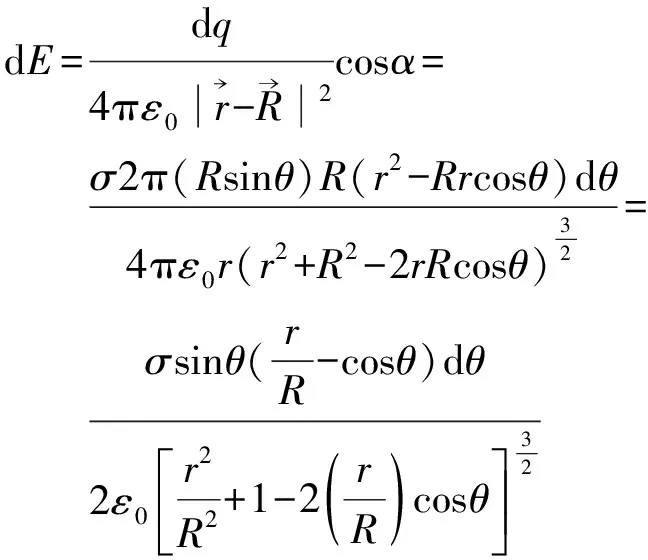
(1)

整個帶電球面在場點產生的電場為

(2)

積分可得

(3)

再考慮2個同心球面產生電場的疊加性可得

(4)

原則上可以由電場疊加原理求任何電場分布問題,無論場源電荷分布均勻與否,帶電體形狀規則與否,它都是適用的,但如果場源電荷分布不均勻,帶電體形狀不規則,則求解是十分困難的,有時甚至是不可能的。

1.2 高斯定理法

由于電荷分布具有對稱性,相應的電場分布也具有對稱性,所以該問題還可以由高斯定理求解。高斯定理的數學表達式為

(5)

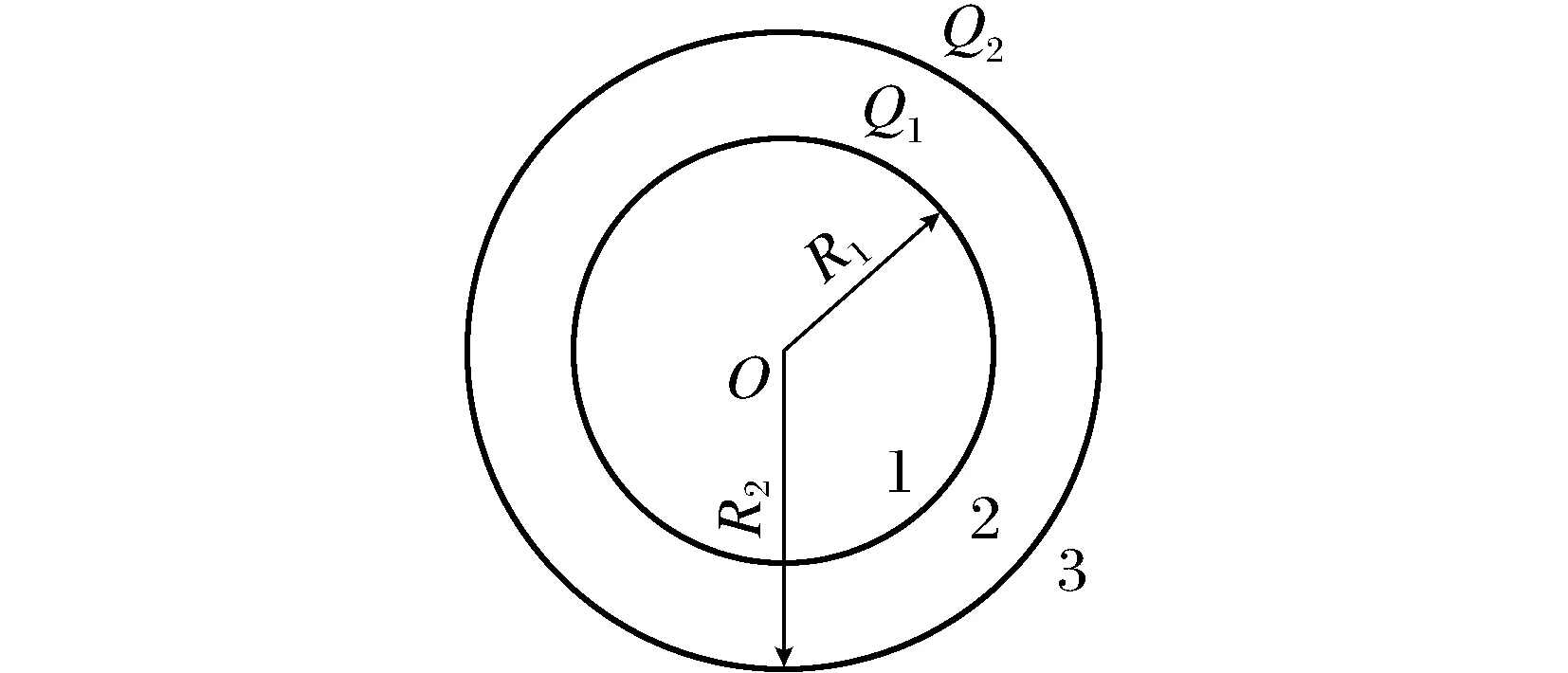
圖2 同心帶電球面Fig.2 Concentric charged spheres

1.3 等效法

所謂等效法,就是當電荷在某種特殊分布狀態下,對于一定的求解區域,可以將實際的電荷用一種更為簡單的、典型的分布來代替,而后者的解往往是已知的或更容易求解的。當電荷均勻分布于一個球面時,球外空間的電場可以等效于全部電荷集中于球心時的一個點電荷的電場,根據場強疊加原理,很容易給出上題中各區域的電場強度。這種等效的方法也適用于軸對稱和平面對稱的問題。

2 由電勢分布確定電場分布

電勢是描述靜電場性質的另一個物理量。它與靜電場的關系是

(6)

2.1 電勢疊加法

先考慮一個球面的電勢。如圖1所示,取環形面元dS=2π(Rsinθ)Rdθ,dq=σdS,σ=Q/4πR2。環形面上各點到場點的距離都相等,則有

積分得

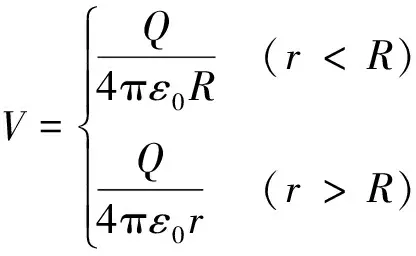
(9)

再由2個球面電勢疊加可得各區域電勢分布為

(10)

根據式(6),可求出3個區域的電場E1,E2,E3與前面結果完全相同。由于電勢是標量,所以在應用電勢疊加原理進行計算時要比應用電場疊加原理計算更為方便。式(7)應用了點電荷電勢公式,由于電荷分布在有限區域,所以選擇無窮遠點為電勢參考點,但如果帶電體無限大則不能這樣選擇。

2.2 分離變量法

分離變量法的思想是將物理問題轉化為邊值問題[14-16]。首先列出微分方程、邊值關系和邊界條件,然后寫出微分方程在所選坐標系中的通解,根據邊值關系和邊界條件確定通解中的待定系數。還是以上題為例,因界面形狀為球面,故選擇以O點為原點,任一半徑方向為極軸方向的球坐標系,列出該問題的全部定解條件:

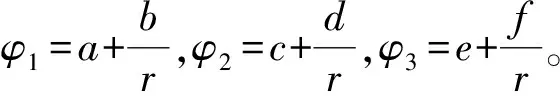
將上述系數代回到通解中即可確定各區域中的電勢,其情況與式(10)完全相同,再由式(6)可求得各區域靜電場與式(4)結果一致。分離變量法適用于求解區域沒有自由電荷分布的情況,此時滿足拉普拉斯方程,當界面是比較簡單的幾何曲面時,可求出靜電場的解析解。

3 結 論

通過以上論述及對特定球對稱問題的分析求解,可以使讀者了解多種求解靜電場的方法,開闊物理思維。在教學中,要使學生充分了解不同求解靜電場方法的基本原理、解題步驟以及不同方法的特點,提高綜合分析問題和解決問題的能力,針對不同的靜電場問題,能夠恰當選取適合的求解方法并熟練應用,也為今后解決實際靜電問題打下基礎。