一道零點個數問題的解法探究

廣東省惠州市第一中學 (516007) 黃偉才

題目函數f(x)=axex+lnx+x(a∈R).

(1)若a≥0，試討論函數f(x)的單調性；

(2)若f(x)有兩個零點，求a的取值范圍.

本題是廣東省珠海市2018屆高三3月質量檢測理科的壓軸題，表述簡潔，蘊含著豐富的數學思想，是一道入口寬，通法多的好題，全面考察了學生的導數與應用知識，還有函數與方程、化歸與轉化和數形結合等重要思想.這道題恰恰也是2017年全國I卷21題的改編題目，改后解法更豐富，且能更好考查學生對導數應用知識的掌握，所以筆者認為此題契合了全國卷命題風格，是一道以能力為立意的好題.本文談談我對這道題的一些思考，希望對讀者有所啟發.

一、解法探究

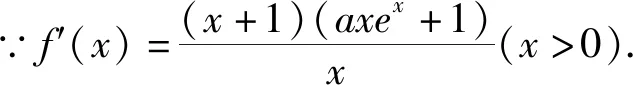
(1)若a≥0，易知f(x)在(0,+∞)單調遞增.

(2)∵f(x)有兩個零點，由(1)可知a<0，令g(x)=axex+1(x>0)，則g′(x)=a(1+x)ex<0，∴g(x)在(0,+∞)上單調遞減.∵g(0)=1>0，

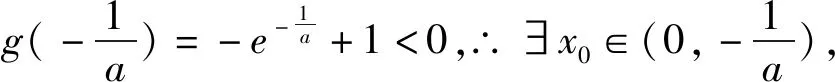
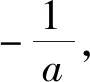
以上含參取點問題，應用分析法，執果索因，思路自然，所用思想方法易于理解，更能有效培養學生的分析問題、解決問題的能力及邏輯推理核心素養.

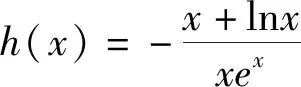
賞析2：當含參分類討論較復雜時，可以用分離變量來去避免討論，但要學生熟練掌握函數極限的判斷，甚至還要用到洛必達法則，這個中學數學教師特別喜愛的定理，可是由于高中階段洛必達法則沒有引入，所以高考中究竟如何才能拿滿分還值得商榷.

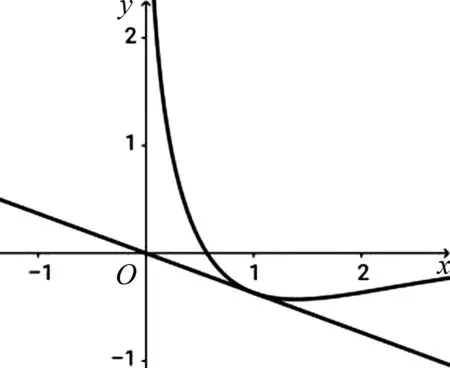
圖1

解法3：(局部分離參數)f(x)有兩個零點，可轉化為函數m(x)=

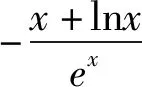
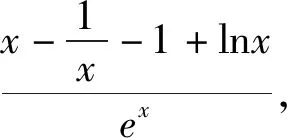
賞析3：合理分離構造函數，把函數零點問題轉化為兩個函數圖像交點問題，不過這類問題最好轉化為一次函數和非線性函數的交點問題，結合單調性和求切線可以順利解決，這里需說明所分離的函數圖像凹凸性才更加嚴謹.若要證明f(x)沒有零點，則還可以合理分離lnx和ex，構造非線性函數，利用函數凹凸反轉證明沒有交點，解題思想如2014年課標Ⅰ卷理科21題第2問.

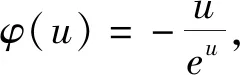
賞析4：這道題目入口之寬的精妙之處在于此，居然還可以用對數恒等式，等價轉化為復合方程解的個數問題.筆者姑且大膽猜測命題者編題是先由f(t)=aet+t零點個數，再令t=x+lnx，把原本簡單的問題通過對數恒等式包裝隱藏起來，進而得到函數f(x)=axex+lnx+x零點個數問題，變成一道難度極大的壓軸題.

二、教學啟示

從上述4種解法可以發現，本質上要用導數來研究函數圖像的形態，過程會涉及到分類討論，零點定理，隱零點問題，函數不等式比較大小，數形結合及合理分離構造函數等思想方法.當然本題還給筆者留下了如下啟示：

1.回歸教材 正本清源

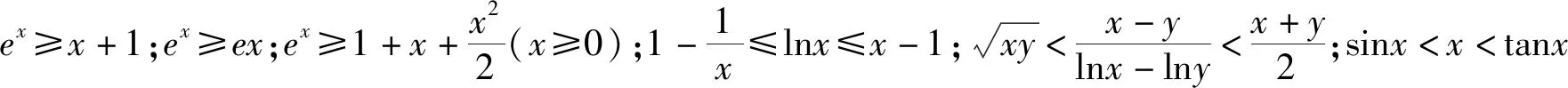
2.引導學生從一題多解過渡到多題一解