選煤廠原煤倉瓦斯超限治理研究

馬 恒，郭 瑤，梁騰飛，艾純明

(1.遼寧工程技術大學 安全科學與工程學院，遼寧 阜新 123000；2.礦山熱動力災害與防治教育部重點實驗室，遼寧 阜新 123000)

在選煤廠原煤倉中，煤粒的存在方式和采空區的遺落煤有相似之處，都屬于多孔介質的范疇[1]。前蘇聯學者[2]開創性地應用達西定律—線性滲透定律描述了瓦斯在煤層內的運動狀態；我國學者周世寧等[3]首次將多孔介質理論應用于煤層中，開辟了運用滲流理論治理煤層瓦斯的先河。針對原煤倉瓦斯超限問題，李丹天等[4]提出將通風口設置在原煤倉頂部的方案，以減少煤倉內積累的瓦斯，為原煤倉瓦斯的治理提出了新的優化思路；郭亞迪等[5]對原煤倉進行正壓通風和負壓抽風聯合改造，從理論上證明了混合式通風治理瓦斯的可行性；王兵建等[6]對圓筒煤倉倉下瓦斯積聚的原因和分布規律進行了研究，為選煤廠制訂防范措施提供了理論依據。筆者以鐵東選煤廠原煤倉為例，對原煤倉內部瓦斯涌出規律進行數值模擬，以期得出煤倉內部瓦斯的分布規律，通過對不同通風方式與風速的方案模擬結果進行分析對比，得出治理原煤倉瓦斯超限的優化方案，可為其他選煤廠原煤倉治理瓦斯超限提供參考。

1 選煤廠原煤倉數值模擬

1.1 數學模型的建立

原煤倉內部氣體的流動方式是間斷式流動，將其視為空氣在多孔介質區域的運動，使用間斷空間區域的計算方程[7]。使用模型為選煤廠原煤倉，由煤堆疊形成的空間可被視為多孔介質，其孔隙率取值范圍為0～1。

1)組分運輸方程

原煤倉內的氣體是空氣和瓦斯的混合氣體，而由于在原煤倉中堆疊的煤體會不斷地涌出瓦斯，改變了原煤倉內預混氣體的組分濃度[8]。在該過程中，所有組分之間符合組分質量守恒定律[9]：

(1)

式中：t為時間，s；ρ為氣體密度，kg/m3；Yi為質量分數；v為速度，m/s；Ri為反應產生凈速率；Si為組分生產率；Ji為擴散通量，由Fick定律[10-11]給出。

在湍流模型中，擴散通量表達式為：

(2)

式中：Di,m為質量擴散系數；μt為動力黏度，Pa·s；Sct為湍流施密特數，取值0.7；DT,i為熱擴散系數；T為溫度，K。

2)原煤倉控制微分方程

將原煤倉內空間看作具有梯度變化的滲流空間，通過引入的空度因子在多孔介質中應用質量守恒定律和納維斯托克斯方程[12-13]，假設氣體密度不發生改變，不受紊流效應的干擾，可以導出：

(3)

式中：ui、uj為速度分量，m/s；xi、xj為滲流方向；gi為加速度分量，m/s2；p為氣體壓力，Pa；μ為黏性系數，kg/(m·s)；Fi為瓦斯流動阻力，Pa/m。

1.2 原煤倉物理模型建立及邊界條件確定

物理模型選取鐵東選煤廠1號原煤倉，根據實際測量數據，將原煤倉分為3個部分：第1部分為原煤倉放煤口的倒圓臺形結構，圓臺高8 m，上、下部直徑分別為20、3 m；第2部分為圓柱體結構，高度為38 m，其直徑與圓臺上部直徑相同；第3部分為圓柱體結構，其上部的3個正方形窗口，邊長為3 m，其中2個對立的窗口為通風口，另一個窗口為原煤進口。倉內為半封閉狀態，底部煤體賦存了大量瓦斯，易導致煤倉內瓦斯濃度(甲烷體積分數，下同)超標，遇明火易引發爆炸事故。

采用有限體積法中的拓撲劃分方式對原煤倉進行網格劃分，采用自適應性網格。網格總數為20萬個，將原煤倉劃分成12個區域，第1部分底部區域劃分為 44 644個網格；第2部分圓柱體部分劃分為10個區域，且每個區域網格數量一致，均為 11 065個；第3部分中通風口和進煤口附近區域劃分為 9 751個網格。原煤倉網格劃分如圖1所示。

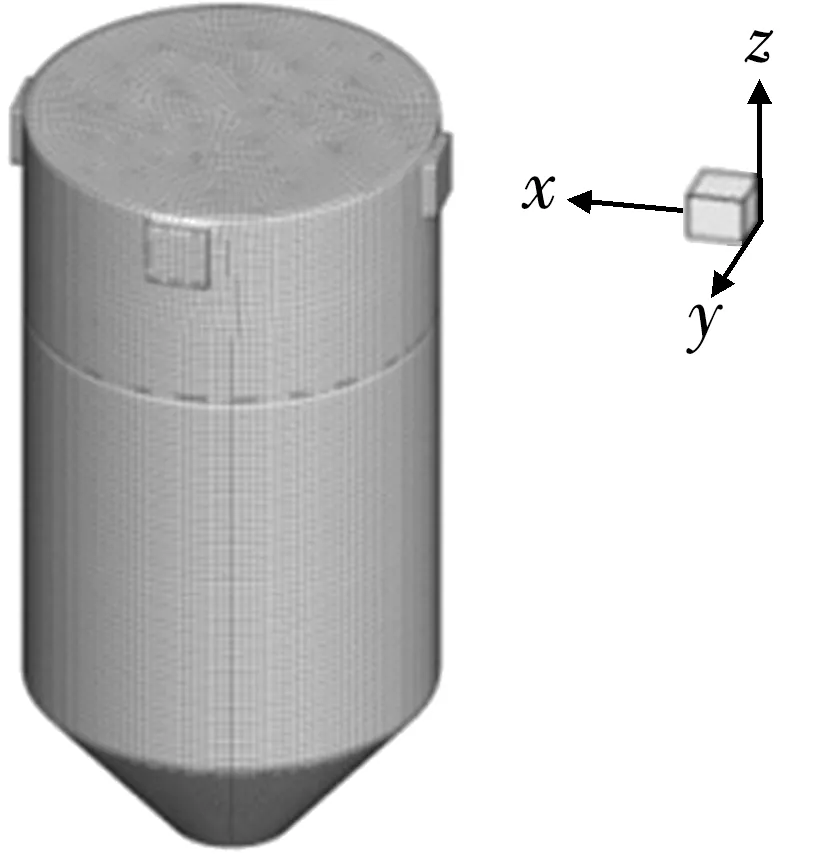
圖1 原煤倉網格劃分圖

邊界條件主要為進出風口，將進煤口設定為風量進口，采用速度入口的方式，即VELOCITY-INLET；2個出風口不采取機械通風的方式，而是將其定義為自由出口，且出口使用率為1。數值模擬條件設置情況見表1。

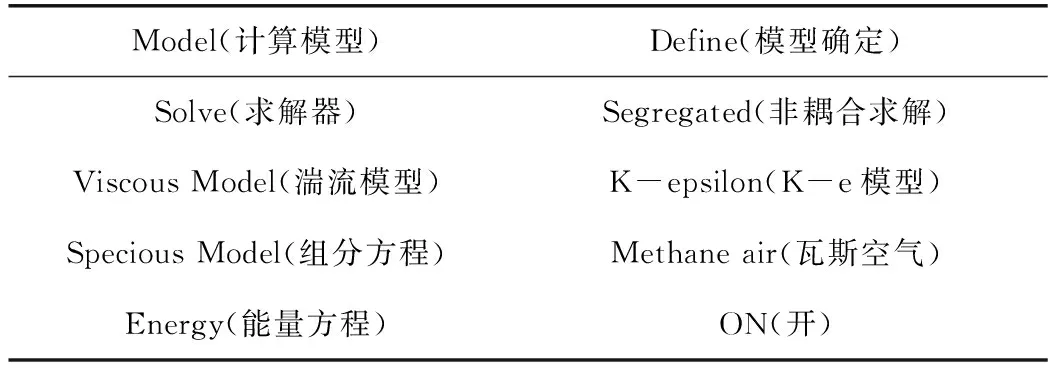
表1 數值模擬條件設定

多孔介質孔隙率計算公式如下：

q=1-1/kp

(4)

式中：q為多孔介質孔隙率；kp為碎脹系數，取經驗值1.3。

通過計算得到原煤倉煤體之間的孔隙率q=0.231。原煤倉內煤堆疊的方式呈線性變化，因此孔隙率也呈線性變化，在物理建模和網格劃分過程中單獨定義12個計算區域的孔隙率，將h=15 m處計算區域的孔隙率設為0.231，計算區域每升高或降低一個區域孔隙率增加或減少0.020，其值增加或減少0.020，這樣可保證模擬結果的準確性。

原煤倉內涉及多孔介質流動問題，將黏性損失與慣性損失之和作為動量守恒方程[14]中的附加動量損失源項。1/k為黏性損失系數，f為慣性損失系數，其計算公式如下：

(5)

(6)

式中：k為多孔介質滲透率，m2；b為原煤倉煤體平均粒徑，m。

1.3 原煤倉源項確立

為研究瓦斯在原煤倉內的運移規律，在原煤倉進煤口進行實地采樣，原煤倉內部瓦斯的平均涌出量[15]Q0如表2所示。

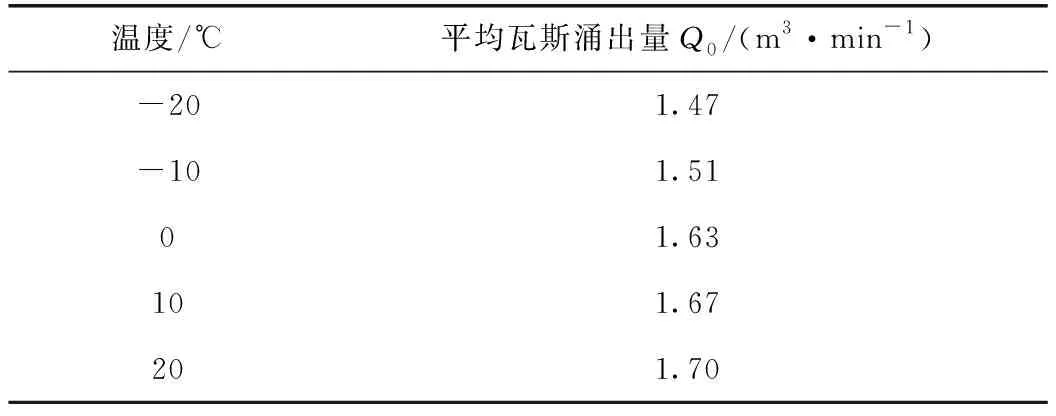
表2 原煤倉瓦斯涌出量

通過計算得到原煤倉內瓦斯密度ρ為0.7 kg/m3，原煤倉內煤體的總體積Vc為9 420 m3，在Fluent模擬計算中煤體解吸出的瓦斯量q源被視為源項，其計算公式如下：

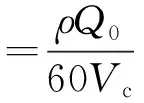
(7)

式中：q源為原煤源項，kg/(m3·s)；Q0為瓦斯的平均涌出量，m3/min。

1.4 數值模擬及結果分析

不借助任何通風設備，模擬自然條件下原煤倉的瓦斯運移情況。根據鐵東選煤廠所處環境的年平均氣溫變化，得到該地區夏季室外平均氣溫為20 ℃，該溫度下原煤倉內瓦斯濃度(CH4體積分數，下同)的模擬結果見圖2。

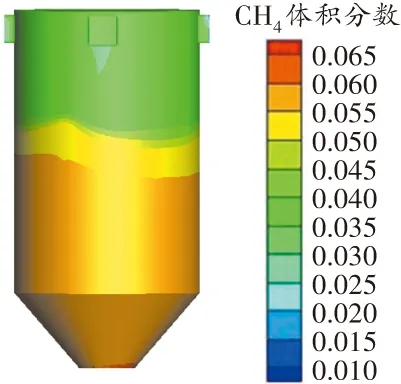
圖2 20 ℃時原煤倉內瓦斯濃度分布三維云圖

該地區冬夏兩季室外平均氣溫溫差較大，冬季室外的平均氣溫為-20 ℃，該溫度下原煤倉內瓦斯濃度的模擬結果見圖3。

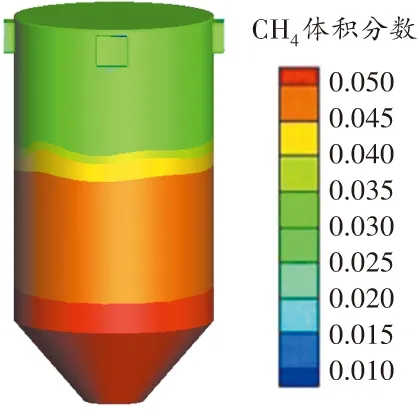
圖3 -20 ℃時原煤倉內瓦斯濃度分布三維云圖

由圖3可知，根據原煤倉內瓦斯濃度，由上至下可將原煤倉劃分為4個區域：中空區、自然堆積區、亞壓實區、壓實穩定區。其中中空區位于原煤倉頂部至下方10 m處，該區域為流體流動區域，區域內氣體成分為瓦斯和空氣；自然堆積區位于中空區下方邊緣處至其下方3 m處，該區域煤體相對松散，在整個煤體中孔隙率最大，瓦斯在該區域的上升過程中阻力最小，因此該區域內瓦斯濃度相對較低。隨著原煤倉內煤體體積增加，煤體間的縫隙減小，煤體釋放的瓦斯不能迅速擴散，會在倉底積聚，所以在整個原煤倉內倉底處的瓦斯濃度是最高的。

由圖2、圖3可知，在冬季原煤倉中空區的瓦斯濃度大于3.0%，而夏季瓦斯濃度大于4.0%，位于原煤倉內底部儲煤區域的瓦斯濃度大于5.0%。瓦斯濃度在中空區呈線性變化，該區域內瓦斯濃度與原煤倉高度呈正比關系，而該變化關系僅適用于原煤倉體內部，而在通風口處的瓦斯濃度比同高度原煤倉內部的瓦斯濃度低，在整個原煤倉內瓦斯濃度最低，約為3.2%。

根據上述模擬結果，對照《煤礦安全規程》(以下簡稱“規程”)[16]，該原煤倉內中空區內的瓦斯濃度已超過規程限定值(1%)，表明該原煤倉上方非煤區域內瓦斯濃度明顯超標。因此可判定該原煤倉處于瓦斯超限狀態，該選煤廠存在安全隱患。

1.5 實測數據對比

采用瓦斯濃度傳感器對原煤倉中空區的瓦斯濃度進行實時監測，傳感器安裝于膠帶支架上，瓦斯濃度傳感器布置如圖4所示。

圖4 瓦斯濃度傳感器平面布置圖

為驗證數值模擬結果的準確性，將改造前原煤倉內瓦斯濃度變化的實時監測數據(2017年7月 25日)與數值模擬結果進行對比，繪制出瓦斯濃度隨時間變化的對比圖，如圖5所示。

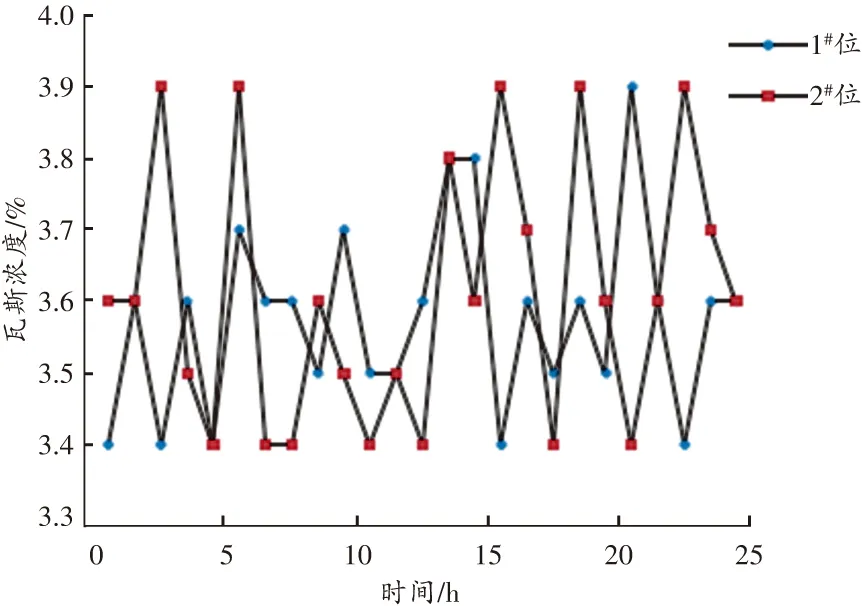
圖5 瓦斯濃度隨時間變化對比圖

模擬所得該原煤倉中空區夏季的瓦斯濃度為3.6%，而實際監測數據顯示該區域的瓦斯濃度在3.6%上下波動，二者結果基本一致，表明本文采用的數值模擬方法是準確的。

2 選煤廠原煤倉瓦斯超限治理方案

模擬結果及實測結果表明該選煤廠原煤倉的瓦斯超標情況較嚴重，需要對原煤倉采取措施，以滿足規程要求。筆者從安全和經濟的角度出發，通過增加原煤倉通風口的數量,以及倉外通風設施對原煤倉進行優化改造，采用4種優化方案并進行模擬，通過對比和分析，選取最優的解決方案，以解決該原煤倉瓦斯超限的問題。

2.1 一進兩出、正壓通風可行性分析

1)方案1：正壓通風，風速為1.0 m/s。

在原煤倉現有結構的基礎上，添加風機，向煤倉內進行正壓通風，風速為1.0 m/s。兩側窗體結構為風流的自由出口，將煤倉內的預混氣體排出煤倉體，降低煤倉內的瓦斯濃度。該模擬過程中環境溫度為20 ℃，模擬結果如圖6～8所示。

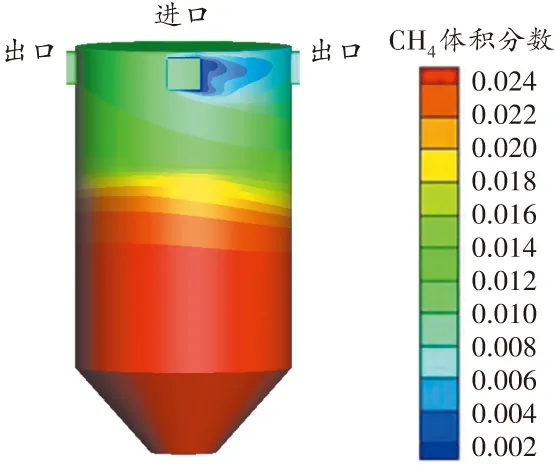
圖6 正壓風速1.0 m/s時原煤倉瓦斯濃度分布三維云圖

圖7 正壓風速1.0 m/s時原煤倉z=38 m位置速度矢量圖

圖8 正壓風速1.0 m/s時原煤倉z=35 m位置速度矢量圖

由圖6可知，通風過程中原煤倉倉底的瓦斯濃度小于2.4%，而中空區的瓦斯濃度為1.2%，部分區域的瓦斯濃度仍然超過規程限定的數值。

由圖7、圖8可知，在35 m以上區域存在局部阻力，因此產生了兩處渦流，瓦斯在該區域出現了積聚現象，因此方案1無法解決原煤倉瓦斯超限的問題。

2)方案2：正壓通風，風速為1.6 m/s。

不改變方案1的邊界條件，只增大進口處的風流速度，將風速提高至1.6 m/s，模擬結果如圖9 所示。

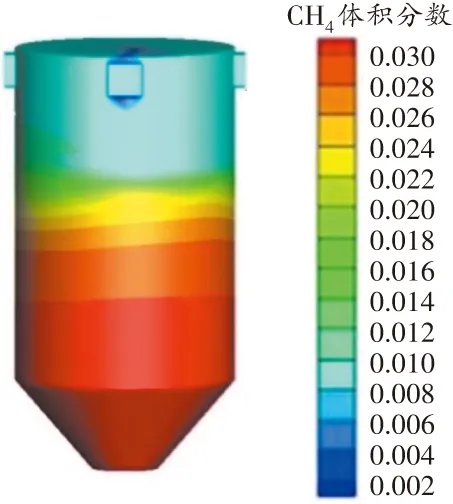
圖9 正壓風速1.6 m/s時原煤倉瓦斯濃度分布三維云圖

由圖9可知，方案2未能改變壓實穩定區的瓦斯濃度，因此壓實穩定區瓦斯濃度小于3.0%；而中空區的瓦斯濃度降低至0.8%，表明原煤倉內瓦斯濃度處于安全生產規程范圍內。

通過對比方案1、2的模擬結果可知，方案2符合安全生產規程。由于低風量能降低煤倉內煤與氧氣發生氧化反應的概率，也會減少煤的風化過程，因此需提出減小風量的方案，以達到安全生產要求。

2.2 兩進兩出、正壓通風可行性分析

在原煤倉現有結構的基礎上，增加煤倉通風口的數量，使其通風方式為對稱通風，同時增加通風機數量，每個通風機對應一個通風出口。

1)方案3：正壓通風，風速為0.5 m/s。

新的物理模型的網格劃分方式與原物理模型一致，如圖10所示。將2個進口的風速均設置為 0.5 m/s，模擬結果如圖11～13所示。

圖10 原煤倉網格劃分圖Ⅱ

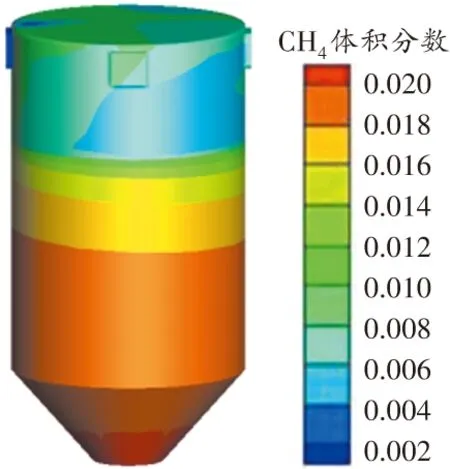
圖11 正壓風速0.5 m/s時原煤倉內瓦斯濃度分布三維云圖

圖12 正壓風速0.5 m/s時原煤倉內z=38 m位置速度矢量圖

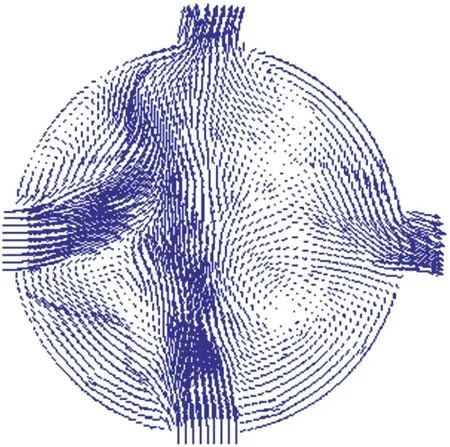
圖13 正壓風速0.5 m/s時原煤倉內z=35 m位置速度矢量圖

由圖11可知，儲煤區是原煤倉中瓦斯濃度最高的區域，該區域瓦斯濃度為2.0%，原煤倉的瓦斯濃度由上至下逐漸減小，煤體上部與空氣接觸的部位瓦斯濃度最低為1.2%；中空區部分瓦斯濃度雖略有差別，但總體不超過1.0%，進風口處是瓦斯濃度最高的區域，瓦斯濃度大于1.0%。

由圖12、圖13可知，中空區的阻力較小，沒有產生明顯的氣流渦旋，導致進風口區域之間瓦斯濃度略高的原因是類似于風流經過障礙物后速度減小導致微風區效應的產生，這部分區域氣體的流動較緩慢，聚積的瓦斯不能快速被風流稀釋排出煤倉外。

2)方案4：正壓通風，風速為0.7 m/s。

在方案3的基礎上增大風流速度，每個進風口的風流速度增加至0.7 m/s，模擬結果如圖14～16所示。

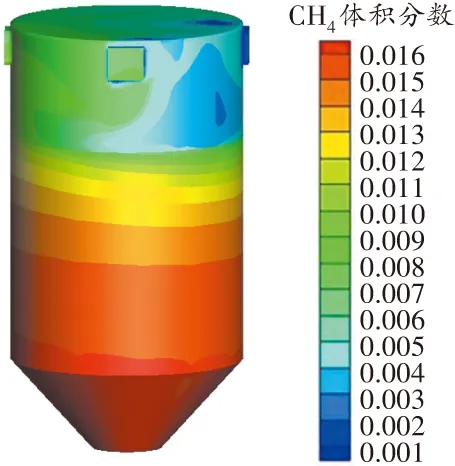
圖14 正壓風速0.7 m/s時原煤倉內瓦斯濃度分布三維云圖

圖15 正壓風速0.7 m/s時原煤倉內z=38 m位置速度矢量圖

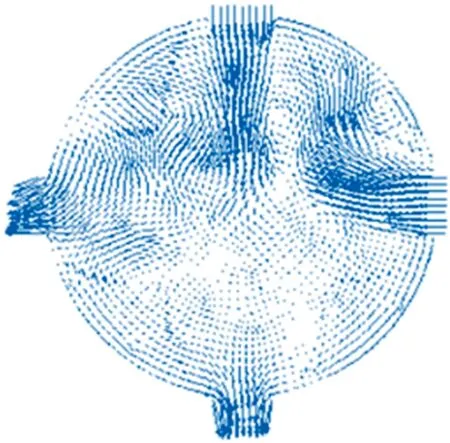
圖16 正壓風速0.7 m/s時原煤倉內z=35 m位置速度矢量圖

由圖14可知，原煤倉中瓦斯濃度最高值為1.6%，煤倉內瓦斯濃度基本符合安全生產規程要求，中空區的瓦斯濃度小于1.0%。

由圖15、圖16可知，在該通風方式下，煤倉內局部阻力較小，中空區不存在氣流渦旋現象，風流分布較為均勻。

方案4是理論上最為理想的優化方式，既降低了中空區的瓦斯濃度，又使煤倉內煤體的瓦斯濃度符合規程規定值、進風量減少，所以該方案為治理原煤倉瓦斯超限的最優方案。

2.3 煤倉風量需求確定

在夏季通風過程中，方案4所需的最大風量Q=756 m3/min。在冬季煤體瓦斯的釋放速度較緩，可降低通風需求，采用方案4的邊界條件對-20 ℃時的原煤倉進行數值模擬研究，設置進口風速為0.5、0.6 m/s。模擬結果如圖17～18所示。

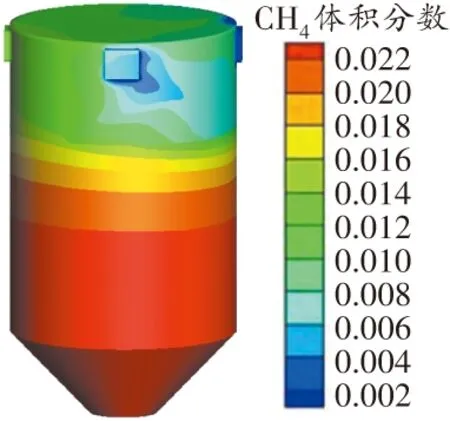
圖17 冬季風速0.5 m/s時原煤倉內瓦斯濃度分布三維云圖

由圖17、圖18可知，當風速為0.5 m/s時可以滿足壓實穩定區的瓦斯濃度要求，但中空區的瓦斯濃度超標；當風速為0.6 m/s時，原煤倉各處的瓦斯濃度均符合安全生產要求。

通過模擬可知，原煤倉處于-20 ℃低溫環境時，通風量要小于20 ℃正常室溫時的通風量，該條件下所需通風量Q為648 m3/min。

3 結論

1)通過建立原煤倉的物理模型，采用數值模擬方法得到原煤倉內瓦斯的分布狀態，瓦斯濃度呈梯度分布，自上至下逐漸增高，由上至下可將原煤倉劃分為4個區域，即中空區、自然堆積區、亞壓實區、壓實穩定區，從儲煤區域涌出的瓦斯會聚積在原煤倉頂部的中空區。

2)對選煤廠原煤倉數值模擬結果及現場實測數據進行對比分析，驗證了數值模擬結果和數值模擬手段的準確性。

3)增加通風口數量，形成進出比例相同的通風系統，根據室外溫度的不同，定義不同的進風速度，根據安全生產規程規定的原煤倉瓦斯濃度得到冬夏兩季的進風速度為0.7、0.6 m/s。