LMD-KICA 滾動軸承信號特征提取方法研究

張炎磊，張培杰，方雁衡，董辛旻

（1.鄭州大學振動工程研究所，河南 鄭州 450001；2.鄭州市質(zhì)量技術(shù)監(jiān)督檢驗檢測中心，河南 鄭州 450053；3.廣東省特種設(shè)備檢測研究院順德檢測院，廣州 佛山 528300）

1 引言

大型工程機械中的滾動軸承應用廣泛，并且使用頻率高，同時也是零部件中極易發(fā)生損害的一種，并且當滾動軸承產(chǎn)生故障時容易引發(fā)其他故障，甚至引起整個設(shè)備的失效，所以軸承的運轉(zhuǎn)情況極大地影響機械的運行狀況[1]，因此近些年來對軸承的監(jiān)測和診斷的關(guān)注度越來越高。當滾動軸承出現(xiàn)故障時，非平穩(wěn)信號占據(jù)故障信號的絕大部分，同時在實際工程中，大型機械的運行往往伴隨的大量的噪聲信號，因此滾動軸承故障診斷的重點在對滾動軸承噪聲處理后的信號特征提取。

近些年來，非平穩(wěn)信號的處理越來越多元化，自適應時頻分析方法發(fā)展尤為迅速且更適合非平穩(wěn)信號的處理。自適應分析方法的研究中，在EMD 方法的研究基礎(chǔ)上，文獻[2]于2005 年提出了局部均值分解（LMD）。它在不丟失信號信息的基礎(chǔ)上，根據(jù)信號自身特點，將信號分解成多個以純調(diào)頻信號和包絡(luò)信號為基礎(chǔ)的PF 分量。在此基礎(chǔ)上，文獻[3]將獨立分量分析方法（ICA）的優(yōu)勢結(jié)合局部特征分解，再根據(jù)相關(guān)系數(shù)準則對故障信號處理，完成對信號的降噪以及特征提取。同時根據(jù)文獻[4]研究，以及文獻[5]的對比研究，核獨立分量分析（KICA）更加適用于實際工業(yè)過程中的非線性信號，KICA 模型相對于ICA 模型在對故障反應更加靈敏，故障信號的區(qū)分度也更加明顯。

結(jié)合LMD 方法和KICA 模型的優(yōu)勢，針對滾動軸承故障信號特點，提出了一種基于LMD-KICA 的特征提取方法。并且用此方法對滾動軸承進行仿真信號分析和西儲大學滾動軸承故障實驗數(shù)據(jù)分析，再通過對比同類型的其他特征提取方法，驗證了方法的適用性。

2 理論基礎(chǔ)

2.1 局部均值分解（LMD）

局部特征尺度分解方法是根據(jù)被處理信號本身的特性，將信號根據(jù)尺度不同分解成一系列的由純調(diào)頻信號和包絡(luò)信號組成的PF 分量，并且可達到信號特征信息不丟失[6]。對于信號x（t），LMD 分解過程如下所示：

定位信號x（t）所有極值點，求得兩兩相鄰極值點的局部均值和其包絡(luò)估計值。

式中：mi—相鄰極值點的局部均值；ai—局部均值的包絡(luò)估計值；

ni—所有的局部極值點；ni+1—ni相鄰的極值點。

對mi，ai分別進行直線擬合和滑動平滑處理以獲得各局部均值函數(shù)m11（t）和包絡(luò)估計函數(shù)a11（t）。

由式（3）、式（4）可得：

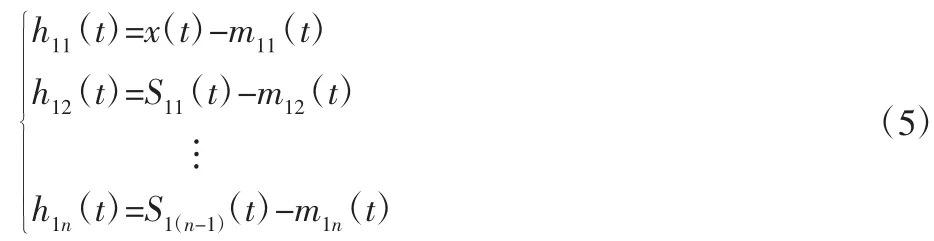
式中：h1i（t）—源信號中移除m1i（t）得到；s1i（t）—h1i（t）解調(diào)信號。

直至函數(shù)a1n（t）滿足1-Δ≤a1n≤1+Δ 時中止迭代，得到最終包絡(luò)信號：

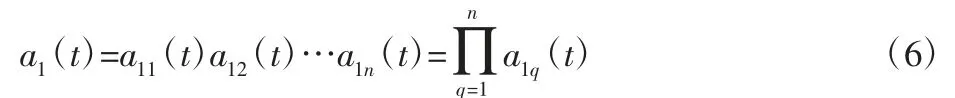
將得到的a1（t）和s1n（t）相乘，得到第一個PF 分量：

從源輸入信號x（t）中去除PF1（t），得新信號u1（t）：

將信號u1（t）重復（1）到（8）式過程進行處理，得到其他PF 分量。重復k 次，當uk（t）的極值點數(shù)為1 或0 時停止，得到殘余項。此時源信號可以轉(zhuǎn)換為k 個PF 分量和殘差之和，如下面的等式所示：

2.2 核獨立分量分析

在獨立分量分析（ICA）的研究上，加以改進并發(fā)展得到新的核獨立分量分析方法（KICA），適用于超高斯信號和亞高斯信號及分布的非線性算法。原理是重新定義重構(gòu)希爾伯特空間的對比度函數(shù)，優(yōu)化對比度函數(shù)算法以獲得分離矩陣并獲得估計源，可以根據(jù)有限數(shù)量的觀察矢量樣本有效地解決混合信號，以獲得分離的有效信號。鑒于核函數(shù)所長，核獨立分量分析通過非線性映射和解混合矩陣將非線性信號從低維原始空間轉(zhuǎn)換為高維線性特征空間[7-8]。經(jīng)過計算（具體算法分析和步驟參見文獻[9]），最終得到較好的分離信號。

2.3 LMD-KICA 特征提取方法流程

滾動軸承的故障時常發(fā)生，結(jié)合產(chǎn)生時的特點，故障信號成分比較復雜且易被噪聲干擾，有效的故障信號和特征信息極易被噪聲信號所干擾，提出基于LMD-KICA 方法提取故障特征。首先將源信號進行LMD 分解，根據(jù)相關(guān)系數(shù)準則提取相關(guān)程度高的的PF 分量并構(gòu)建新的信號，對新構(gòu)建的故障信號運用KICA 進行噪聲分離，進而獲得故障信號特征。具體流程圖，如圖1 所示。

圖1 算法流程圖Fig.1 Algorithm Flowchart

3 仿真分析

為了體現(xiàn)LMD-KICA 方法對信號故障分離的效果，同時對比LMD-ICA，體現(xiàn)這里方法的優(yōu)越性，構(gòu)造如下仿真信號：

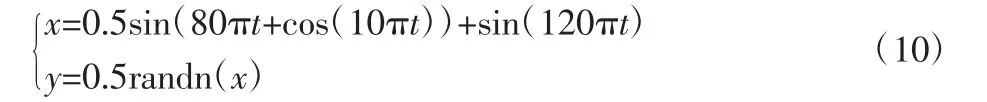
由（10）式知：構(gòu)造信號的采樣頻率Fs=2048Hz，采樣點數(shù)n=215，x 信號為故障信號，y 信號是隨機的噪聲信號。x、y 信號的源信號時頻域圖，如圖2 所示。將x、y 信號隨機混合得到一個新的信號，則該混合新信號的時頻域圖，如圖3 所示。

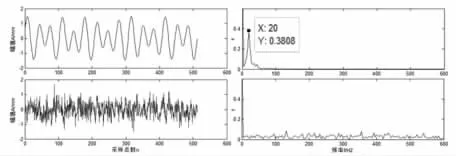
圖2 源信號Fig.2 Source Signal

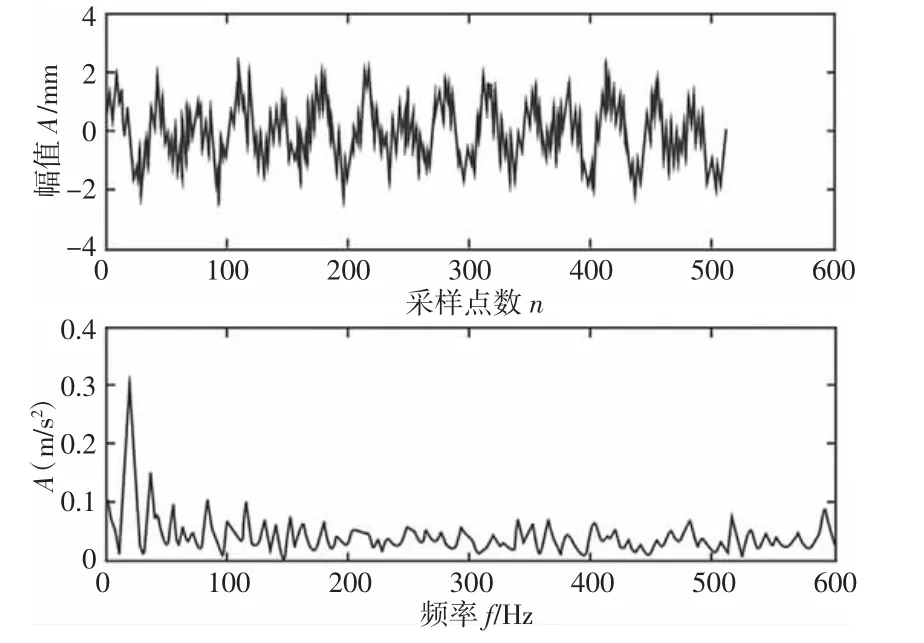
圖3 混合信號Fig.3 Fusion Signal

對該新信號通過LMD-KICA 方法進行噪聲分離，并根據(jù)相關(guān)系數(shù)準則提取相關(guān)程度高的的PF 分量并構(gòu)建新的信號，對新構(gòu)建的故障信號運用KICA 處理后的兩觀測信號的時頻域圖，如圖4 所示。

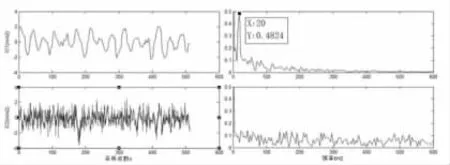
圖4 LMD-KICA 分離信號Fig. 4 LMD-KICA Separation Signal

通過圖4 可得，分離處理后的兩信號中，通過頻域信號可得IC1 信號中包含故障信號信息更加明顯，IC2 信號基本有噪聲信號組成，且IC1 時域信號相對平滑，更接近原故障信號。

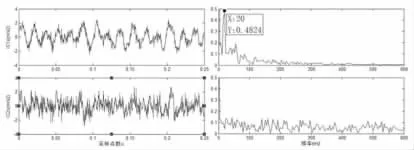
圖5 LMD-ICA 分離信號Fig. 5 LMD-ICA Separation Signal

同時為體現(xiàn)這里方法的適用性和優(yōu)越性，對混合信號進行LMD-ICA 方法處理，得其時域頻域圖，如圖5 所示。對比圖4、圖5 可知，LMDD-KICA 處理后的IC1 分量的時域信號相對于IC2 分量更加平滑，更接近源信號，同時頻域信號中含有噪聲信號較少。根據(jù)仿真分析結(jié)果可知，對于非線性混合信號，LMD-KICA 算法分離效果較好。

4 實驗研究

圖6 實驗裝置系統(tǒng)Fig.6 Experimental Device System

為證明LMD-KICA 算法處理滾動軸承信號的適用和優(yōu)越性，這里使用Case Western Reserve University 滾動軸承試驗臺一組測量故障數(shù)據(jù)進行實驗分析[10]，實驗系統(tǒng)，如圖6 所示。實驗臺由1.5KW 電動機，扭力傳感器和一個功率計組成，使用試驗臺電動機驅(qū)動端軸承信號進行分析。電機驅(qū)動端的軸承通過電火花點損待檢測軸承來設(shè)置故障點。故障滾動軸承型號為SKF6205 深溝球軸承，滾動體數(shù)量為9，滾動體直徑為7.94mm，內(nèi)圈直徑為25mm，外圈直徑為52mm，接觸角為0°。信號檢測采用加速度傳感器，安裝在電動機驅(qū)動端軸承座正上方的軸承座位置。試驗臺軸承的振動信號通過16 通道數(shù)據(jù)記錄器采集記錄，功率和轉(zhuǎn)速通過扭力傳感器測得。電動機轉(zhuǎn)速1796r/min，驅(qū)動端軸承故障數(shù)據(jù)以12000S/s 的采樣速率采集。

由于本實驗系統(tǒng)采集的故障信號中內(nèi)圈早期故障信號更加明顯，研究所選取內(nèi)圈故障信號對算法加以計算分析。通過理論計算得到軸承內(nèi)圈故障頻率約為162.19Hz，采樣點數(shù)為4096，內(nèi)圈故障信號的時頻域圖，如圖7 所示。

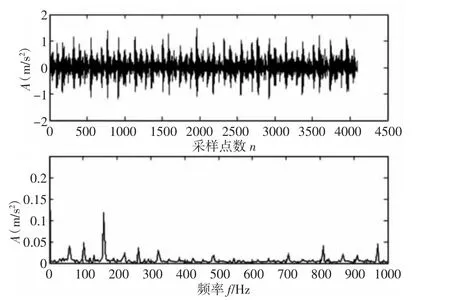
圖7 內(nèi)圈故障信號時頻域圖Fig.7 Inner Loop Fault Signal Time Domain Frequency and Domain

為了驗證該方法，將故障信號進行LMD 分解，并根據(jù)相關(guān)系數(shù)，計算出各個PF 分量與源信號的相關(guān)系數(shù)，選擇具有高相關(guān)性的PF 分量重新組合以構(gòu)建新信號。

根據(jù)計算3 階以上分量相關(guān)程度較低，因此選取LMD 分解的前3 個分量，如圖8 所示。

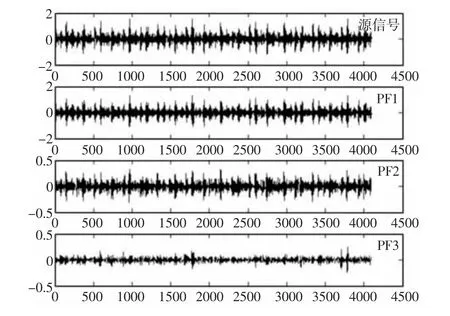
圖8 源信號及各PF 分量Fig.8 Source Signal and Each PF Component

通過相關(guān)系數(shù)準則，計算得前3 階PF 分量的相關(guān)系數(shù)，如表1 所示。

表1 各PF 分量與源信號相關(guān)系數(shù)Tab.1 Correlation Coefficient of Each PF Component and Source Signal

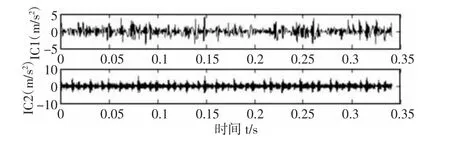
圖9 KICA 分量時域圖Fig.9 KICA Component Time Domain Diagram

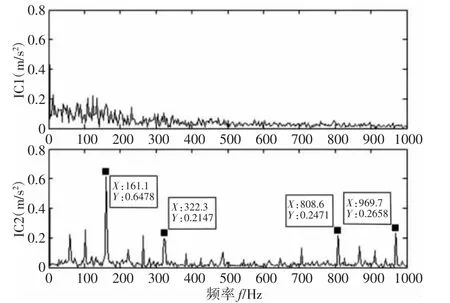
圖10 KICA 分量頻域圖Fig.10 KICA Component Frequency Domain

從表1 可以看出，PF1 和PF2 的兩個分量相關(guān)系數(shù)大于0.3，相關(guān)程度達到實相關(guān)以上，與源信號的相關(guān)程度高，保留了源信號的更多信息，PF3 僅達到微相關(guān)度。因此根據(jù)相關(guān)程度高低分別將PF1+PF2 和PF3 重構(gòu)為兩組信號，再經(jīng)KICA 算法得到核獨立分量信號IC1、IC2 時域、頻域圖，如圖9、圖10 所示。由圖9、圖10 可得，KICA 處理后較為理想地分離出噪聲信號，IC1 分量顯而易見的是噪聲信號，其中并不能發(fā)現(xiàn)故障特征成分，IC2 分量明顯可觀察到故障頻率f=161.1HZ，3 倍頻f=322.3HZ，5 倍頻f=808.6HZ，6 倍頻f=969.7HZ 處故障頻率與原信號對比更加突出，故障特征更加明顯。同時為了對比分析，對故障信號使用LMD-ICA 處理，得到獨立分量信號的時域、頻域圖，如圖11、圖12 所示。對比時域信號圖9、圖11，不難發(fā)現(xiàn)經(jīng)KICA 處理后的兩個分量中有明顯的區(qū)分度，IC1 分量相比而言更加嘈雜；而ICA 分量時域圖中的兩個分量信號則難以區(qū)分；再次對比頻域信號圖10、圖12，我們可以輕易發(fā)現(xiàn)KICA 分量的故障成分更加突出，同時經(jīng)ICA 處理后的的IC2 分量清楚地顯示故障信號中仍然包含部分5 倍頻f=808.6HZ 成分，表明ICA 分解并不能完全分離出故障信號。因此，對于更復雜的故障信號，LMD-ICA 算法不能很好地執(zhí)行信噪比分離，而經(jīng)過驗證LMD-KICA 方法對比較復雜的非線性信號具有更好的分離能力。

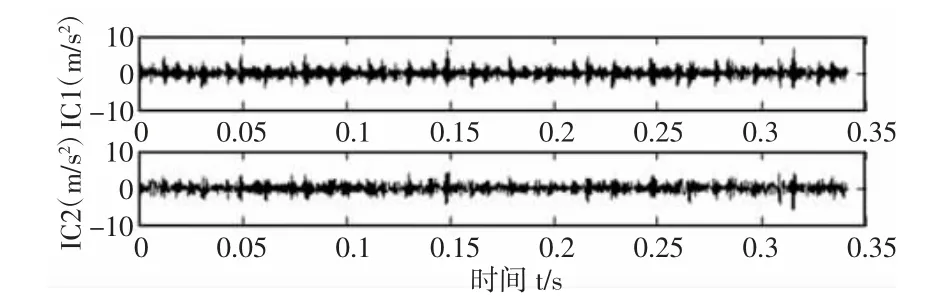
圖11 ICA 分量時域圖Fig.11 ICA Component Time Domain Diagram

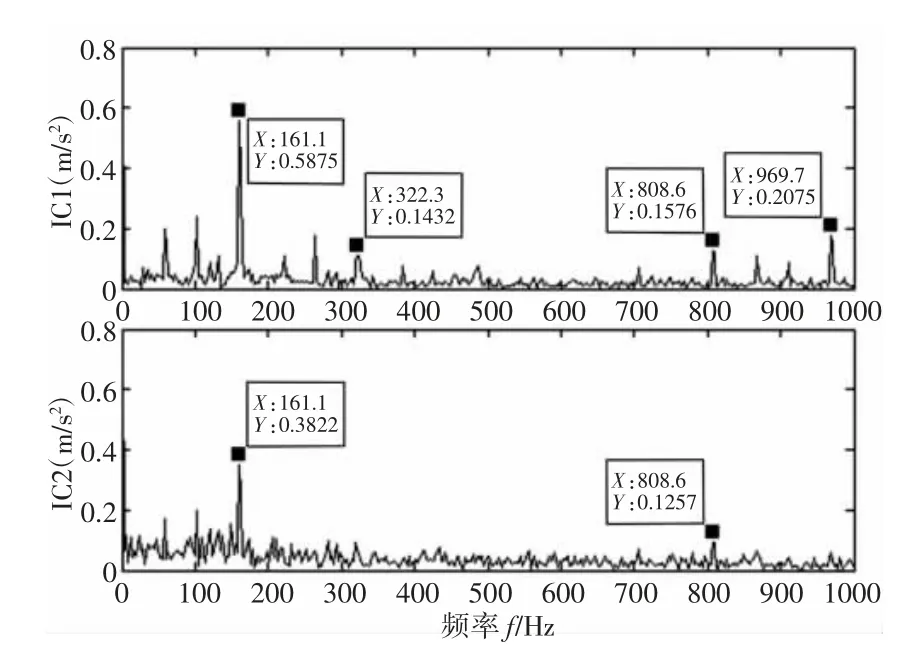
圖12 ICA 分量頻域圖Fig.12 ICA Component Frequency Domain

綜上所述，經(jīng)LMD-KICA 方法處理后的故障信號中，其頻域信號可以準確分離故障信號和噪聲信號，在復雜的非線性信號中進行特征提取具備一定優(yōu)勢。為驗證LMD 分解的優(yōu)勢，根據(jù)文獻[5]的研究，對比分析了ITD 與EMD 方法，其中ITD 方法更具優(yōu)勢，而經(jīng)EMD 處理后的故障信號振幅較小且故障特征不明顯。在此直接引用分析結(jié)果，在此對故障信號使用ITD-KICA 處理，得到獨立分量信號的頻域圖，如圖13 所示。對比圖10 和圖13，粗略觀察不難發(fā)現(xiàn)ITD 方法和LMD 方法在信噪分離結(jié)果方面比較接近，但相對ITD-KICA 處理結(jié)果而言，LMD-KICA 方法處理后的故障信號除2 倍頻處的其他故障信號1 倍頻、5 倍頻，6 倍頻處振幅都較高，包含故障特征更明顯。因此就最后KICA 分量頻域結(jié)果方面來說，LMD 分解較ITD 與EMD 方法更具優(yōu)勢。

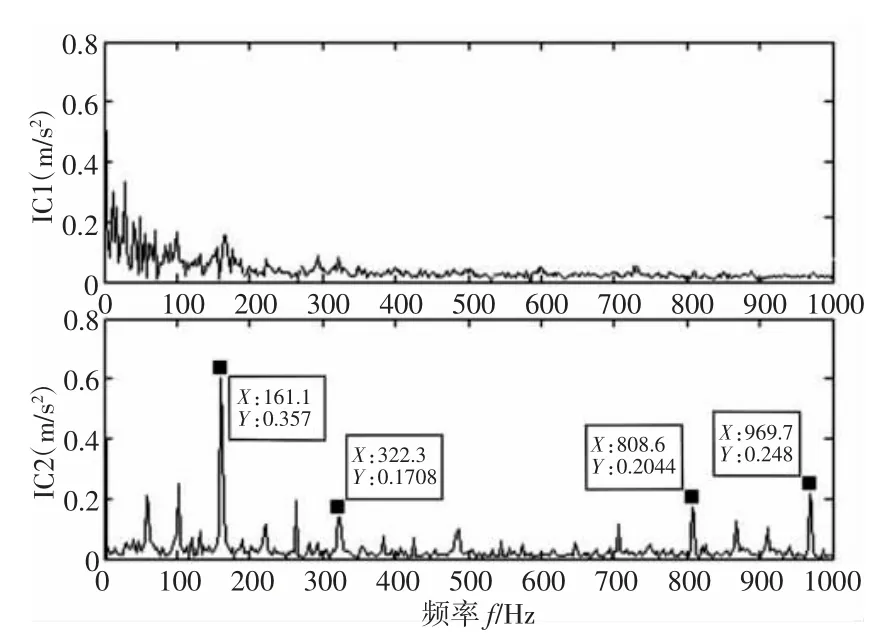
圖13 ITD-KICA 分量頻域圖Fig.13 ITD-KICA Component Frequency Domain

5 結(jié)論

通過綜上所述研究，提出了一種針對于滾動軸承的LMDKICA 結(jié)合的故障特征提取方法。該方法根據(jù)滾動軸承故障信號數(shù)據(jù)的復雜和非平穩(wěn)特性，首先通過LMD 對信號進行分解，提取故障信號中的有效成分，并根據(jù)互相關(guān)準則利用具有較多故障的分量重構(gòu)該分量，最后運用KICA 方法對新重構(gòu)信號信噪分離，解除了信噪比對有效故障成分的影響，有效提高故障信號的特征信息。將LMD-KICA 方法對比LMD-ICA 方法，通過仿真分析驗證方法有效性，并通過凱斯西儲大學軸承實驗數(shù)據(jù)對比LMDICA、ITD-KICA 與EMD-KICA 方法驗證，證明LMD-KICA 方法對較復雜的非線性信號具有更好的分離提取能力。