自動化裝配機器人加工站位跟蹤控制方法

李曉東

（鄭州商學院 信息與機電工程學院，鄭州 451200）

0 引言

自動化裝配機器人由操作機、控制器、末端執行器以及傳感系統等多個部分組成，其是自動化裝配制造系統的關鍵結構之一。該類機器人具有高精度、高匹配性的優勢，能夠在較小的范圍內作業，也可與其他系統配合作業[1]。

在作業過程中，機器人能夠完成對不同尺寸大小目標對象的加工。在目標對象尺寸較小時，機器人在固定的位置就能完成所有的加工任務。如果加工的目標對象尺寸加大或者分散程度較高，此時就需通過擴展作業空間的方式擴大機器人的作業范圍，或者通過增加機器人的數量來完成對目標對象的加工處理。但無論是通過哪種方式完成加工，都需要對機器人的加工位置進行跟蹤控制，保證在最少的加工站位轉換次數和最小機器人數量的情況下完成加工作業。這種方式能夠在保證最高效率的前提下，減少作業成本。

為此，相關學者設計了基于布谷鳥算法的機器人移動軌跡跟蹤控制方法[2]和基于光學運動跟蹤系統的機器人末端位姿測量與誤差補償控制方法[3]，實現對機器人加工位置和軌跡的控制。但上述傳統方法在控制過程中，未針對連續加工過程中的相關控制展開研究。

為減小加工過程中機器人的位移量，本研究設計了自動化裝配機器人加工站位跟蹤控制方法，以最優加工站位為跟蹤控制目標、以保證加工質量為前提，實現加工站位和機器人數量最小化，從而最大程度地提升生產效率、降低生產成本。

1 機器人加工站位跟蹤控制

1.1 加工站位跟蹤控制優化模型

機器人參與加工制造的過程通常是連續作業。根據機器人的加工站位，采用離散化手段對其連續位姿空間實行處理，獲取離散后的一組站位W={wi}ni=1。將機器人加工站位最佳跟蹤控制問題轉換成從W中完成選擇加工站位優化的問題，定義其為優化內容【1】。從W中選取加工對象，且該對象在完成加工時的站位最控制。控制模型公式為：

式中：xi表示二值整型變量，且與wi相對應。模型的約束條件為：

式中：T表示約束集合，其屬于所有的加工對象，且T={ti}mi=1；如果F(wi)表示所有加工對象集，xi的值為1，則wi為加工站位，反之，xi的值為0，F(wi)=φ。

1.2 加工站位優化選取

在求解模型時，為避免求解規模較大，快速實現模型求解，本文分為兩個步驟完成模型求解，一是加工對象合并處理，二是加工站位跟蹤控制優化求解。

1.2.1 基于聚類算法的加工對象合并處理

用t表示加工對象，如果其在加工站位w下的加工情況符合加工要求標準，則表示t的可行加工站位是w，w的可加工對象為t，w→t。Ow和OT均表示集合，前者對應加工站位，后者對應加工對象，由此完成序偶定義：O=〈Ow，OT〉、OW≠φ、OT≠φ，則存在：w→t、?w∈OW、?t∈OT。

各個加工對象的可行加工站位的獲取，可依據加工對象的可加工性分析得出，當任一加工對象不存在可行加工站位時，則不對其實行加工。采用序偶及描述可加工性分析結果，其為M={O1，O2，...，Om}，其中加工對象用OTi表示，且OTi={ti}，i=1，2，...，m，序偶的聚類計算公式為：

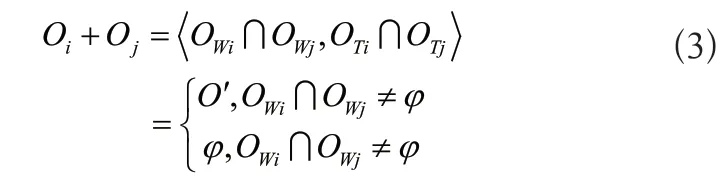
運算后，即使結果不等于φ，但是依舊存在一個有效的序偶O'。通過聚類對M中除φ以外的每兩個差異的元素均實行運算，形成集合M1。

如果M中每兩個差異的元素運算后，如果結果等于φ，則將其加入M1中，并且不進行后續運算。將M1中冗余元素去除后，對其中每兩個差異的元素均實行運算，形成集合M2，按照上述M的處理步驟實行處理，獲取M3。以此類推，當集合Mmax中只存在一個元素后者每兩個差異的元素運算后的結果等于φ時，停止運算。此時可得到：

式中：O'i=〈O'wi，O'Ti〉，i=1，2，...，m'表示序偶。

通過上述的聚類處理后，加工站位跟蹤控制優化問題可定義成優化內容【2】，其模型公式為：

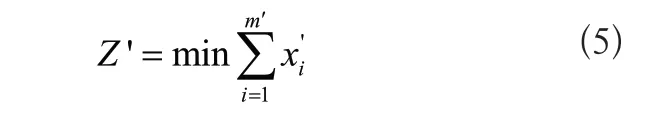
模型的約束條件公式為：

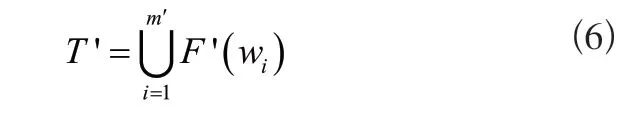
式中：xi表示二值整型變量，且與O'i相對應；如果選中O'i，那么xi的值等于1，F（wi）=O'i；xi的值等于0，F（wi）=φ。

通過上述步驟即完成聚類運算，該運算可顯著降低問題求解規模。

1.2.2 加工站位最優求解

為實現對機器人加工站位的最佳跟蹤控制，需保證控制后機器人的加工站位為最佳，本研究采用遺傳算法對模型進行求解，從而獲取最佳加工站位。

首先對機器人的加工順序實行規劃，將其轉換成旅行商旅問題，定義出發點為機器人的初始位姿，完成機器人的所有視點的遍歷[4]，且不重復，最終返回到初始位置，X表示搜索自然子集，且X={1，2，...，n}，其中每個元素均用于描述視點的編號，X的排列則為n(X)，且n(X)={V1，V2，...VN}，使，并且取其結果最小值，其中d(Vi，Vi+1)表示距離，屬于兩個視點之間，即Vi和Vi+1。

基于遺傳算法的求解步驟如下所述：

1）采用編碼的方式對數量為n的視點實行描述，且該視點屬于機器人固定站位工作范圍內。

2）定義數量為N的個體為種群，通過初始化對其實行處理。

3）構建適應度函數模型：

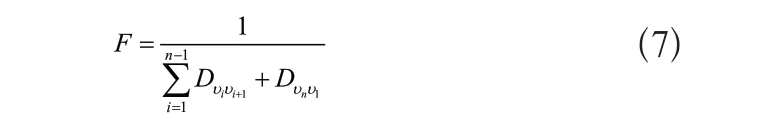
式中：vi表示染色體，且為整數編碼；Dvnv1表示歐幾里得距離，屬于兩個視點之間，即vi和vj。

4）對個體實行選擇，將概率P作為選擇標準，將選擇的個體加入新種群中。

5）采用交叉、變異、進化以及逆轉的操作對種群實行處理。

6）重復上述操作，如果達到設定最大迭代次數，則停止迭代，輸出求解的最佳的加工站位；反之，則返回步驟3，從新迭代，直到滿足條件為止。

1.3 軌跡補償

通過上述內容能夠確定自動化裝配機器人的最優站位，但是機器人在加工過程中，會受到反作用力和力矩的影響，使機器人的站位發生影響和變化，該變化經過累積后，導致最終加工的精度受到影響。因此，本文為了更好地實現機器人加工站位的控制，采用軌跡補償方法對其實行處理。該方法是通過構建機器人振動模型，以機器人加工過程中產生的反作用力作為外界激勵，得出機器人在加工過程中發生的位移響應；并計算位移曲線和理論加工軌跡之間的差，以此獲取機器人的軌跡[5]，并將該軌跡作為控制指令，用于實現機器人的控制，實現機器人在加工過程中的抗干擾性能。

機器人的質量、剛度、阻尼分別m、k、c，其自由變量為y、、，機器人發生的位移、速度和加速度可通過三個自由變量描述。以牛頓定律為依據，得出振動微分方程，其公式為：

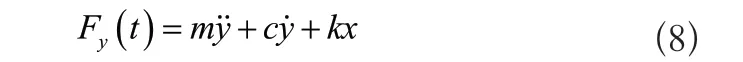
式中：Fy(t)表示激振力函數，其產生在受到外界影響的情況。式(8)是一個非齊次線性方程，齊次解y1(t)、非齊次解y2(t)均是該方程的最終解。

在Fy(t)=0的情況下，獲取方程的零輸入相應結果，并通過拉普拉斯對其實行轉換后得出：

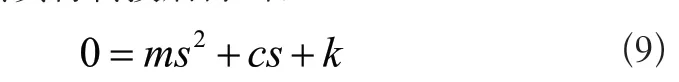
以二元一次方程的求根公式為依據得出：

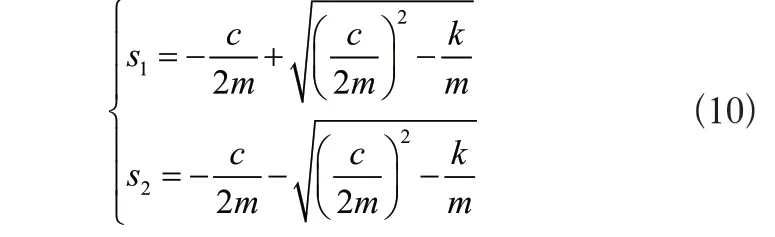
式(10)的兩個解的線性組合即為式(9)的方程解，則采用式(11)表示零輸入響應的解：

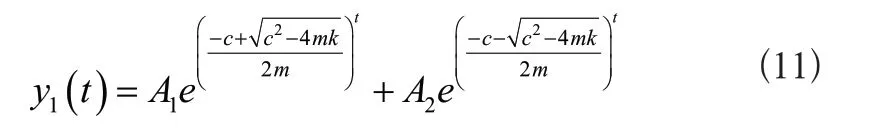
式中：待定系數用A1、A2表示。

如果存在下式關系：

式中：ξ表示阻尼比。此時式(9)可轉換為：

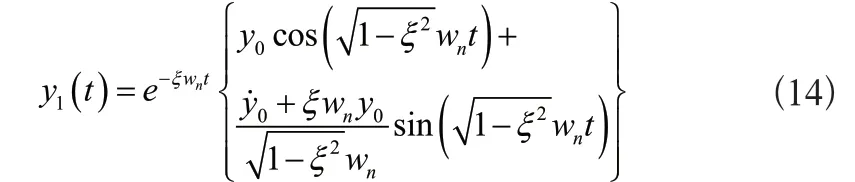
式中：y0和分別表示機器人的初始位移和速度。假設δ(t)表示沖擊函數，疊加δ(t)可用于描述連續函數，因此在求解振動位移響應前，需計算沖擊響應，結合動量定理得到：

如果0+和0-均屬于時刻，前者對應沖擊作用前，后者對沖擊作用后，那么0-時的位移和速度為y(0-)=y(0.-)=0。采用積分的方式對式(15)實行積分得出：

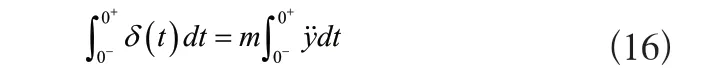
對式(16)實行化簡，其依據性質和定理完成，且分別對應沖擊函數和積分，化簡后公式為：

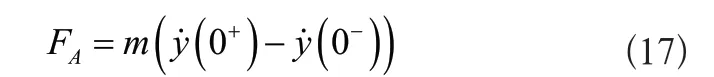
式中：幅值為FA，屬于沖擊力。基于此得出：

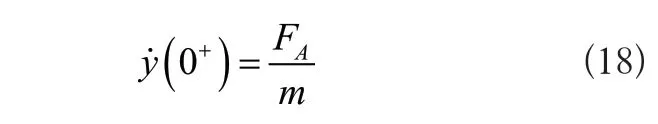
基于式(18)可知機器人在受到沖擊時，只有速度發生變化，則機器人在靜止狀態下，受到沖擊作用的初始條件為y（t=0），（t=0）=1/m。將其代入式(14)得出：

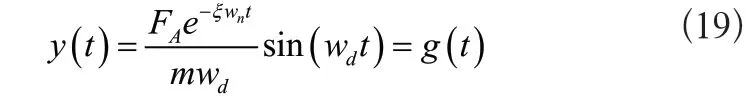
式中：wd表示頻率，屬于阻尼且為固有；g（t）表示沖擊位移響應，屬于機器人。

如果瞬間沖擊力在任意的t-τ時刻導致的瞬時速度均用FA/m表示，則可采用沖擊響應g(t-τ)的疊加描述連續函數F(t)，在Δτ→0的情況下，將該疊加轉換成積分[6]。

由于在實際加工時，無法通過準確的一個函數實現激振力函數的描述，因此，需求解積分，其通過數值解法完成。如果實際激振力函數曲線通過階躍函數逼近，則階躍值在t=t1=0時刻的大小為ΔF1，在已有的i組離散力和其對應時刻數據的情況下，可得出離散力數據的激勵響應：

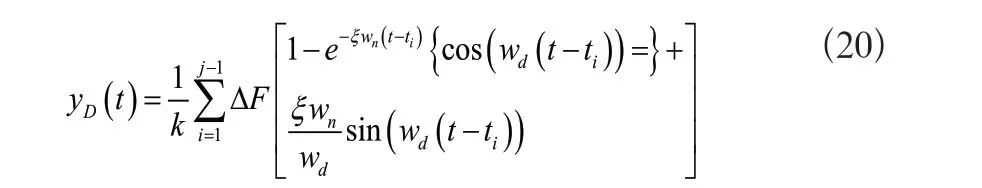
獲取激勵響應后，采用五次多項式加工站位軌跡補償，實現機器人站位的穩定控制，有效避免加工過程中的干擾。

2 測試分析

為測試上述設計的自動化裝配機器人加工站位跟蹤控制方法的應用效果，將其用于某壓鑄加工現場展開實際測試。該加工現場待壓鑄加工對象數量16個，每一個壓鑄對象之間的距離為2m，兩面待壓鑄對象之間的距離為5m，機器人加工站位范圍位于兩面待壓鑄對象中間位置，詳細分布情況用圖1描述。

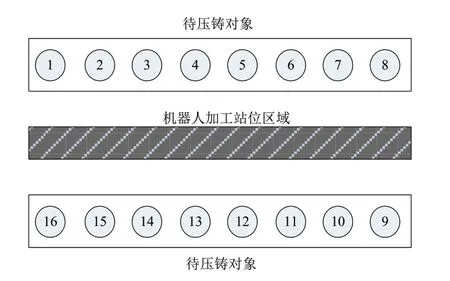
圖1 自動化加工現場

圖1中，自動化裝配機器人型號為LAT-3500，其工位最大半徑為3.5m，工作溫度為0～45℃，動作自由度4，最大負載能力25kg，重復定位精度為±1.5mm，工作范圍X軸330°，Y軸3.1m，Z軸2.05m～2.25m。應用期望標準為只使用一臺機器人，在最少站位下實現16個加工對象的壓鑄，并且保證壓鑄質量，且壓鑄過程中，機器人發生的位移在10cm以內。

在使用本文方法實行加工站位跟蹤控制前，需設定本文方法的最大迭代次數，以加工視點之間的歐幾里得距離的收斂情況作為確定標準，獲取文本方法在不同迭代次數下，該距離的收斂情況，結果用圖2描述。

對圖2的測試結果實行分析得出：本文方法隨著迭代次數的增加，歐幾里得距離逐漸收斂，當迭代次數達到100次以后，距離達到最小值并且不再發生變化，處于平穩狀態。因此，本文方法的最大迭代次數為100次。

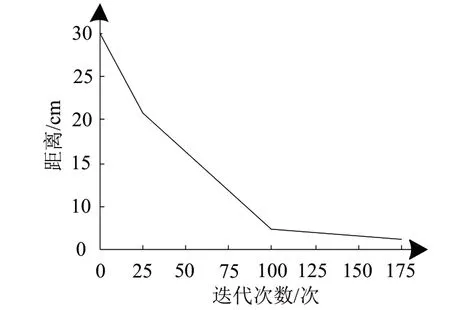
圖2 迭代次數測試結果

為測試本文方法的加工站位最優跟蹤選取效果，依據應用期望標準，對加工現場的站位實行選取確定，獲取本文方法選取的加工站位結果，用圖3描述。

圖3 加工站位選取結果

對圖3的測試結果實行分析得出：本文方法在應用期望標準下，能夠完成機器人加工現場的站位選取，共確定3個加工站位，能夠實現所有加工對象的壓鑄加工。因此，本文方法具備機器人加工站位優化跟蹤能力，能夠確定最佳加工站位位置。

為測試本文方法在機器人加工過程中，對于機器人站位位移的控制效果，獲取機器人距離加工對象不同距離時，實際壓鑄接觸著力點與目標著力點的吻合程度，結果用圖4描述。

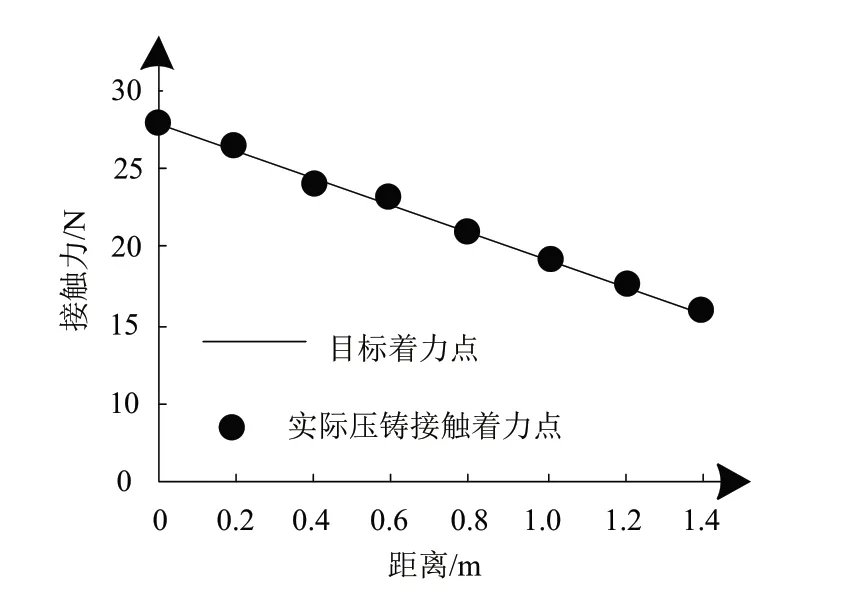
圖4 站位位移測試結果

對圖4的測試結果實行分析得出：隨著機器人和加工對象之間距離的逐漸增加，實際壓鑄接觸著力與目標著力點的吻合程度較高，沒有發生明顯偏離情況，是由本文方法具備軌跡補償功能，能夠有效控制加工過程的反作用力，因此能夠保證良好的站位控制效果，同時實現著力點的吻合。

為分析本文方法的跟蹤控制效果，測試本文方法在機器人不同位姿角度下，隨著反作用力的增加，機器人發生的位移結果用圖5描述。

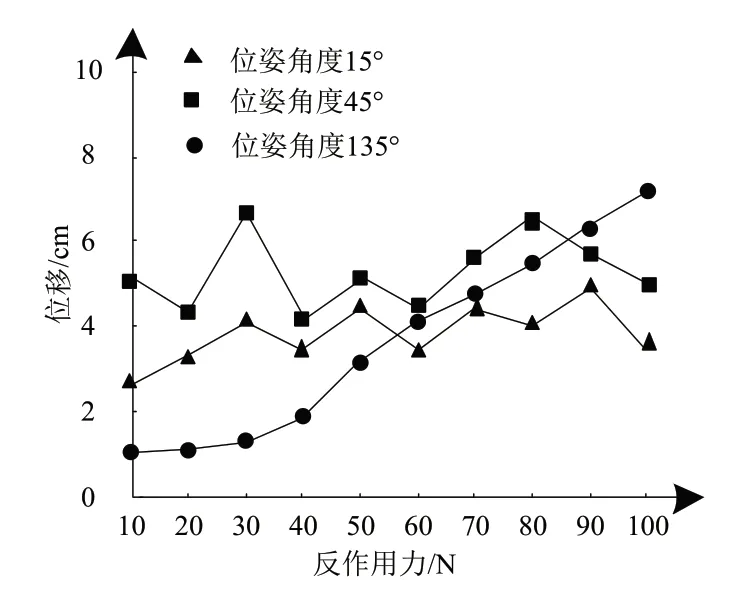
圖5 機器人位移測試結果

對圖5的測試結果實行分析得出：在不同的位姿角度下，隨著反作用力的逐漸增加，機器人發生不同的位移結果；其中位姿角度較小時，位移呈現不規則的波動變化，當位姿角度較大時，位移呈現逐漸上升趨勢。但是位移的結果均在10cm以內，符合應用期望標準。

3 結語

自動化裝配機器人在加工過程中的站位與加工效率和生產成本之間存在直接關聯。為實現生產成本最小化，加工對象的最大覆蓋程度，并且在最小站位數量下實現高精度的加工作業，本文研究了自動化裝配機器人加工站位跟蹤控制方法。該方法能夠獲取最優的加工站位結果，同時能夠最大程度避免加工反作用力的干擾，保證機器人加工時的位移最小化，保證機器人的加工穩定性。