SCARA機器人控制系統的設計與實現

李 宏，陳 平，劉宋彬

（廣東工業大學 自動化學院，廣州 510006）

0 引言

SCARA（Selective Compliance Assembly Robot Arm）即選擇順應性裝配機械手，是一種圓柱坐標型的工業機器人，該機器人具有三個自由度，分別負責伸縮、旋轉和升降運動[1]。主要應用于電子制造行業，比如IC點焊、元件貼片、貨品分揀等制造當中[2]。

對SCARA機器人開展的研究集中在1）基于運動學、動力學進行數學建模分析，研究機械手軌跡規劃的新方法[2～4]；2）引入新的設計方法優化機器人的控制算法，提高可靠性，抗干擾能力以及性能指標[5～7]；3）研究機器人與視覺相結合的新方法，不斷優化控制精度和運動指標[1，8～9]；4）研究機器人標定的新方法，提高定標的精度和降低設計的復雜度[10，11]等。

1 SCARA機器人的運動學分析

SCARA機器人是一種平面關節機器人，具有三個旋轉關節和一個垂直于平面的移動關節，其D-H參數坐標系如圖1所示。其中坐標系{O0}為工作坐標系，原點O0的坐標為(0,0,0)。{O1}，{O2}，{O3}為流動坐標系，{O4}為工具坐標系。{O4}代表機器人末端執行器的位姿。參數變量θ1為機器人大臂關節角度變量，θ2為小臂關節角度變量，d3為手腕關節平移變量（d3由電機角度變量θ3通過轉換得到），θ4為末端執行器的關節角度變量。連桿參數為ai=ai=li，i=1，2，3。

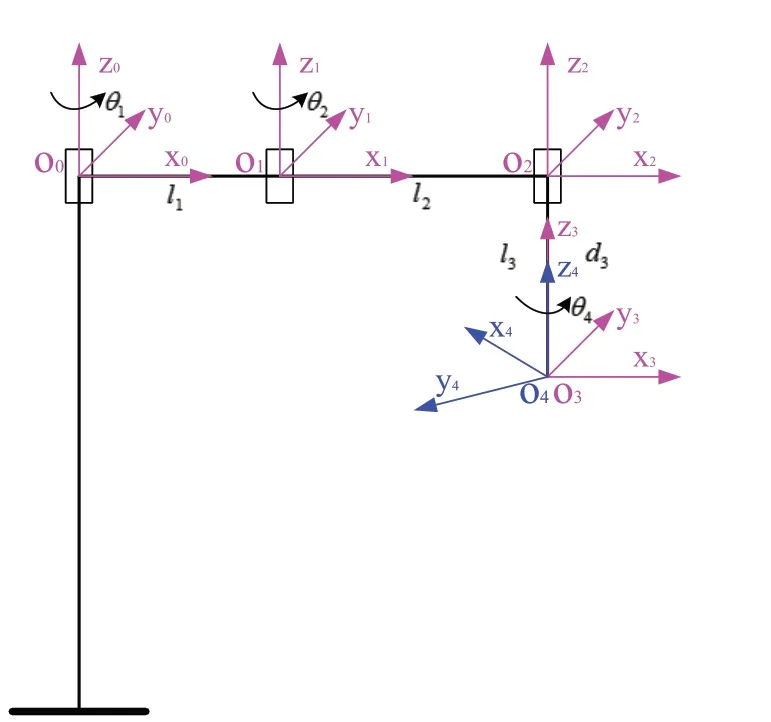
圖1 SCARA機器人D-H參數坐標

根據矩陣變換原理及圖1 SCARA機器人的結構特點，給出SCARA機器人工具坐標系與工作坐標系之間的齊次變換矩陣為

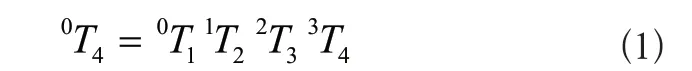
其中iTi+1，i=0，1，2，3表示坐標系{Oi+1}相對于坐標系{Oi}的位姿，其表達式分別為

其中Rot（z，θ）操作表示坐標系{Oi+1}沿坐標系{Oi}的z軸旋轉θ角度，Trans（x，d）操作表示坐標系{Oi+1}沿坐標系{Oi}的x軸平移d距離，因此可得工具坐標系{O4}相對于工作坐標系{O0}的位姿矩陣為

由式(2)可得機器人末端夾具的直角空間位姿與關節角度變量的變換關系，因此可得機器人正運動學解為

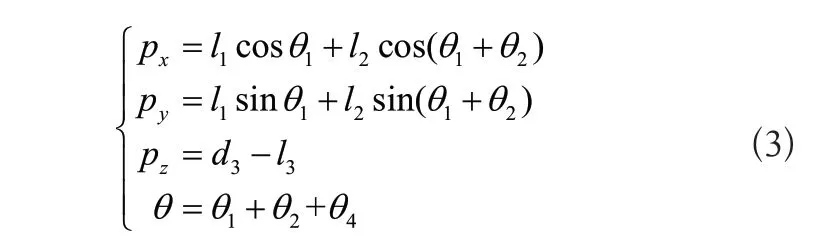
其中坐標點(p x,p y,pz)為{O4}的原點相對于{O0}的空間坐標，θ為{O4}相對于{O0}的姿態。根據式(1)推導SCARA機器人反運動學解，將式(1)變換為：

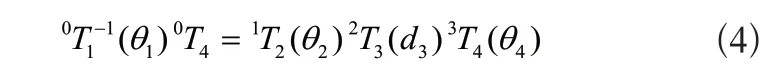
分別代入iTi+1，i=0，1，2，3的表達式，可得

在文章中，我們提出了一個安全的、可擴展的電子數據存證系統，該系統采用數據與用戶對應映射關系查找來確保對電子數據池的高效訪問控制。我們設計了一個基于區塊鏈的數據存證方案，允許數據用戶/所有者在身份驗證后，從電子存儲庫訪問電子數據。數據存儲主要進行分片冗余算法和分布式存儲保證數據安全性，并且系統引入用戶積分機制，保證系統負載均衡。驗證和后續服務封閉在系統內部，寫入區塊并成為區塊鏈的一部分。

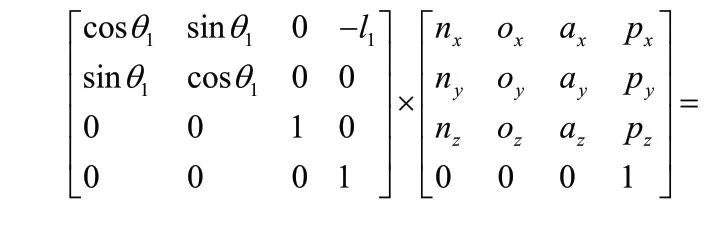
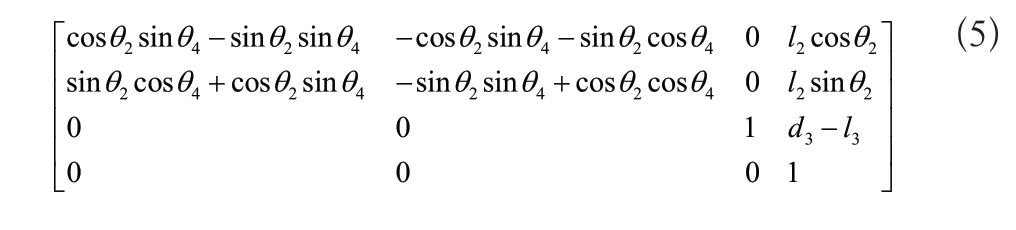
將式(5)等號兩邊矩陣元素一一對應，選擇矩陣元素(1，4)和(2，4)聯立方程組為

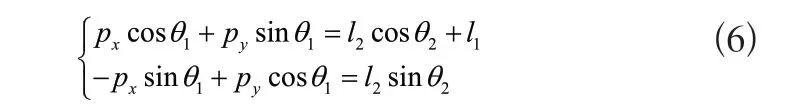
由式(6)推導可得反運動學解為

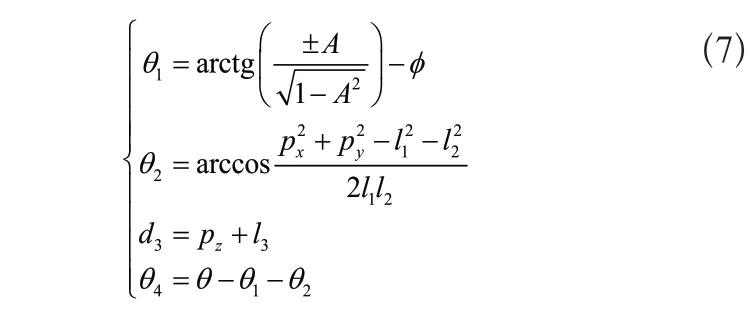
其中變量A和φ分別為

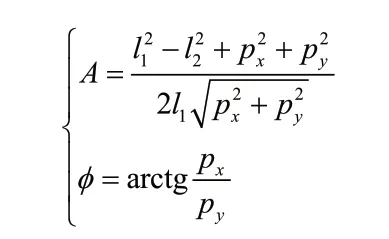
D-H參數坐標的建立，以及正反運動學的分析為SCARA機器人建立起基本的數學模型，為控制系統的算法設計提供理論基礎

2 控制算法的設計與仿真

SCARA機器人一般實現兩點之間的運動，根據運動形式具有點對點運動，即兩點之間運動軌跡為任意曲線；另一種為直線運動，是點對點運動的特殊形式，通過插補方法可實現兩點之間的直線運動。為了驅動SCARA機器人運動，將目標點位姿信息作為輸入指令，控制算法根據輸入指令計算得到的關節角度及角速度作為控制量輸出。為了改善機器人工作指標，可選擇增加路徑規劃算法。基于工控機+分布式控制架構的機器人控制原理如圖2所示。

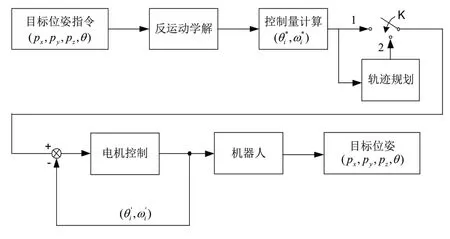
圖2 SCARA機器人的基本控制原理

圖2中，（px，py，pz）表示目標點的空間位置，θ表示工具坐標的姿態，輸出的控制量θ*i，i=1，2，3，4表示目標位姿的四個關節角度，控制量ω*i表示四個關節的角速度，（θ'i，ω'i）分別表示四個關節角度和角速度的反饋信息，實現電機的位置和速度閉環控制。角速度計算表達式為，i=1，2，3，4，其中T為起止兩點之間的運動時間，θ0i為初始位姿下的四個關節角度。

根據以上分析，在MATLAB Robotics Toolbox工具中對SCARA控制系統進行建模仿真，首先根據機器人樣機參數及D-H參數法建立SCARA機器人數學模型，如表1所示。

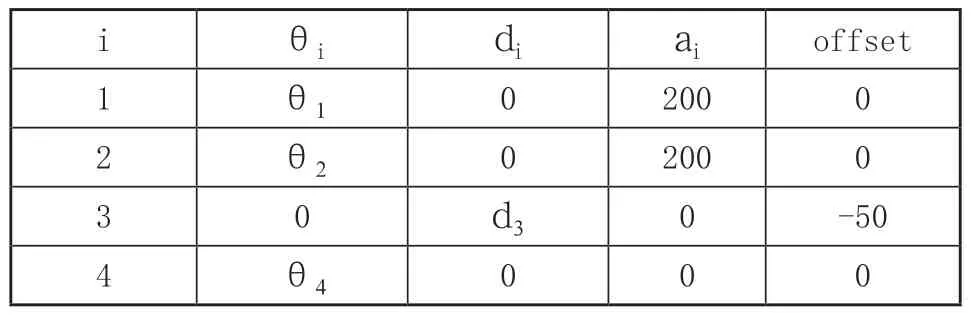
表1 SCARA機器人D-H參數表

表中i表示關節編號，θi表示變關節角度變量，ai為關節之間的連桿參數變量，大臂與小臂的連桿長度均為200mm，offset表示工具坐標{O4}原點在初始狀態下的偏移量，由表1可知初始狀態下{O4}的原點相對于{O0}的坐標為（0，0，-50）。SCARA機器人數學模型的程序代碼如下：

其次，根據圖2控制算法原理、表1的D-H參數表和式(7)設計SCARA機器人控制算法，當輸入的任意空間位姿信息在機器人工作范圍內，機器人能夠準確到達指定位置。比如在初始位姿(400，0，-50，0)下，輸入目標位姿指令(300，0，-20，45)，得到仿真結果如圖3所示。

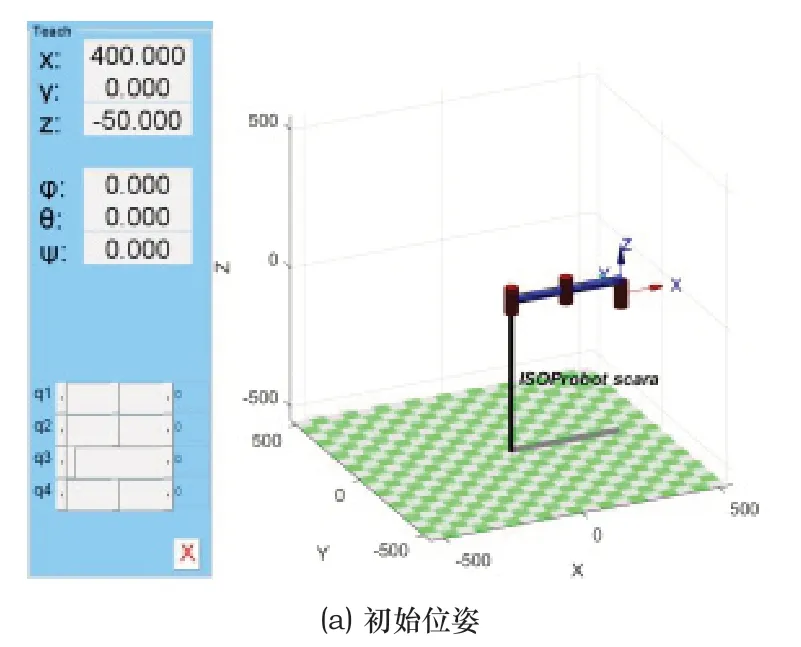
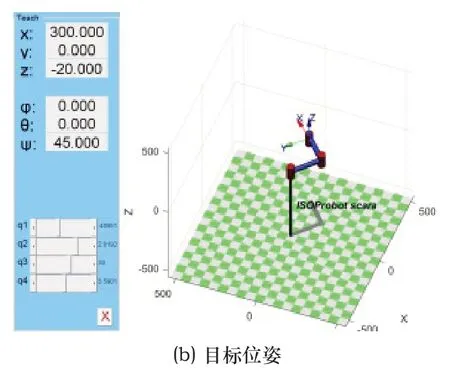
圖3 機器人仿真結果

圖3中，（X，Y，Z，Ψ）顯示機器人的位姿信息，仿真結果表明機器人能夠按照輸入指令準確到達目標位姿，初步證明控制算法的可行性。

3 SCARA機器人控制系統的設計

SCARA機器人硬件平臺采用工控機+分布式控制的架構，其架構原理圖如圖4所示。其中工控機完成運動學解、路徑規劃、電機信息采集，控制量輸出，串口通信以及人機界面等功能；CAN站點表示驅動SCARA機器人關節的步進電機系統，步進電機系統集控制，驅動和電機本體為一體，站點之間獨立工作，分別接受工控機指令并獨立完成驅控操作。

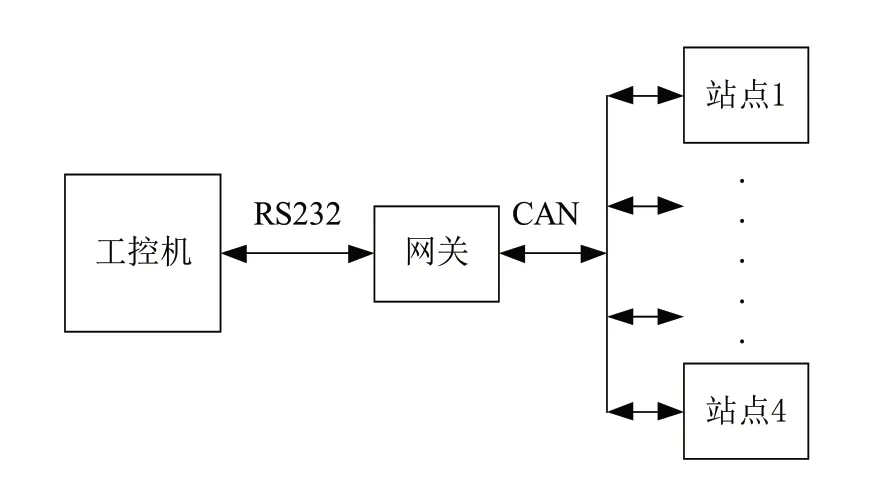
圖4 SCARA機器人硬件平臺架構

SCARA機器人直線運動一般采用插補方法，在初始位姿（p0x，p0y，p0z，θ0）和目標位姿（p*x，p*y，p*z，θ*）之間根據要求平均插入n個插補點，可得每個插補點之間的步增距為

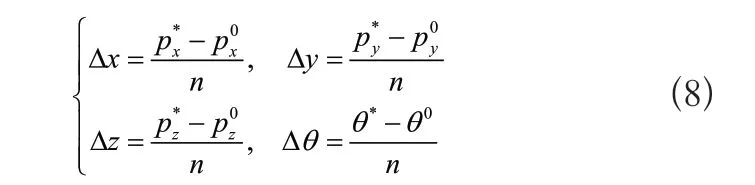
則第j個插補點的位姿為為

然而由于實際信道存在通信延遲，四個站點在接收指令時存在時間差，因此影響直線運動的精度。為了修正該精度誤差，應將通信延遲時間納入角速度的計算之中。假設指令傳輸延遲時間為σ，則按順序站點1至站點4的通信延遲時間為λi=σ×i，i=1，2，3，4。則兩個插補點之間的角速度應修正為。經過修正之后機器人能夠精確經過每一個插補點，實現直線運動。機器人控制系統的軟件流程圖如圖5所示。

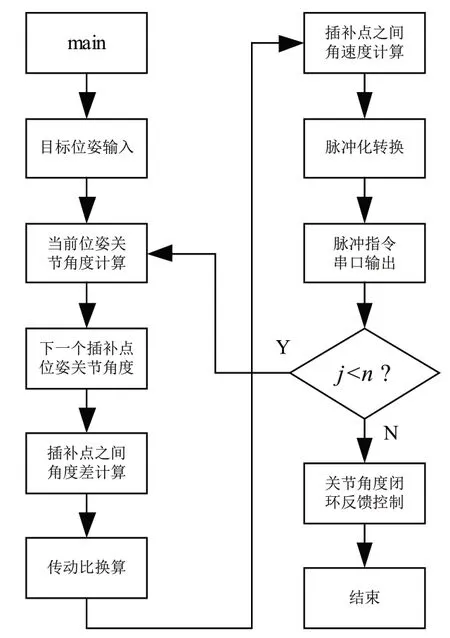
圖5 SCARA機器人直線運動控制的軟件流程圖

在直線運動過程中，控制系統循環計算兩個插補點之間的角速度，并且在下一個插補周期開始時刻更新四個關節的角速度，使得機器人能夠精確經過每一個插補點位置。圖5中，傳動比轉換模塊將機械關節角度轉換為電機的旋轉角度；脈沖化轉換模塊將電機角速度轉換為脈沖指令；關節角度閉環反饋控制模塊將精確控制機器人準確到達目標位姿上。通過以上軟件流程實現機器人直線運動控制。

4 實驗測試

搭建SCARA機器人控制系統，包括：PC，USB/CAN轉換器以及SCARA機器人。在PC上安裝LabVIEW軟件工具，利用LabVIEW設計控制算法。USB/CAN轉換器連接PC以及SCARA機器人四個關節電機。四個關節電機均為步進電機驅控一體機，該系統集控制，驅動和電機本體為一體，步進電機系統之間相互獨立，分別接受上位機的指令并驅動步進電機工作。SCARA機器人控制系統如圖6所示。

圖6 SCARA機器人控制系統實物圖

在LabVIEW中設計SCARA機器人控制算法，并提供人機界面供用戶輸入目標位姿指令。SCARA控制系統的LabVIEW程序及人機界面如圖7所示。

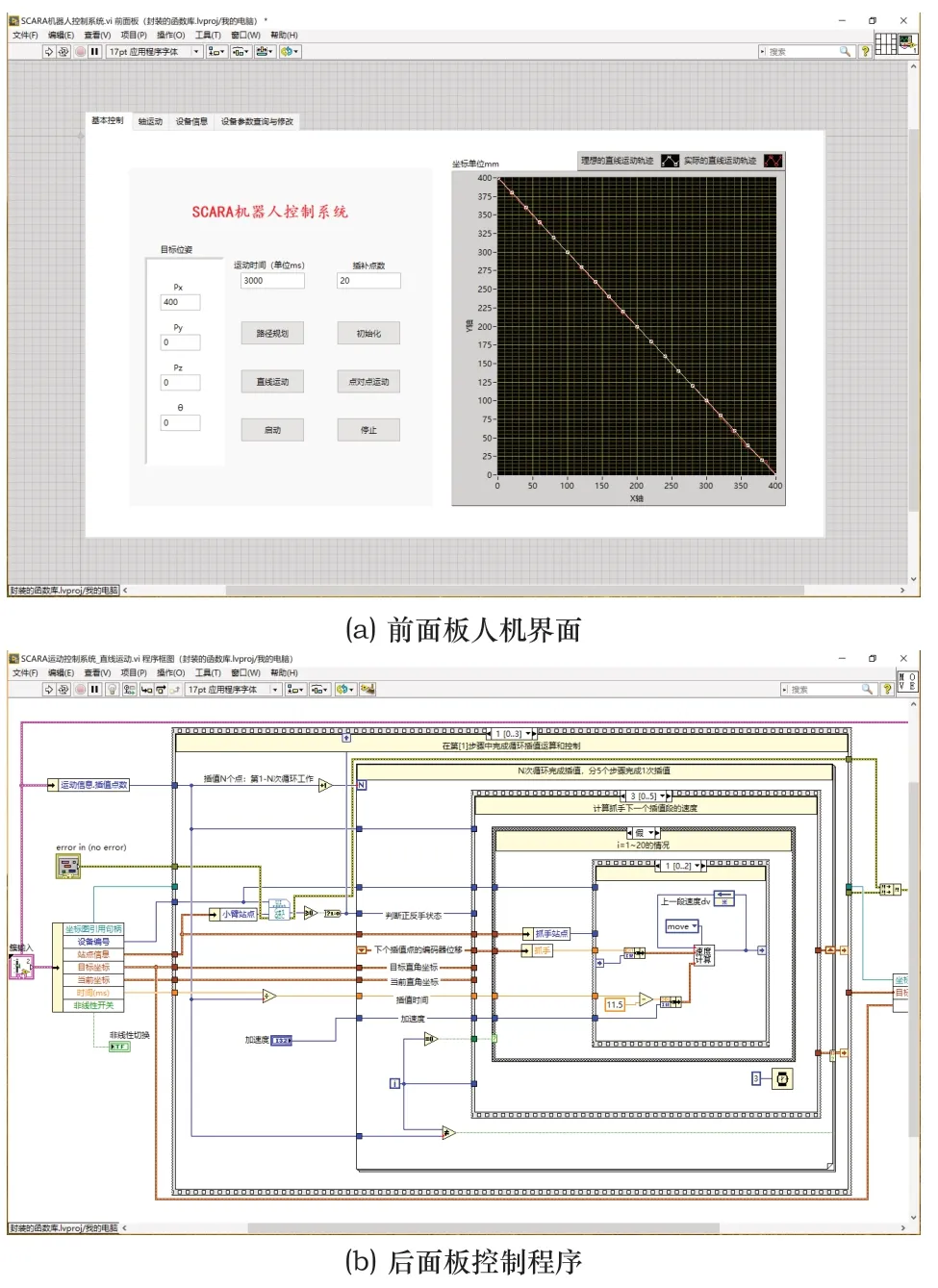
圖7 SCARA機器人控制算法的軟件設計圖

圖8中，x-y平面表示SCARA的工作平面，由圖8(a)和(b)的結果對比可知，通信延遲誤差修正方法能夠有效解決工控機+分布式控制架構下直線運動的精度問題。圖8(c)為增加軌跡規劃算法，采用非線性插補方法之后得到的實驗測試結果，同樣具有良好的控制精度。軌跡規劃算法使得機器人在啟動和停止階段具有更平滑的運動軌跡，有利于機器人的精度和穩定性。

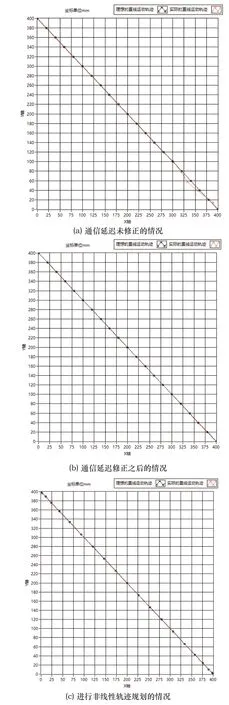
圖8 SCARA機器人直線運動軌跡圖

5 結語

本文主要探討了基于工控機+分布式控制架構下SCARA機器人控制系統的設計與實現等問題。闡述了數學建模，控制算法設計，軟件仿真以及硬件實現的一般過程及設計方法，實驗結果表明該方法的有效性和實用性。本文的工作為下階段的研究工作提供理論基礎及技術框架。基于現有的工作基礎，可進一步改善系統的性能指標，及拓展其技術內涵。