基于LSTM的軌道電路補償電容故障數量預測

康玄燁，趙林海，孟景輝，高利民

(1. 北京交通大學 電子信息工程學院，北京 100044； 2. 中國鐵道科學研究院集團有限公司 基礎設施檢測研究所，北京 100081； 3. 中國鐵道科學研究院集團有限公司 鐵路基礎設施檢測中心，北京 100081)

無絕緣軌道電路在我國高速鐵路列車運行控制系統中占有非常重要的地位，其主要被用來檢測列車占用和實現地-車間通信，以保障行車安全[1]。補償電容作為無絕緣軌道電路的組成部分，主要用來改善信號在軌道線路中的傳輸性能[1]。由于補償電容安裝在室外，受外部環境和列車運行的影響較大，故障率相對較高[2]，因此需要相應的運維部門提前準備好足量的備品以備更換。某電務段2017年1—12月所管轄范圍內補償電容的故障情況見圖1。

圖1 某電務段2017年1—12月補償電容的故障情況

由圖1可知，每月的補償電容故障數并不相同，存在較大的波動。而由現場調研得知，補償電容預備品數目是固定的，這往往會導致兩種情況：一種是備品不夠造成維修不及時；另一種是備品過多造成資源浪費，占用存貯空間。若能夠準確預測近期內所轄范圍內補償電容的故障數量，則可更有效地準備備品，節約維修成本，合理安排維修計劃。

近年來，隨著我國鐵路網的進一步發展，鐵路基礎設備不斷增多，越來越多的研究者開始關注鐵路設備的故障預測[3-5]。然而，國內外還沒有補償電容故障數量預測研究的相關報導。與此相關的只有文獻[6]，其基于相空間重構Kalman濾波求解單個補償電容的剩余壽命，實現的是對單個補償電容容值下降的故障預測。

本文基于鐵路現場補償電容的故障記錄，構建補償電容故障數量的時間序列，利用長短時記憶(Long Short-Term Memory，LSTM)設計故障數量預測模型，針對LSTM初始化超參數對預測模型性能有較大影響的問題，利用螢火蟲算法對超參數進行優化，從而挖掘補償電容故障數量隨時間的變化規律，并實現對補償電容故障數量的預測。實驗表明，本文方法能較準確地預測補償電容故障數量，誤差相對較低，從而可以幫助鐵路維護部門提前協調設備、資金和維修人員等資源，為補償電容的運維提供良好指導。

1 整體思路

通常，鐵路現場補償電容故障歷史記錄中含有故障日期、故障位置和故障發生區段所屬車站等信息。根據這些記錄可構建補償電容的故障數量時間序列，以挖掘該序列隨時間的變化規律，從而實現對補償電容故障數量的預測。考慮到現場是按一定的時間間隔和維修計劃對補償電容進行批量維護[7]，故本文以“15天”為單位，即令時間間隔T=15，所構建補償電容故障數量時間序列X為

(1)

式中：x(i)為補償電容第i個時間間隔內的故障數量；xD(t)為補償電容第t天的故障數量。

由于時間序列前后數據之間具有較強的依賴關系，而LSTM具備前饋神經網絡不存在的橫向連接，上一時刻隱含層的輸出作為當前時刻隱含層輸入的一部分，這種連接方式使其能夠有效處理數據前后的依賴關系，并揭示數據間的長期依賴性[8]，故本文基于LSTM構建預測模型，并利用螢火蟲算法優化模型的超參數，從而實現對補償電容故障數量的預測。基于LSTM的補償電容故障數量預測算法框圖見圖2，主要包括LSTM預測模型構建和模型優化兩部分。

圖2 基于LSTM的補償電容故障數量預測算法框圖

由圖2可知，LSTM預測模型構建部分主要包括：輸入層、隱含層、輸出層和網絡訓練4個環節。輸入層根據初始化超參數將數量序列轉換為與LSTM相適應的輸入；隱含層是由LSTM構成的神經網絡；輸出層根據LSTM的輸出計算補償電容故障數量的預測值；網絡訓練根據預測值與實際值之間的損失更新隱含層和輸出層的參數。模型優化部分利用螢火蟲算法搜索預測模型最優的超參數，從而確定最優的預測模型，得到相應的補償電容故障數量預測結果。

2 LSTM預測模型構建

2.1 預測模型框架

基于LSTM的預測模型框架見圖3，其中：輸入層對補償電容故障數量序列進行預處理，并構建數據集；隱含層是LSTM的循環運算過程；在輸出層中，加權平均層是對每一時刻LSTM的輸出進行加權求和，Dropout用于提高網絡泛化能力和健壯性[9]，預測層計算預測結果；網絡訓練部分根據實際值與預測值之間的誤差，利用AdaDelta算法[10]更新網絡參數。

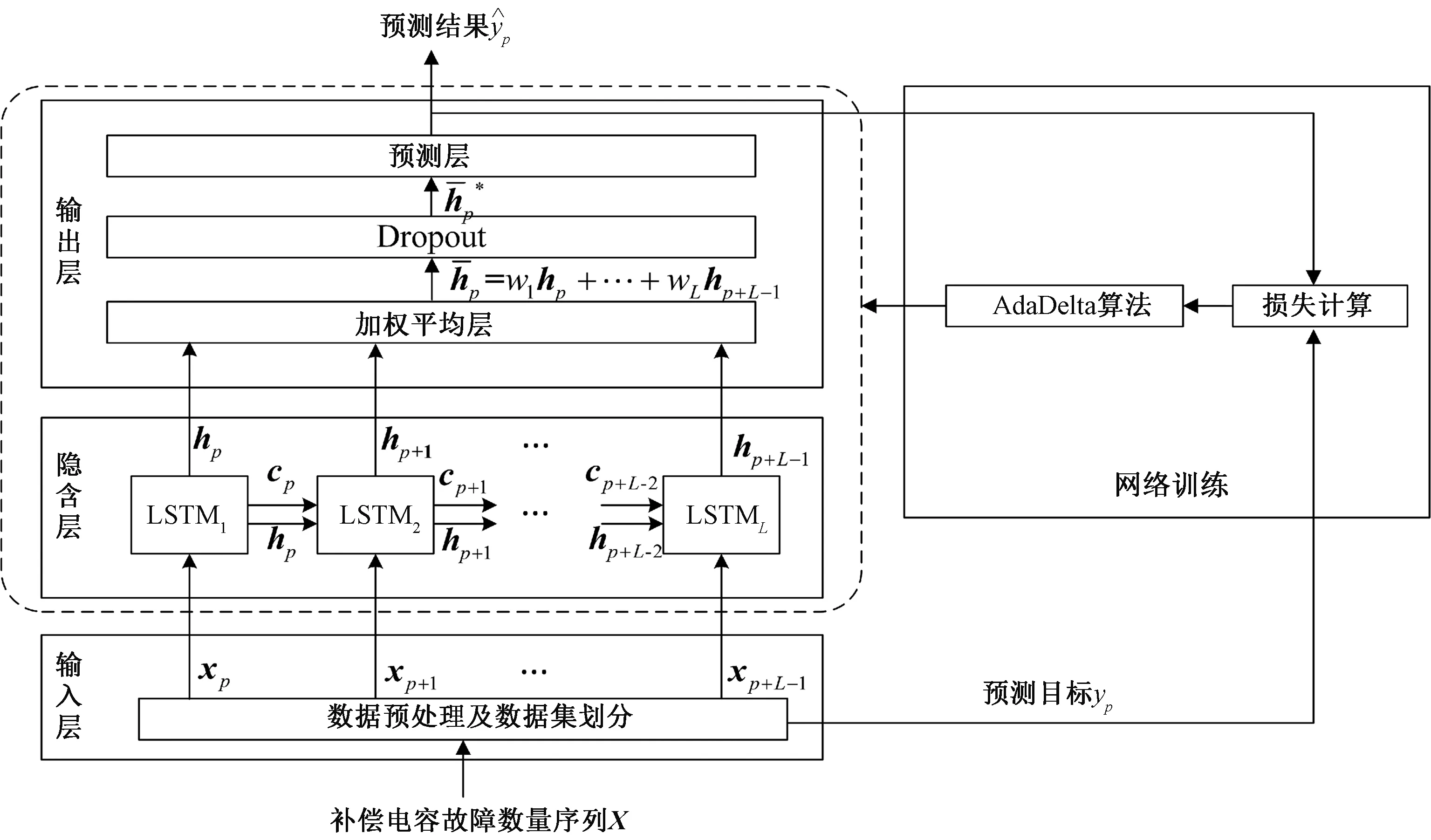
圖3 基于LSTM的預測模型框架

2.2 輸入層

設LSTM循環次數為L，序列分割窗口長度為m，由式(2)將數量序列X={x(i)|i=1，2，…,n}轉換為LSTM的輸入特征矩陣Xp及其對應的預測目標yp。

(2)

從而構建補償電容故障數量的數據集{XB,Y}為

(3)

得到數據集{XB,Y}后，將其劃分為訓練集{Xtr,Ytr}、驗證集{Xva,Yva}和測試集{Xte,Yte}，為預測模型的訓練和驗證提供數據支持。

2.3 隱含層

LSTM的結構見圖4，主要包括：信息激活、細胞單元、輸入門、輸出門和遺忘門等5部分。

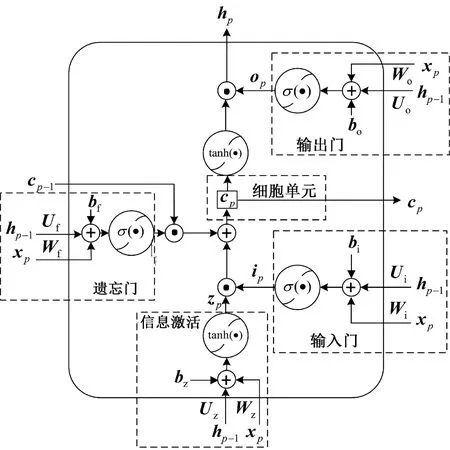
圖4 LSTM的結構

圖4中：hp-1和xp分別為p-1時刻和p時刻LSTM的輸出和外部輸入；在輸入門、輸出門和遺忘門中，hp-1和xp分別與各門對應權值矩陣Ui、Uo、Uf和Wi、Wo、Wf相乘，再與對應的偏置向量bi、bo、bf相加后，經激活函數σ(·)得到各門p時刻輸出結果ip,op,fp；信息激活過程中，hp-1和xp分別與對應權值矩陣Uz和Wz相乘，再與對應的偏置向量bz相加后，經激活函數tanh(·)得到p時刻輸出結果zp；p-1時刻細胞單元cp-1與遺忘門的輸出fp點乘，再與ip和zp點乘的結果相加，得到p時刻細胞單元cp；cp經激活函數tanh(·)后，再與輸出門的輸出op點乘得到p時刻LSTM的輸出hp。上述過程可描述為

(4)

式中：⊙為點乘運算；σ(·)為sigmoid函數；tanh(·)為雙曲正切函數。

2.4 輸出層

輸出層包括：加權平均層、Dropout和預測層3部分。考慮到時間序列前后依賴關系的強弱，為了更充分地描述各時刻LSTM輸出對預測結果的影響，對各時刻LSTM的輸出進行加權求和，即

(5)

(6)

再經過預測層得到預測結果為

(7)

式中：I為服從P=0.5，0-1分布的隨機向量；Wy為預測層的權重矩陣；by為預測層的偏置向量。

2.5 網絡訓練

(8)

(9)

由AdaDelta算法得到參數θt的更新公式為

(10)

根據式(8)～式(10)更新預測模型中隱含層和輸出層的參數，滿足停止條件后，終止模型的訓練過程，得到完成訓練后的預測模型。

3 模型優化

預測模型需要設置的初始化超參數包括：LSTM循環次數L、窗口長度m和神經元個數r。將訓練完成的模型記作：LSTM(L,m,r)。由于不同的超參數組合(L,m,r)對模型能夠達到的預測精度有較大的影響，為了使模型預測結果達到最優，故利用基于權重的螢火蟲算法[11]搜索超參數的最優組合。

3.1 算法流程

在螢火蟲群優化算法中，螢火蟲不分性別，每只螢火蟲被視為解空間的一個解，螢火蟲種群作為初始解隨機地分布在搜索空間中，它將會被其他比它更亮的螢火蟲吸引；螢火蟲的吸引力與亮度成正比，對于任何兩只螢火蟲，其中一只會向著比它更亮的另一只移動，亮度隨著距離的增加而減少；如果沒有找到一個比給定的螢火蟲更亮，它會隨機移動，最終螢火蟲聚集到亮度高的螢火蟲周圍。螢火蟲算法優化預測模型超參數的流程見圖5，主要包括：螢火蟲初始化、模型構建、目標函數計算、螢火蟲位置更新和最優模型確定等5個環節。

圖5 螢火蟲算法優化預測模型超參數的流程

3.2 螢火蟲初始化

將LSTM循環次數L、窗口長度m和神經元個數r的組合(L,m,r)定義為螢火蟲的三維搜索空間，設各超參數的取值范圍為

(11)

式中：Z+為正整數集；Lmin,mmin,rmin為取值下限；Lmax,mmax,rmax為取值上限。

設螢火蟲數量為M，第i只螢火蟲的空間位置為Ai=(Li,mi,ri)；光強吸收系數為γ，最大吸引度為β0，步長因子為α；最大、最小權重為wmax,wmin，最大更新代數為Smax。

將螢火蟲隨機分布于三維空間，并設第i只螢火蟲與第j只螢火蟲之間的距離dij為歐式距離，即

3.3 模型構建

根據第2節預測模型構建，每一只螢火蟲都可構建出與其所處空間位置相對應的預測模型，通過網絡訓練過程，將第i只螢火蟲對應訓練完成的預測模型記作：LSTM(Li,mi,ri)。

3.4 目標函數計算

由于預測模型訓練過程中是以均方誤差作為損失函數，若螢火蟲算法依然以均方誤差作為目標函數，可能導致預測結果偏向均方誤差小的方向，不利于模型預測性能。在保證模型泛化能力的同時，為使得預測結果在平均絕對誤差與均方誤差之間達到相對最優，故以驗證集{Xva,Yva}的平均絕對誤差最小作為螢火蟲算法的目標函數。

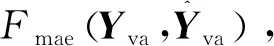
3.5 螢火蟲位置更新

螢火蟲向著熒光亮度比自身高的螢火蟲所在方向移動，它們之間的吸引度決定了螢火蟲的移動步長。螢火蟲i,j之間的吸引度為

β=β0×e-γdij2

(14)

由式(14)可進一步得到螢火蟲的位置更新公式為

(15)

式中：R為[0,1]上服從均勻分布的隨機數；S為螢火蟲當前更新代數。

3.6 最優模型確定

在滿足螢火蟲算法停止條件后，計算每一只螢火蟲自身的熒光亮度。設(Lz,mz,rz)滿足I(Lz,mz,rz)=max[I(L,m,r)]，此時預測模型LSTM(Lz,mz,rz)的平均絕對誤差取最小值，即為最優預測模型。

4 實例驗證

為驗證本文所提出方法的準確性和有效性，基于某鐵路局電務段2014年8月至 2019年5月約58個月的補償電容故障記錄，其中記錄了補償電容故障時間和數量等信息，按式(1)構建序列長度為112的故障數量時間序列，并用前100個故障數據訓練預測模型，再用后12個故障數據檢驗所構建模型的預測效果。

4.1 模型構建功能驗證

由式(1)構建補償電容故障數量時間序列X={x(i)|i=1，2，…,n}，見圖6。

圖6 補償電容故障數量時間序列

設LSTM循環次數L∈[2,12]，窗口長度m∈[5,30]，神經元個數r∈[5,60]。設尋優算法中螢火蟲數量M=20，步長因子α=0.2，光強吸收系數γ=1.0，最大吸引度β0=1.0，最大權重wmax=1.1,最小權重wmin=0.2，最大更新代數Smax=15。設測試集{Xte,Yte}樣本量為12，將除測試集外的剩余樣本按0.8和0.2的比例分為訓練集和驗證集，按第3節基于螢火蟲算法的預測模型超參數優化對超參數進行尋優，得到最優預測模型為LSTM(Lz,mz,rz)=LSTM(6,11,51)。

網絡訓練過程中，模型LSTM(6,11,51)在訓練集、驗證集和測試集的損失見圖7。

圖7 訓練過程中模型LSTM(6,11,51)在各數據集上的損失

由圖7可知，在AdaDelta算法迭代至110次時，預測模型在驗證集的損失達到最小，此時預測模型網絡參數相對最優。

4.2 模型預測性能驗證

為量化預測模型對故障數量序列的擬合效果，本文引入均方根誤差RMSE和平均絕對誤差MAE作為模型預測精度的評價指標，誤差越小擬合效果越好。

(16)

(17)

由式(16)和(17)求得預測模型的訓練集RMSE=0.825,MAE=0.625，測試集RMSE=1.224，MAE=0.833，說明預測模型較準確地挖掘了補償電容故障數量隨時間的變化規律，整體誤差相對較小。此外，訓練集與測試集的各評價指標之間相差不大，說明預測模型具有良好的泛化能力，并能夠達到較好的預測效果。

設訓練集均方誤差為RMSEtr，為更好地描述補償電容故障數量，假定模型預測誤差服從均值為0，方差為RMSEtr的正態分布，給出故障數量的取值范圍為

(18)

從而得到預測模型LSTM(6,11,51)在訓練集的擬合結果(見圖8)和在測試集的預測結果(見圖9)。

圖8 訓練集擬合結果

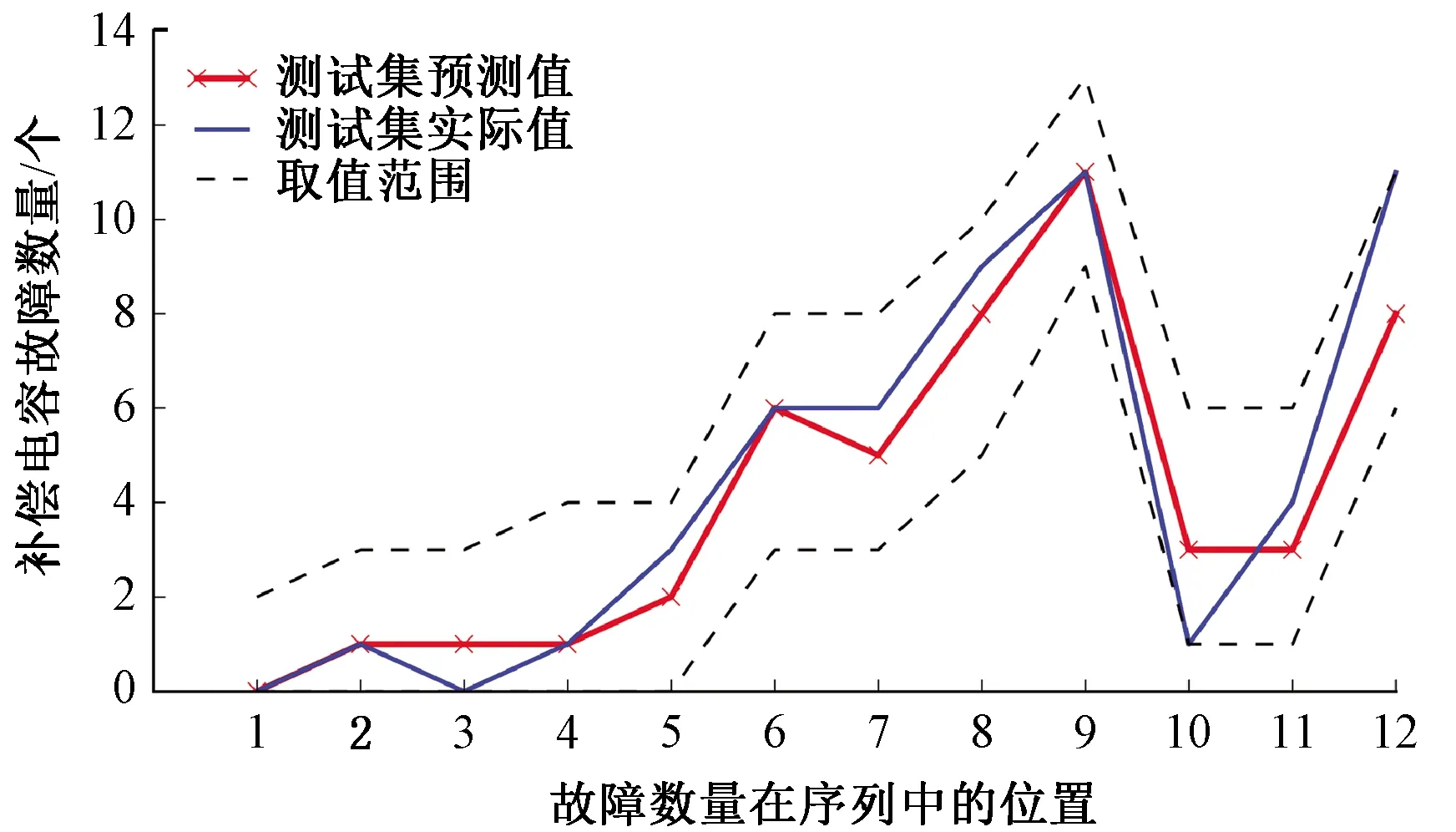
圖9 測試集預測結果

由圖8可知，預測模型擬合曲線與實際曲線大體吻合，且實際值基本處于取值范圍內，表明LSTM能較好地跟蹤補償電容故障數量隨時間的變化規律。由圖9可知，LSTM模型較好地預測了補償電容的故障數量，實際值均處于取值范圍內，預測值與實際值之間的最大絕對誤差為3，取得了良好的預測效果。

5 結束語

基于鐵路現場的補償電容故障記錄，本文提出了一種預測補償電容故障數量的方法。該方法首先根據補償電容故障記錄構建補償電容故障數量隨時間變化的序列；再基于LSTM構建了故障數量預測模型，針對LSTM初始化超參數對預測模型性能有較大影響的問題，利用螢火蟲算法對超參數進行優化，從而挖掘補償電容故障數量隨時間的變化規律，并實現對補償電容未來一段時間內故障數量的預測。實驗部分，某路局電務段的實際數據被用來檢驗本文方法各步驟的功能，實驗中對后12個數據點進行了預測，預測結果的均方根誤差和平均絕對誤差分別為1.224和0.833。可見，使用本文方法可以有效地預測補償電容故障數量，從而幫助鐵路部門提前協調設備、資金和維修人員等資源，為補償電容運維提供良好的指導，給補償電容故障預測的研究提供了新思路。