CRTSⅡ型板式軌道高溫穩定性的影響因素研究

劉笑凱，肖杰靈，趙春光，劉學毅

(1.中北大學 理學院，山西 太原 030051；2.中北大學 山西省地下空間工程研究生教育創新中心，山西 太原 030051； 3.西南交通大學 高速鐵路線路工程教育部重點實驗室，四川 成都 610031； 4. 西南交通大學 土木工程學院，四川 成都 610031)

CRTSⅡ型板式無砟軌道(以下簡稱Ⅱ型板)是一種典型的縱連式高速鐵路軌道結構(見圖 1)，主要包括軌道板、砂漿層和混凝土支承層等部分，軌道板上每650 mm布置一道假縫，相鄰板間設置寬窄接縫將縱向連結成一個整體。受列車荷載和溫度荷載的循環作用以及施工質量等因素的影響，Ⅱ型板可發生砂漿層離縫、軌道板裂紋、掉塊、上拱等病害，特別是局部地段會發生軌道板上拱現象，見圖 2，極端條件下甚至會發展成軌道結構的整體失穩，嚴重威脅行車安全及設備正常服役[1-2]。縱向連續結構垂向失穩很早就引起了專家的注意，Hobbs等[3]、Taylor等[4]研究得出剛性基礎上輸油管道的失穩模態和上拱位移與縱向力的關系，認為高溫下(升溫可達100 ℃)失穩主要是一種屈曲行為。國內學者對Ⅱ型板的各種病害進行了大量研究：高睿[5]、劉英等[6]研究了軌道板上拱后的整治問題，研究表明植筋是解決軌道板上拱病害的有效措施之一；Wang等[7]研究了砂漿層脫連后對軌道結構動力特性的影響，認為砂漿脫連寬度達到1.95 m就必須進行維修；劉亞男[8]研究了復雜溫度下寬窄接縫的病害問題，研究表明窄接縫缺損會造成鋼軌受力和變形增大、砂漿層脫粘以及軌道板的上拱；周敏[9]研究了簡支梁橋上的Ⅱ型板的穩定性，分析了砂漿層參數、簡支梁跨數及橋墩剛度對軌道結構穩定性的影響，并就如何防止軌道板上拱提出了幾點技術性措施。上述研究主要集中于Ⅱ型板結構發生失穩的風險、病害后的影響及整治措施等方面，為深入研究分析垂向穩定性的影響因素，確保結構的安全服役提供了重要參考。

圖1 Ⅱ型板結構簡圖

圖2 Ⅱ型板上拱

1 力學模型

參考壓桿失穩的基本理論，構件的初始缺陷是誘發失穩的關鍵因素，并可在一定程度上決定失穩的形狀和程度[10]。理想的平直軌道板在軸向力的作用下并不會發生垂向上拱。因此軌道板上拱的力學模型中應設置初始上拱。首先應研究軌道板上拱矢度與上拱波長的關系。

軌道板上拱后，板底與支承層完全脫連，根據失穩狀態和荷載作用條件，可簡化為剛性基礎上無限長的歐拉梁，見圖3。

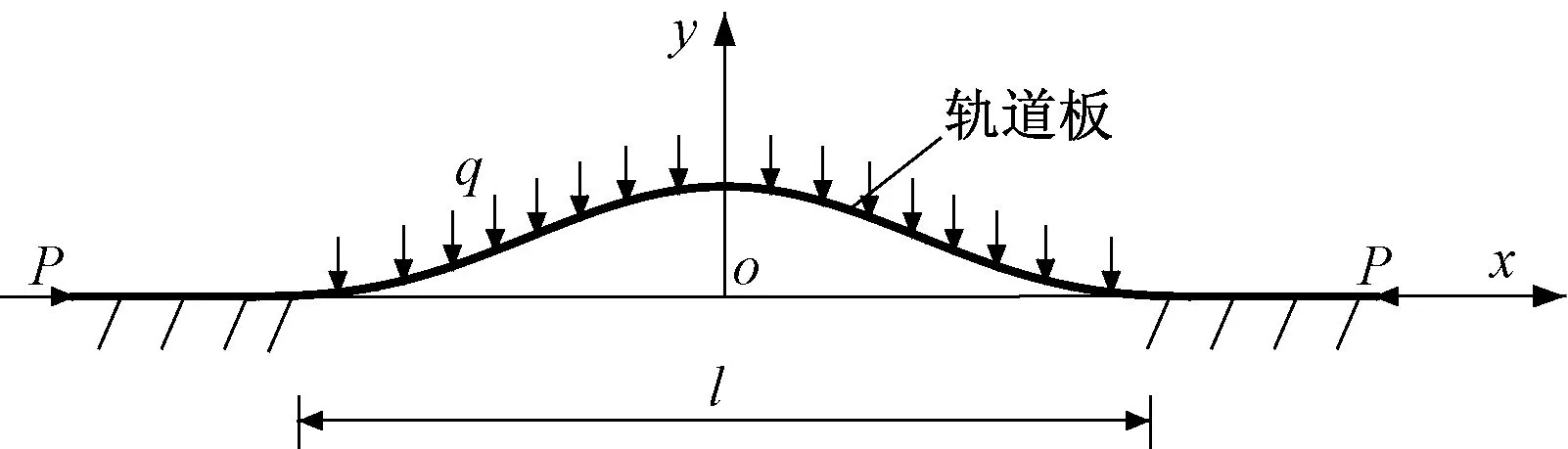
圖3 軌道板的垂向失穩變形曲線及受力圖

圖3中：l為軌道板上拱變形波長；q為軌道板重力荷載；P為軌道板內的縱向溫度力。

根據歐拉梁撓曲理論[3]，軌道板上拱部分(圖中標注長度為l)的控制方程為

(1)

式中：E為軌道板混凝土的彈性模量；I為軌道板的垂向慣性矩。

根據邊界條件：y(-l/2)=0，y(l/2)=0，y′(-l/2)=0，y′(l/2)=0，可以求得軌道板上拱部分的撓曲方程為

(2)

由軌道板上拱段端部的彎矩為零[11]，即y″(-l/2)=0可以得到軌道板上拱矢度與上拱波長的關系為

(3)

根據軌道板上拱線型建立其垂向高溫失穩的力學模型，見圖 4。模型考慮初始上拱，上拱段曲線滿足式(2)，上拱段長度即初始上拱波長為l0，初始上拱矢度為f0，上拱波長與上拱矢度滿足式(3)。

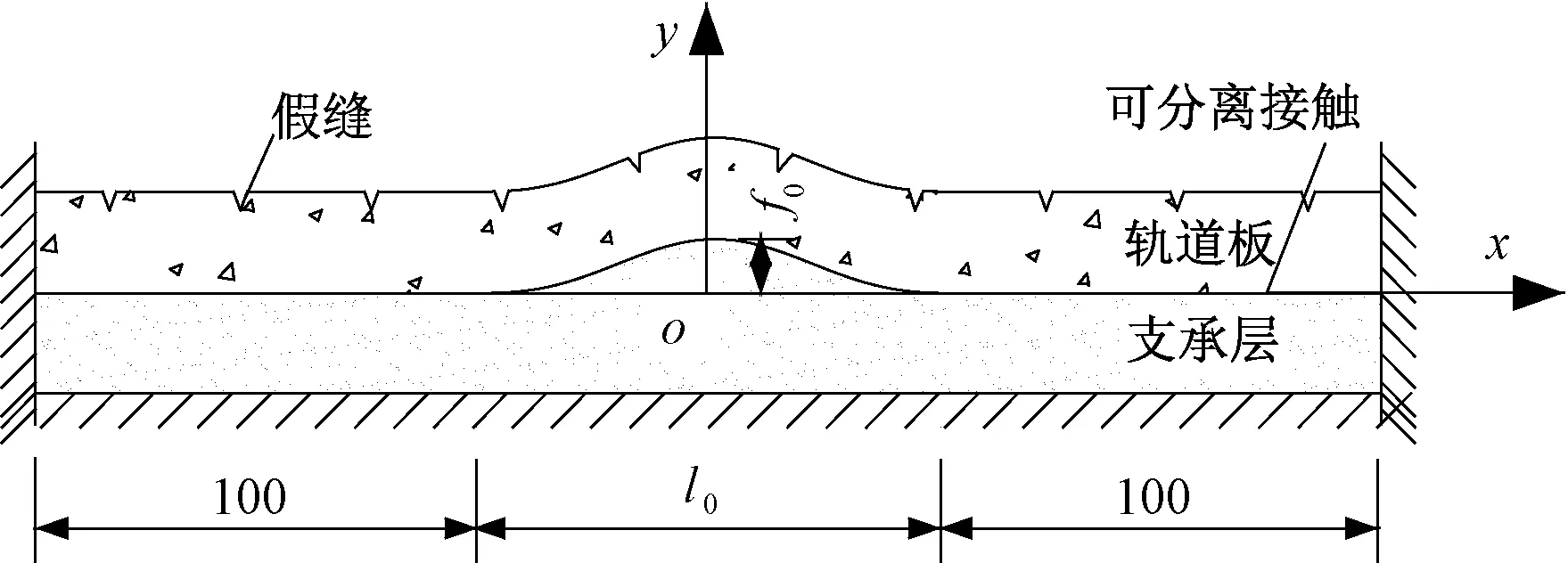
圖4 力學模型示意圖(單位：m)

在上拱段兩端各建長度不小于100 m的水平延伸段。軌道板與底座板之間為接觸關系，因軌道板的上拱伴隨著層間的脫連，故不考慮層間黏結。軌道板存在初始上拱時，底座板上表面線型與軌道板保持一致。軌道板兩端、底座板兩端和底面均處理為固定約束。不考慮軌道板的橫向影響，故模型可采用2D平面應力單元建模。考慮鋼軌時，鋼軌與軌道板通過扣件連接，鋼軌采用CHN60軌，并用歐拉梁單元模擬，扣件采用線性彈簧單元模擬。

主要參數見表1[1,8,12]。

表 1 主要計算參數

2 模型驗證

為驗證模型的正確性，運用解析法推導了理想板有初始上拱時，軌道板在溫度力作用下的上拱位移，并進行了模型試驗。

解析法在小變形的前提下假設軌道板上拱前后的線型均滿足其撓曲方程，即滿足式(2)。上拱前后矢度和波長滿足式(3)。如圖5所示，其中，實線為軌道板未上拱前的線型，虛線為軌道板上拱后的線型，上拱前軌道板的初始波長為l0，上拱后軌道板的波長為l，初始上拱矢度為f0，上拱后的上拱矢度為f[4]。

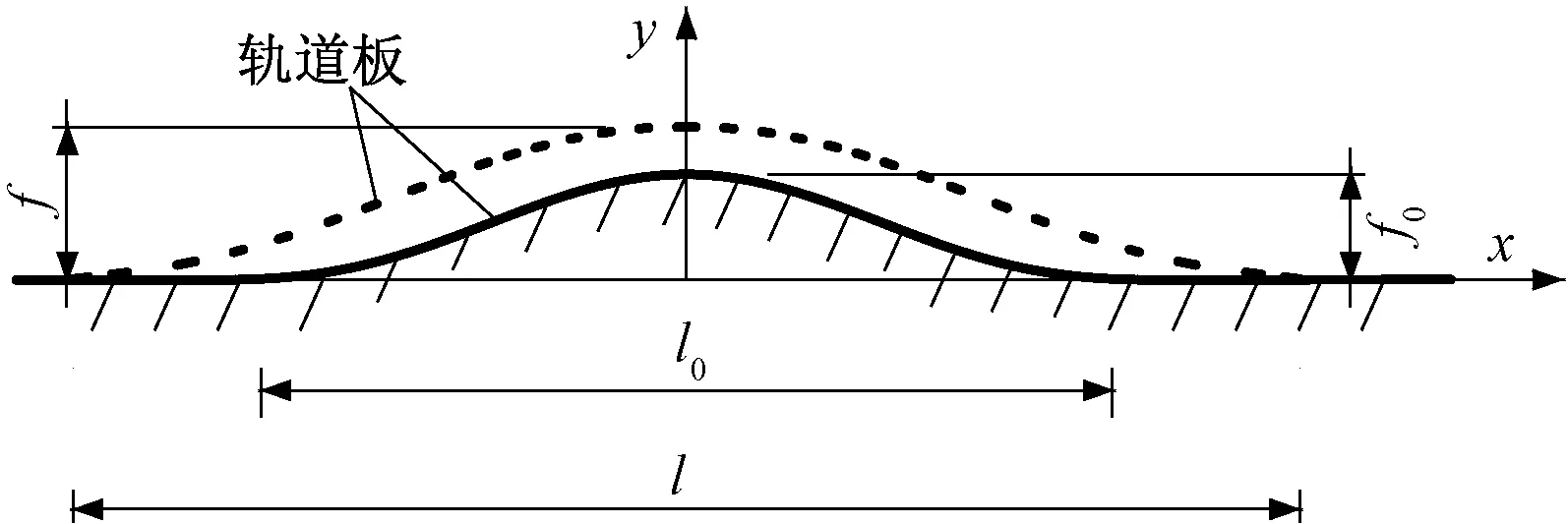
圖5 軌道板上拱前后的線型

根據勢能駐值原理[10]，可以得到在不同初始波長條件下，軌道板的縱向力隨波長的變化關系為

(4)

模型試驗按照1∶20的比例制作軌道板模型，板厚1 cm，板寬12.75 cm，模型有效長度為2.5 m，見圖 6。考慮到小尺寸條件下采用混凝土材料模擬道床存在加工精度低和材料均勻性不良等問題，軌道板采用鋁板進行模擬。兩端采用扣壓裝置實現垂向約束，右端為固定端，左端為加載端。加載端設置千斤頂，并通過滑軌實現縱向加載模擬軌道板的縱向溫度力作用。分別采用百分表、壓力傳感器采集模型的垂向位移和縱向壓力。軌道板上布置7個垂向位移測點，測點布置見圖7。

圖7 測點布置(單位：mm)

試驗結果與解析法和有限元法的計算結果見圖8。其中試驗最大上拱位移出現在中間測點處，解析法和有限元仿真所用f0均取1 mm(l0為1.73 m)，當上拱位移為0.5 mm時上拱波長為1.92 m，小于鋁板長度2.5 m。3種方法的結果較為接近，其中有限元法比試驗和解析法得到的縱向力稍小。這驗證了有限元法計算軌道板在溫度荷載作用下垂向穩定性的正確性。

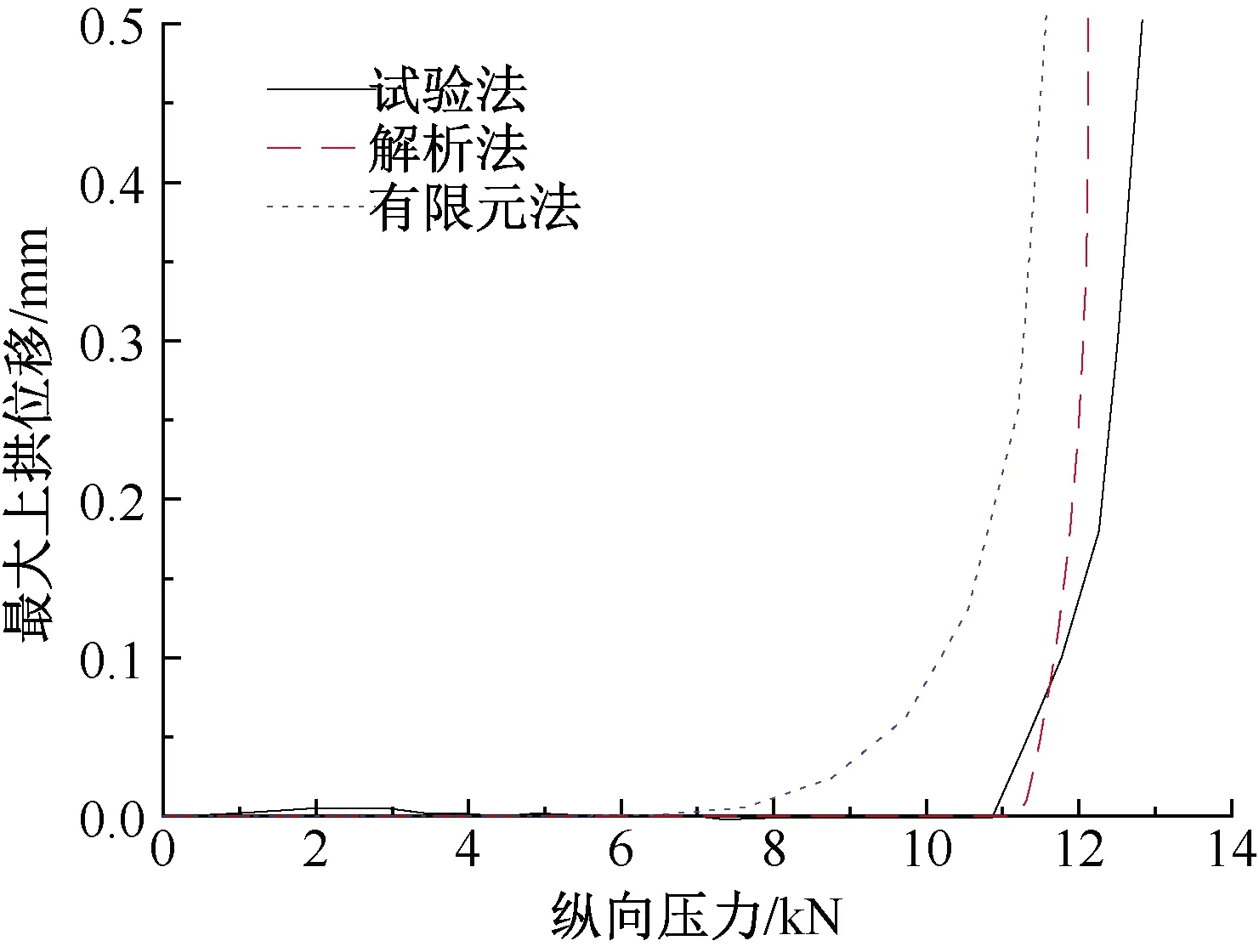
圖8 不同計算結果對比

3 影響因素分析

3.1 影響因素的分類

(1)初始上拱

根據鐵路無縫線路等穩定性研究成果[13]，初始變形是結構失穩的主要誘導因素，其存在有其客觀性。相對于CRTSⅡ型縱連板式軌道板而言，即為軌道板存在初始上拱變形，其成因有軌道板制作、施工或下部基礎變形等多種因素均可使軌道板產生初始上拱。

(2)溫度梯度

溫度梯度是無砟軌道結構的重要荷載形式之一，正溫度梯度會使軌道板產生向上的翹曲，負溫度梯度會使軌道板產生向下的翹曲，從而影響著軌道板的穩定。在初始上拱和溫度梯度共同作用下，可能會對軌道板的高溫穩定性產生不利影響。

(3)假縫

Ⅱ型板作為一種縱連式軌道結構，為了控制其裂縫的生成和發展，在相鄰的兩個承軌臺之間預設了寬38 mm、深28 mm的橫向假縫，假縫的存在降低了該處軌道板的垂向抗彎剛度，影響著軌道板的垂向穩定性。

(4)鋼軌

Ⅱ型板從上到下分別由鋼軌及扣件系統、軌道板、砂漿層和混凝土支承層組成。無縫化的鋼軌可視為一根細長的多點支承的受壓梁，其重力荷載直接通過扣件傳遞給軌道板，而其自身存在高溫垂向失穩的風險，這些必將影響或制約軌道板的垂向穩定性。

3.2 初始上拱的影響

對于受壓桿件而言，初始缺陷是誘發失穩的關鍵因素[10]，不同的初始缺陷，其失穩過程也不同，分別計算了f0=0、3、5、10、20 mm 5種工況，不考慮鋼軌和軌道板垂向溫度梯度，考慮假縫的影響。相關研究表明，無砟軌道在夏季內部的最高溫度在50 ℃左右[15]，計算中軌道板的最大整體升溫為50 ℃，計算結果見圖9。

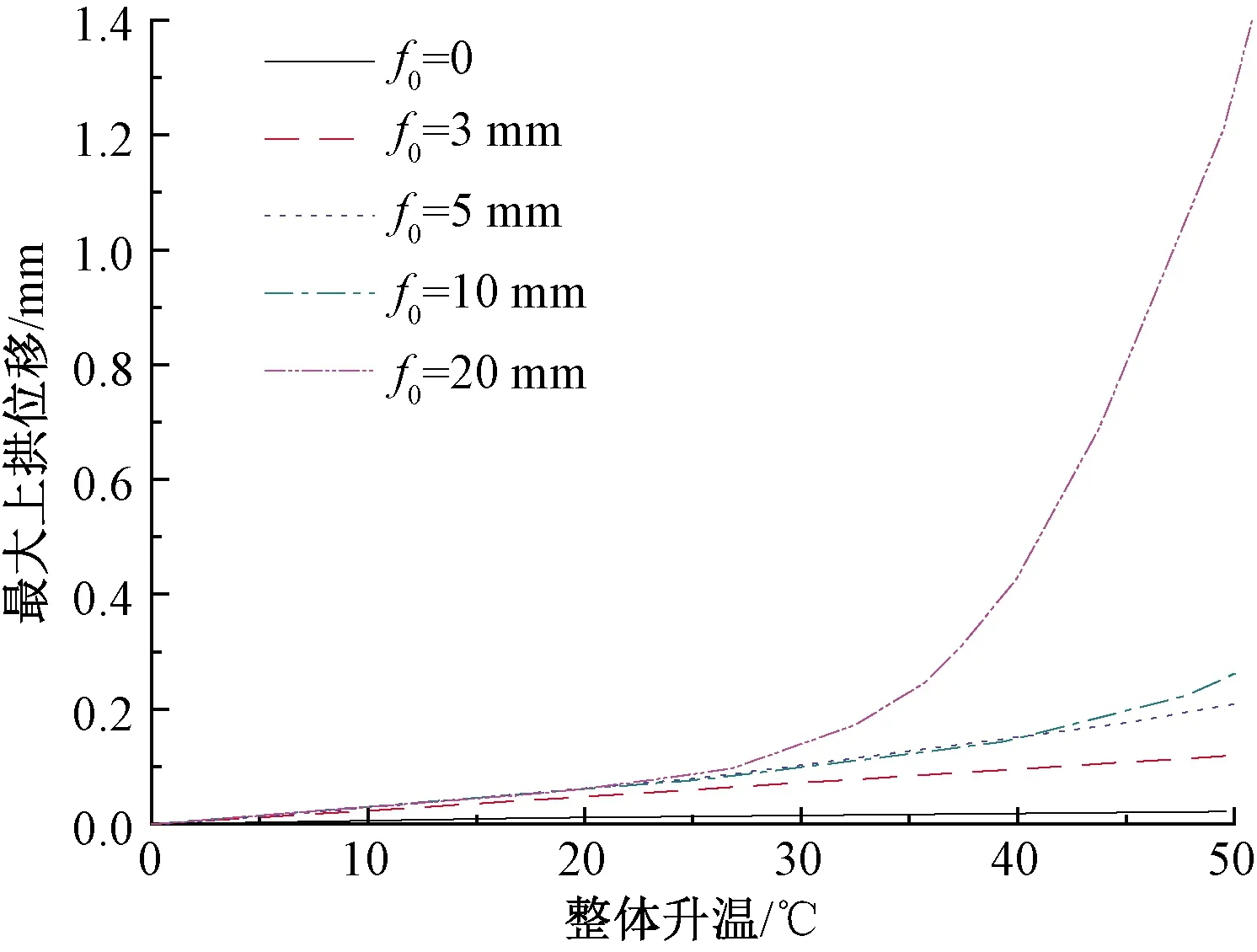
圖9 初始上拱的影響

由圖9可知，在初始上拱小于20 mm時，軌道板最大上拱位移隨整體升溫變化的曲線基本上為一條直線，在達到最大升溫時，軌道板的上拱位移分別為0.03、0.12、0.21、0.26 mm，當f0=20 mm時，當整體升溫大于35 ℃左右時，軌道板的最大垂向位移隨著溫度的升高迅速增大，進入脹板階段，當達到最大整體升溫50 ℃時，軌道板的最大上拱位移可達到1.26 mm。

3.3 溫度梯度的影響

在實際使用當中，軌道板上表面直接暴露于空氣當中，下表面與CA砂漿接觸，其吸熱量和散熱量不同，因此軌道板難以形成理想的整體升溫，在垂向必然有溫度梯度的存在，有溫度梯度作用時，軌道板在垂向的溫度應力分布不均，因而會產生翹曲變形[16-17]，這勢必會影響軌道板的穩定性。下面研究溫度梯度對軌道板穩定性的影響，其中f0為5 mm，溫度梯度為線性溫度梯度。現場實測資料表明，夏季軌道板最大正溫度梯度高達90 ℃/m 左右，最大負溫度梯度絕對值比最大正溫度梯度小[18]，計算中最大正負溫度梯度均取100 ℃/m，計算結果見圖10。

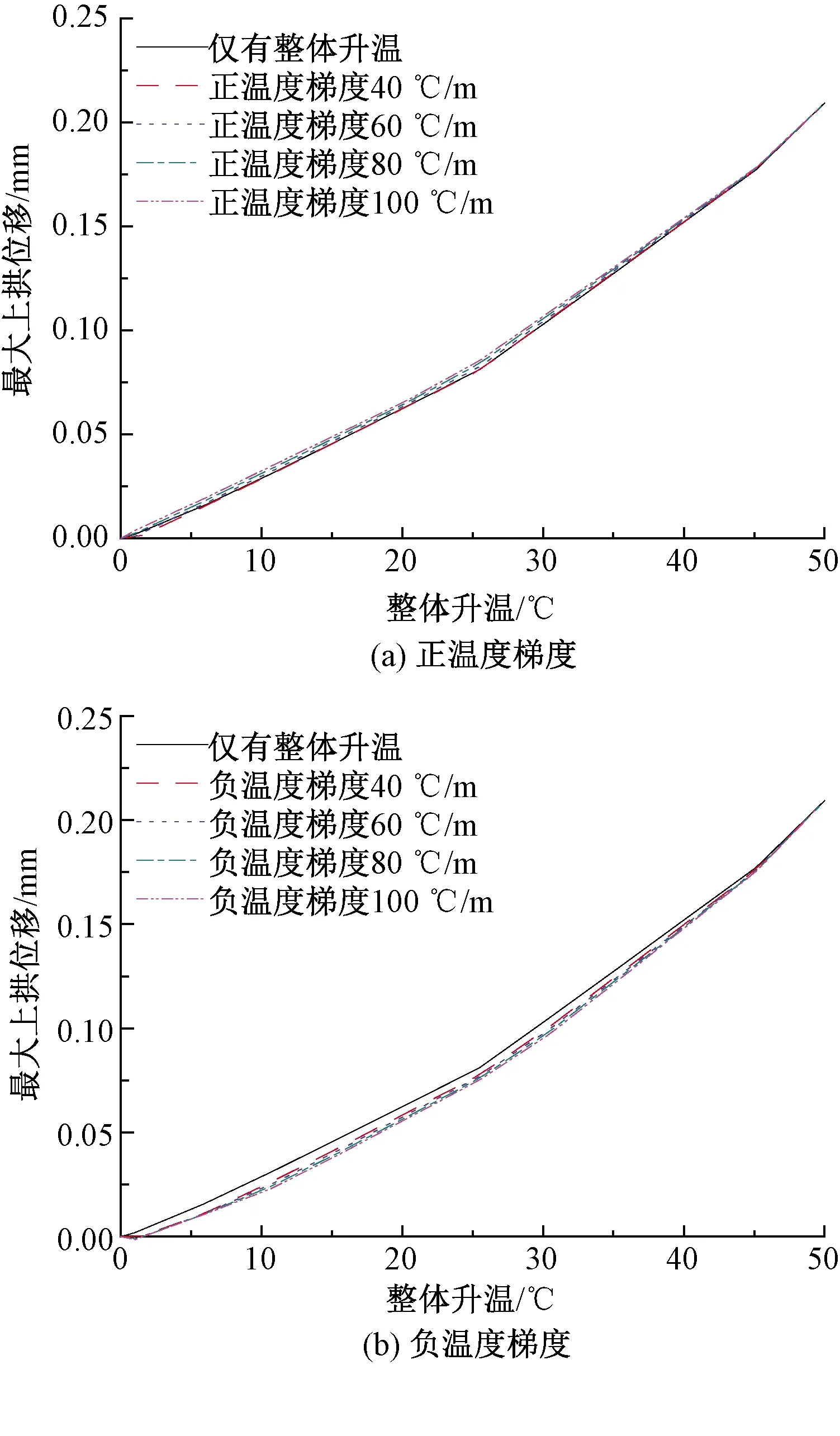
圖10 溫度梯度的影響

圖10表明，正負溫度梯度對軌道板穩定性影響均較小，必要時可以不加考慮。有正溫度梯度作用時，軌道板的最大上拱位移隨整體升溫的變化曲線處于僅考慮整體升溫時的上方，且溫度梯度越大，最大上拱位移越大，說明正溫度梯度會對軌道板的穩定性造成不利影響，正溫度梯度越大軌道板穩定性越低。在有負溫度梯度作用時，軌道板的最大上拱位移隨整體升溫的變化曲線處于僅有整體升溫時的下方，且負溫度梯度越大，最大上拱位移越小，說明負溫度梯度會增加軌道板的穩定性，且負溫度梯度越大軌道板穩定性越高。

3.4 假縫的影響

為了分析假縫對軌道板垂向穩定性的影響，分別對有、無假縫兩種工況進行了仿真比較，計算結果見圖11。

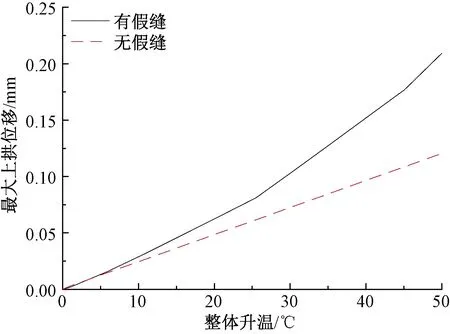
圖11 假縫計算結果

圖11表明，初始階段兩種工況下軌道板的最大上拱位移隨整體升溫增加而增加的趨勢基本一致；隨著整體升溫的增加到10 ℃以上時，有假縫時的最大上拱位移開始大于無假縫時，且兩者差值逐漸增大；在最大升溫50 ℃時，有、無假縫時的軌道板最大上拱位移分別為0.21、0.12 mm，兩者差達75%。上述仿真說明，假縫對軌道板初始階段的高溫脹板影響較小，隨著整體溫升的增加，有假縫時軌道板的剛度下降更快，將更容易導致軌道板高溫穩定性問題。

3.5 鋼軌的影響

參考相關文獻[15]，我國夏季鋼軌的軌溫最高約60 ℃，為安全計，計算中鋼軌的最大升溫取值為70 ℃。僅研究鋼軌升溫的影響，并不研究鋼軌的升溫過程，計算結果見圖12。

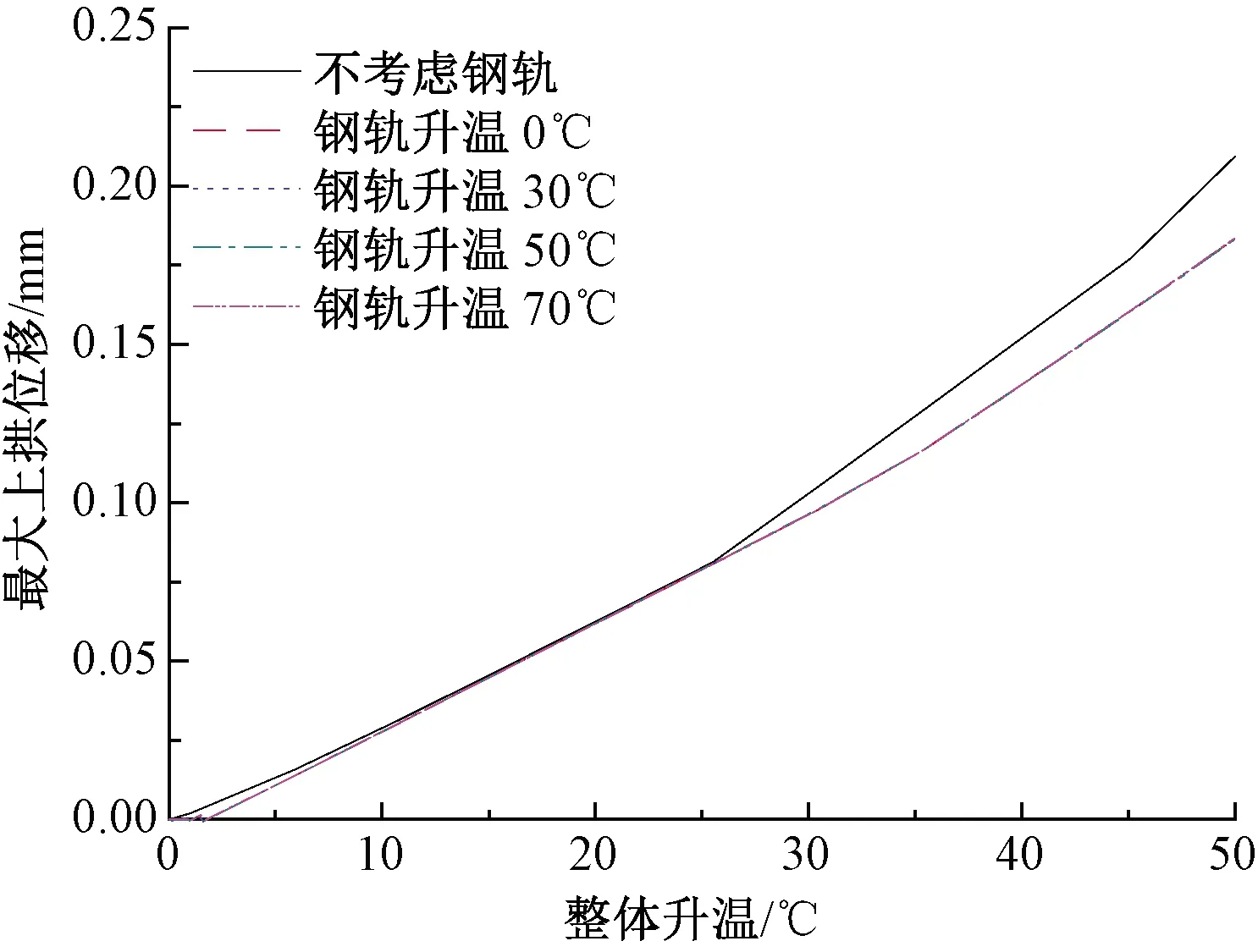
圖12 鋼軌升溫計算結果

從圖12可知，在整體溫升26 ℃以下時，鋼軌約束及其溫升均不會對軌道板的高溫穩定性產生影響；在整體溫升超過26 ℃時，考慮鋼軌時軌道板的最大上拱位移隨整體升溫的變化曲線處于不考慮鋼軌時的下方，這表明鋼軌的約束對增強軌道板的高溫穩定性是有利的；不同鋼軌溫升對軌道板高溫穩定性的影響基本一致。

由于鋼軌自身也會存在一定程度上的垂向初始不平順，在溫度力的作用下可能影響軌道板高溫穩定性。考慮鋼軌的初始不平順滿足式(2)，并參考相關研究[15]，鋼軌的最大初始上拱矢度取3 mm，不考慮鋼軌的初始彈性上拱，假設鋼軌升溫為70 ℃，鋼軌初始上拱對軌道板垂向穩定性的影響見圖13。計算表明，在軌道板整體溫升26 ℃以下時，鋼軌約束及其初始上拱均不會對軌道板的高溫穩定性產生明顯影響；在軌道板整體溫升大于26 ℃后，鋼軌存在初始上拱時，軌道板的最大上拱位移隨整體升溫的變化曲線與不考慮鋼軌初始上拱時接近，當鋼軌初始上拱3 mm且升溫70 ℃時，軌道板的穩定性與不考慮鋼軌時基本相當，表明鋼軌的初始上拱可降低軌道板的穩定性，并抵消其重力對軌道板垂向穩定性的制約。

圖13 鋼軌初始上拱對軌道板垂向穩定性的影響

4 結論

經有限元法模型仿真，研究了Ⅱ型板垂向穩定性的相關因素，重點分析了初始上拱、溫度梯度、假縫和鋼軌對軌道板穩定性的影響，主要結論如下：

(1)軌道板初始上拱是其高溫穩定性的主要影響因素，初始上拱矢度越大，軌道板的穩定性越差，當f0≥20 mm(l0≤22.1 m)時，軌道板在35 ℃左右時進入脹板階段，有整體失穩的危險，應當控制施工質量使f0<20 mm。

(2)溫度梯度對軌道板穩定性的影響較小，正溫度梯度會降低軌道板的穩定性，負溫度梯度對軌道板的穩定性有利，這表明整體升溫是影響軌道板穩定性的主要荷載形式。

(3)當軌道板溫升10 ℃以上時，假縫將降低軌道板的穩定性，且軌道板整體溫升越大，假縫影響越明顯。

(4)鋼軌約束對軌道板的穩定性是有利的，但鋼軌升溫后有利程度降低；鋼軌有初始上拱與和不考慮鋼軌時軌道板的穩定性基本相當，此時鋼軌對軌道板的穩定性影響很小。