基于Modelica語言的ROV力學系統建模與仿真

韓 楓，謝基榕

（中國船舶科學研究中心深海空間站研究設計部，江蘇無錫214082）

0 引 言

在ROV 的運動建模過程中，存在較強的非線性特性，且不同自由度間的耦合作用十分明顯，尤其是水動力學部分。傳統Simulink 建模方式本質上仍是確立系統的輸入輸出量后，將系統的微分代數方程推導為狀態空間表達式，以確定的因果運算機制建立并求解仿真模型。當涉及此類多變量、非線性與多耦合的復雜系統建模時，采用此方式需花費大量時間進行因果賦值運算。與之相比，Modelica語言具有非因果建模特性，即聲明方程時不限定方程求解方向，可極大簡化建模工作量。

本文依據Fossen提出的針對一般水下航行器的運動建模理論[1]并應用Modelica建模語言，以ROV力學系統為例，提出一種通用的、面向對象的水下航行器運動建模方法；對ROV 進行動力學、運動學分析，對于流體動力部分針對其運動特性單獨闡述、簡化；應用Modelica 語言面向對象特性，劃分系統仿真框架如圖1所示，在基于該語言的MWorks平臺內，形成ROV動力學、運動學子系統下各模塊由受力模型到仿真模型轉化，通過組件實例化與基類繼承的方式實現模型重用，創建ROV 力學系統。最后，將推進器動態性能仿真應用至ROV 斜航與下潛仿真工況中，對仿真結果進行分析，以展示建模方法的合理性、快捷性。

圖1 仿真框架與系統層級劃分Fig.1 Simulation framework and system hierarchy division

1 Modelica語言特性

Modelica 是一種面向對象、采用非因果建模與陳述式建模的多領域物理系統建模語言，可應用于幾乎所有工程領域[2]。該語言采用基于方程的方法描述真實物理系統，其內置的Modelica標準庫包含了機、電、液、熱、控等多領域的基礎組件模型，可實現對現代復雜工程系統進行整體性能分析與評估的任務。

Modelica 語言應用面向對象的思想[3]，支持采用分層機制、組件連接機制和繼承機制構建模型[4]，可簡化模型結構的復雜程度。不同于Simulink 建模需要將數學模型推導為因果關系明確、數據流向恒定的狀態方程，該語言采用方程定義變量的行為，無需人為劃分方程求解方向，求解器根據給定條件自行求解未知量。該語言可根據系統的真實物理拓撲結構進行建模，其組件視圖具有與真實系統相似的結構層次與布局。

2 水下航行器運動學建模

采用ITTC 推薦坐標體系描述水下航行器六自由度運動，如圖2 所示。使用歐拉角法描述航行器姿態角[5]，航行器位置和姿態矢量表述為

航行器速度與角速度矢量在動系中投影為

利用剛體有限轉動理論和歐拉旋轉定理[5]，可推導速度、角速度從其在動系中投影v到其在定系中投影η˙的轉換矩陣J1(η2)、J2(η2)，兩者共同構成水下航行器運動學轉換矩陣J(η2)：

圖2 水下航行器定系與動系定義Fig.2 Definition of fixed and moving coordinate system of underwater vehicle

3 水下航行器動力學建模

將航行器所受外力（矩）劃分為慣性力-τ、流體動力τH、靜力τR、推力τP、外界干擾f 等部分，建立動系內動力學平衡方程：

式中各項皆為六行列矢量，列矢量的前三行、后三行元素分別表示該力、該力矩在動系中的投影。

3.1 剛體動力學建模

將航行器視為剛體，對動系原點應用動量定理與動量矩定理，可得到剛體動力τ矢量形式：

式中，MRB是航行器對動系原點的剛體質量與慣性張量矩陣；CRB是由航行器繞動系旋轉引起的科里奧利力與向心力矩陣。根據達朗貝爾原理，動系作為非慣性系，在其中進行受力分析時，需將剛體動力取負值-τ，作為慣性力參與到平衡方程的求解中。

3.2 流體動力學建模

將航行器所受流體動力τH劃分為與加速度v˙相關的慣性力τA和與速度v相關的粘性力τD。將慣性類流體力τA按附加慣量矩陣MA和由MA引起的科氏力和向心力矩陣CA的形式分離為

由ROV的對稱性假設，可將其附加慣量矩陣MA中非對角線元素消去，矩陣CA亦受到簡化。

將航行器所受粘性類流體力τD分離為

式中，D為水動力阻尼矩陣，可將其分解為線性、非線性水動力阻尼矩陣DL、DNL兩項：

由ROV 對稱性假設，且其大部分運動皆在水平面與垂直面內進行，運動速度一般為低速，可忽略其水動力阻尼的耦合效應，視粘性水動力系數為相互獨立，并忽略二階以上水動力系數的影響。

航行器受洋流U 作用時，先于定系中描述洋流速度與角速度投影vU，再于動系中利用轉換矩陣J(η2)-1求其投影vtransU并計算航行器相對洋流的速度與角速度投影vr，其結果用于計算流體動力τH。

3.3 靜力學建模

航行器受靜力τR作用，包括重力G、浮力B 和浮心位置rB的影響，需先計算靜力于定系中垂向投影，再利用速度投影轉換矩陣的逆陣J1(η2)-1求取其于動系中投影，由浮心位置rB計算恢復力矩。

3.4 推進系統建模

推進系統模型可劃分為電樞模型與推力模型，前者用于計算外部電壓作用下電機輸出轉速，經推力系數、轉矩系數擬合后，可求得標量形式表述的螺旋槳軸向推力與軸向轉矩；后者則定義螺旋槳位置和角度，從而獲知軸向推力及轉矩、推力在質心處轉矩的矢量形式，并求其在動系內投影。

對推進系統中直流電機的電樞部分進行建模，其簡化模型組件視圖如圖3所示。列寫其回路電壓平衡方程與轉軸轉矩平衡方程：

圖3 電樞模塊組件視圖Fig.3 Components of armature module

式中，R、L、i 分別是電樞電路中電阻、電感與電流，Vs為輸入電壓，E 為反電動勢E = Ceω，Ce為反電動勢系數，ω 為電機轉動角速度；fm為電機轉軸粘性摩擦系數，Mm為電磁轉矩，Mm= Cmi，Cm為轉矩系數，Q為螺旋槳切割水流引起負載轉矩，Jm為電機與負載折合至轉軸的總轉動慣量。工程應用中因摩擦系數fm較小可將其忽略，消去中間變量i、E、Mm后，得到以角速度ω 為輸出，以電壓Vs和負載轉矩Q 為輸入的直流電機微分方程；在零初始條件下對其進行拉氏變換，根據線性疊加原理，可分別求得Vs與Q到ω的傳遞函數：

式中，Ki（i=1,2）為增益常數，Ti（i=1,2,3）為時間常數，均為電機固有參數。可聯立以推力系數KT、轉矩系數KQ表述的推力T 及負載轉矩Q方程：

式中，n、D分別為螺旋槳轉速、直徑。

已知第i 個推進器相對動系的位置矢量riP與角度θi和Ψi，如圖4 所示。獲知其軸向推力標量Pi、扭矩標量Qi后，可求取該推進器推力、扭矩、推力矩矢量在動系內投影，對各推進器上述矢量投影求和即得總推力（矩）矢量τP。

圖4 單個推進器安裝位置與角度Fig.4 Installation position and angle of a single propeller

4 水下航行器通用仿真模型建立

根據已分析的水下航行器運動模型與Modelica 語言面向對象的特征，提出一種通用的水下航行器運動建模方法，以ROV 力學系統為例，將其劃分為動力學與運動學兩個子系統，共下設五個模塊：慣性力模塊、流體動力模塊、靜力模塊、推進模塊（可進一步劃分為電樞模塊與推力模塊）和運動學模塊，各模塊關系與功能如圖5所示。

應用基于組件的建模方法，定義可重用、包含不同變量類型的多個連接器類，在本文中應用如表1所示。模塊內通過連接器實例化方式獲取所需變量，模塊間則通過連接器互聯完成信息傳輸。

欲創建各力學模塊，除定義和獲取所需變量外，還需在參數區定義相關的模型參數。由于同一參數可能在不同模塊內多次出現，為避免冗余，本文將ROV 物理參數與水動力系數集成后單獨創建模塊，并通過繼承方式將參數傳遞至各力學模塊。

圖5 ROV力學系統各模塊功能Fig.5 Function of each module of ROV mechanical system

表1 連接器內定義變量類型Tab.1 Variable types defined within the connector

以創建流體動力模塊為例，首先在MWorks 平臺內定義運動學連接器ROV_ve?locity，其中聲明速度變量u、v、w 與角速度變量p、q、r，如圖6（a）所示；隨后建立流體動力模塊并繼承物理參數模塊ROV6dof_parame?ters以獲取水動力系數，將連接器ROV_veloc?ity 實例化為對象p，并創建式（8）中非線性水動力阻尼矩陣DNL，如圖6（b）所示。

運用類似方式定義力與力矩連接器實例p1、附加質量矩陣MA、科氏力與向心力矩陣CA、線性水動力阻尼矩陣DL。如圖6（c）所示，在equation 塊內建立守恒方程，為避免繁瑣，用多維數組V 指代速度與角速度變量，利用微分算子der()對時間求導功能計算（角）加速度，由流體動力式（6）～（8）所示，等式左側取各矩陣變量與（加）速度、角（加）速度變量進行符號運算，等式右側連接器實例p1內嵌套的力與力矩變量F即為流體動力tau_H。在此模塊的圖標視圖內繪制圖像，則流體動力模塊封裝完畢，可通過內置的運動學與動力學連接器進行模塊間信息交互。

運用上述建模方法建立并封裝各力學模塊，在頂層模型中完成模塊實例化，其圖標視圖如圖7所示。對各模塊實例的連接器進行匹配，連接器內勢變量生成等值的運動學兼容方程，保證了各模塊中速度、角速度、姿態角的一致性；連接器內流變量則統一各動力學模塊，自動生成如式（4）所示的各受力項之和為零的動力學平衡方程，從而建立起完備的ROV 運動微分方程組。至此完整的ROV 力學系統建立完畢，設定作業工況即可進行仿真。

圖6 流體動力模塊建立過程Fig.6 Establishment process of hydrodynamic module

圖7 MWorks中ROV力學系統頂層模型視圖Fig.7 Top-level model view of ROV mechanical system in Mworks

5 仿真實例

選取文獻[6]中ROV 為本文仿真對象，其主體及水動力系數如表2～3 所示，其推進器鏡像布置情況如圖8 和圖9 所示。水平推力T1～T4、垂向推力T9由1002 型推進器產生，垂向推力T5～T8則由1004型推進器產生，前者推力約為后者四倍。

表2 ROV主體物理參數Tab.2 ROV main physical parameters

表3 ROV水動力系數(有量綱)Tab.3 ROV hydrodynamic coefficients(with dimension)

圖8 水平方向推進器布置Fig.8 Horizontal thrusters configuration

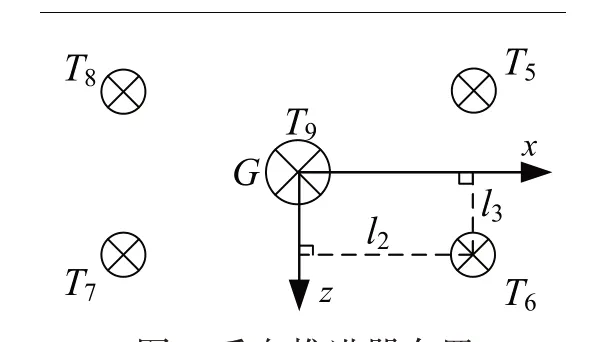
圖9 垂向推進器布置Fig.9 Vertical thruster configuration

將推進器輸入電壓與輸出推力進行歸一化處理，略去轉速生成過程并整合軸向負載轉矩影響，使用一階傳遞函數擬合推進器正轉與反轉過程中推力零初始條件下的動態性能，以采用的1002 型推進器[6]動態響應仿真曲線為例，如圖10 所示。

設置仿真工況為ROV 在垂直面內做斜航下潛運動，仿真持續時間20 s，應用推進器動態響應仿真結果。垂推始終產生沿垂軸正向的較小合推力，前10 s 內水平推進器滿載工作，合推力沿縱軸正向，10 s 后水平推進器斷電。ROV 初始速度、姿態角與各推進器推力均為零，全程采用默認Dassl 求解器運算，解出其運動軌跡如圖11 所示，其速度、姿態角及所受流體阻力變化過程如圖12所示。

由圖12（a）可知，仿真前10 s 內ROV 由靜止開始逐漸加速，直至推力τP、靜力τR與流體動力τH相平衡時保持勻速斜航；圖12（b）顯示，此過程中縱傾角θ 亦稍增長后保持穩定，這是小攻角來流條件引起的孟克力矩[7]M =( )Xu˙- Zw˙uw 所造成的，體現出ROV 航行過程中縱向速度u 和垂向速度w 的耦合由于流體粘性力τD的大小與速度及速度二次項均相關，ROV加速過程中初始流體阻力τH遠低于推力τP，經過一段時間加速后，流體阻力τH快速增長，ROV 接近受力平衡狀態，速度u及縱傾角θ的變化速率趨緩，其非線性運動特性得以展現。

圖10 推進器正、反轉動態性能Fig.10 Dynamic performance of thruster in forward and reverse directions

圖11 ROV運動軌跡Fig.11 ROV trajectory

圖12 ROV運動仿真結果Fig.12 ROV motion simulation results

仿真10 s后縱向推力τP逐漸歸零，在剛體慣性與流體粘性力τD的作用下，ROV 縱向速度u不斷減小至零，由于恢復力矩作用，縱傾角θ歸零，ROV回歸正浮、勻速下潛狀態。

由圖12（c）可知，流體慣性力τA對姿態角的影響更為顯著，這是由于其科氏力矩陣CA中包含了不同自由度間慣性水動力系數與速度的耦合項；由圖12（d）可知，粘性力τD縱向分量的數值較大，為影響ROV速度的主要因素，慣性力τA縱向分量僅在加速、減速初期產生較明顯的非線性變化效應。

6 結 語

本文將Modelica語言應用到ROV力學系統的建模過程中，提出了一種通用的、面向對象的水下航行器建模方法，該語言如下特性與優勢得以展現：

（1）陳述式特性更大限度地保留了力學系統理論拓撲結構，便于實現受力分析到仿真模型轉化；

（2）層級劃分機制使得圖標視圖與組件視圖中的各級組件更為清晰，有利于模型的修改與測試；

（3）非因果特性在進行此類非線性、多耦合的復雜系統建模時優勢明顯，無需人工劃分方程組數據流向，大大減少了建模工作量；

（4）繼承與組件實例化機制提升模型重用性，通過定義可重用的動力學與運動學連接器并應用組件連接機制，模塊間的互聯得到保證。

將推進器動態性能仿真應用至ROV斜航下潛仿真工況內，仿真結果體現出ROV在實航過程中非線性及不同自由度間運動耦合的力學特性，該建模方法的合理性、便捷性得以展示。同時，該語言多領域建模特性保留了對ROV 真實物理系統實施進一步探究的可行性，為后續機、電、液、熱、流等不同學科領域子系統接入提供了可能。