旋轉翼對海洋立管渦激振動抑振的數值研究

王 偉，宋保維，毛昭勇，田文龍，張婷穎

（1.西北工業大學航海學院,西安710072；2.無人水下運載技術工業和信息化部重點實驗室,西安710072）

0 引 言

渦激振動是一種在海洋工程領域較為常見的流固耦合現象。當海洋立管受到海流作用時，在立管結構后方會產生脫落的漩渦，周期性脫落的旋渦使結構產生橫向的脈動力，從而使結構發生周期性振動。尤其當渦脫落的頻率處于結構振動的固有頻率附近時，會發生頻率鎖定的現象，此時結構處于高振幅運動狀態，易造成結構的疲勞損傷或直接破壞[1-2]。海洋立管結構易發生渦激振動，如何減小立管結構因渦激振動產生的疲勞損傷或破壞具有重要的工程意義[3]。

目前，常見的渦激振動控制方法分為主動控制和被動控制兩大類[4]。文獻[5]通過實驗研究了粗糙帶對結構渦激振動的抑制作用，振幅最優可以降低30%左右；文獻[6]通過數值模擬研究了不同形狀的整流罩對立管結構渦激振動的控制作用；文獻[7]通過數值模擬研究了控制桿對立管渦激振動的抑振效果；文獻[8]通過數值模擬研究了尾流分隔板對立管結構渦激振動的抑振作用，發現C型尾流板可以有效抑振。上述方式均為常見的被動控制方法，此類方法較為簡單，但控制效果有限。不同于被動控制方法，主動控制方法需要額外的能量輸入，但主動控制方法更為有效，且受外界因素的影響小。文獻[9]通過實驗研究了一種電制動器對立管結構渦激振動的控制作用；文獻[10]通過實驗研究了一種主動反饋控制方法對立管結構渦激振動的控制作用；文獻[11]通過實驗研究了表面吹吸對立管結構渦激振動的控制作用；文獻[12]通過實驗研究了壁面加熱的方法。

旋轉翼屬于主動控制方法的一種，通過在立管結構上安裝旋轉的NASA 翼來達到抑振的目的。文獻[13]和文獻[14]分別通過數值模擬和實驗方法研究了立管自身旋轉的抑振效果，發現抑振效果較好。立管自身旋轉在工程應用中存在較多的困難，而通過安裝旋轉翼來控制海洋立管的渦激振動存在很多優勢：（1）NASA 翼是一種在航空領域應用廣泛的低阻外形結構，旋轉時阻力小，輸入的能量也相對較小；（2）相較于其它主動控制方法，裝置安裝較為簡單；（3）相較于被動控制方法，控制效果不受外界環境的影響，控制具有全向性。

本文提出了一種安裝旋轉翼來達到控制海洋立管渦激振動的方案，采用非定常數值計算方法對二維海洋立管渦激振動特性進行數值模擬。數值模型采用k-ω/SST 湍流模型，建立單自由度渦激振動模型，并采用Newmark-β法求解單自由度渦激振動方程。最后，詳細討論了旋轉翼對海洋立管渦激振動的控制影響。

1 物理模型

1.1 旋轉翼設計

旋轉翼的翼型采用NASA0015 翼型，翼型的特征長度（h）為50 mm，NASA 翼具有低阻特性。立管的直徑（D）為250 mm，旋轉翼質心距離圓柱表面距離（G）為125 mm，旋轉翼的數量為4，圖1所示為模型示意圖[15]。旋轉角速度的計算參數設置如表1所示。

圖1 安裝旋轉翼圓柱的示意圖Fig.1 Diagram of marine riser with rotating wings

表1 計算參數的設置Tab.1 The setup of calculating parameters

1.2 渦激振動的表征參數

為便于分析和描述，定義與渦激振動相關的無量綱化表征參數如下：

雷諾數Re

阻力系數Cd

升力系數Cl

振幅比A*

頻率比f*

約化速度Ur

式中：ρ為海水密度；U 為來流速度；μ 為動力粘性系數；Fx為立管所受阻力；Fy為立管所受升力；D 為立管的直徑；S為立管迎來流方向的特征表面積，對于二維數值計算來說，S=D；A為立管的振幅；fs為立管渦脫落的頻率；fn為立管的固有頻率；ω為旋轉翼旋轉的角速度。

2 數值模型

2.1 單自由度渦激振動方程

立管結構單自由度渦激振動的物理模型可以簡化為質量-彈簧-阻尼振動系統（如圖2所示）。考慮豎向振動方程：

圖2 渦激振動系統簡化示意圖Fig.2 Diagram of a simple VIV system

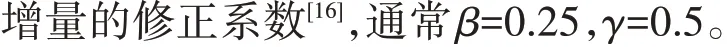
2.2 控制方程和湍流模型

不可壓縮流動問題的求解控制方程主要為連續方程和Navier-Stokes方程，即

求解選用的湍流模型為k-ω SST 模型，該模型能夠很好地處理近壁處低雷諾數的數值計算。該模型假設湍流黏度與湍流頻率的關系為

湍流強度k滿足

湍流頻率ω滿足

式中，a=5/9，b=0.09，c=0.075，σk=σω=2。

2.3 計算域和邊界條件

在實際流體數值計算過程中，為了避免計算域過小或過窄導致的計算誤差，將計算域設為40D×60D 的矩形區域，立管對計算域的阻塞度等于2.5%。海洋立管位于水平對稱軸上，且距離入口邊界為20D。計算域分為隨體域、旋轉域、振動域和外流場域。隨體域為6D×6D 的正方形區域，其用于包裹立管和旋轉域；旋轉域用于包裹旋轉翼；隨體域和振動域之外的計算域均為外流場域（計算域示意圖如圖3所示）。

邊界條件設置如下：（1）入口邊界（inlet）為速度入口；（2）出口邊界（outlet）為壓力出口；（3）上下遠場為對稱邊界（symmetry）；（4）海洋立管壁面（wall）為普通壁面；（5）隨體域、旋轉域、振動域和外流場域之間的交界邊均設為interface。隨體域、旋轉域與立管壁面具有相同的振動運動規律；振動域為網格變形區域，網格變形采用鋪層方法。

圖3 計算域示意圖Fig.3 Diagram of computational domain

2.4 網格劃分

利用ANSYS ICEM CFD15.0對模型進行網格劃分，為提高計算的精度，隨體域和旋轉域網格加密，且采用適應性較好的非結構化網格；振動域和外流場域采用結構化網格，網格較為稀疏，網格劃分如圖4所示。

圖4 網格處理Fig.4 Mesh generation

數值計算的壓力-速度耦合采用Couple 算法；模擬求解的格式均為精度較高的二階迎風格式；控制方程的離散格式為Standard方法。殘差收斂標準均設為1×10-5；計算步數為15 000步。立管結構和流場的耦合作用通過Fluent中的動網格技術來實現，立管結構所受流體力由Fluent中的流體數值算法求解；振動微分方程采用Newmark-β法求解；網格運動的速度和位移由Fluent 提供的宏訪問更新。

3 數值模型驗證

圖5 網格無關性驗證Fig.5 Results of the grid verification

網格會影響數值計算結果，因此有必要進行網格無關性驗證。改變圓柱體結構表面的網格節點數和第一層網格的高度使得網格數分別為110 000、150 000、165 000 和175 000。圖5 所示為不同網格數量下立管結構渦激振動的振幅比曲線，計算條件為Re=100 000（Ur=4.0）。由圖可知：網格數為165 000 和175 000 的圓柱體在振幅穩定后，結果相差不大。因此可以認為當網格數大于175 000 時，網格尺寸基本不會對計算結果產生影響。

為確保數值模型的精確性，有必要進行實驗驗證。計算條件與文獻[17]中的實驗條件相同，計算的約化速度范圍為2～14。計算結果同文獻[17]中的實驗結果以及文獻[18]中的數值結果進行比對，對比結果如圖6 所示。由圖可知，本文數值模型計算結果的變化趨勢與實驗結果的變化趨勢基本相同，建立的數值模型可以較準確地預測立管結構渦激振動的振幅特性和頻率特性。

圖6 數據對比Fig.6 Comparison of the characteristic results

4 計算結果與分析

4.1 旋轉角速度對立管結構渦激振動抑振的影響

由圖6 可知，當約化速度Ur=4.5 左右時，立管結構處于高振幅響應狀態，以該約化速度為計算條件，對比分析T1～T9 立管的渦激振動響應。圖7 所示為海洋立管渦激振動響應與旋轉翼旋轉角速度的關系（Ur=4.5），由圖可知：（1）隨著旋轉翼旋轉角速度的增加，立管的振幅比逐漸減小，最后基本不變；當ω=3.0 rad/s 時，振幅比接近于0，抑制振動效果十分明顯；（2）隨著旋轉翼旋轉角速度的增加，立管渦脫落的頻率比先減小，后趨于不變；當旋轉角速度大于2.0 rad/s 時，頻率比開始迅速下降；當ω=3.0 rad/s時，頻率比接近于0，抑制渦脫落的效果十分顯著；（3）當ω=3.0 rad/s時，海洋立管渦激振動的抑振效果已經十分明顯，振幅比從0.98 下降到0.008，振幅比降低99.2%；當旋轉翼旋轉角速度繼續增加后，會導致輸入能量的增加，造成該主動控制方法成本的增加，因此可以認為ω=3.0 rad/s（T7）為最優的控制效果參數。

4.2 約化速度對立管結構渦激振動抑振的影響

由圖6可知，隨著約化速度（雷諾數）的增加，海洋立管本身的振幅會發生先增加后減小的變化趨勢，因此必須考慮約化速度對立管渦激振動控制效果的影響。同時，根據上節可知，T7（ω=3.0 rad/s）的控制效果最優，此節對比T1 和T7 立管的渦激振動響應隨約化速度的變化。圖8 所示為T1 和T7 的振幅比隨約化速度增加而發生變化的趨勢。由圖8可知：隨著約化速度的增加，旋轉翼始終具有較好的控制效果，振幅比降低明顯，振幅比控制在0.01以內。

圖7 海洋立管渦激振動響應與旋轉翼旋轉角速度的關系（Ur=4.5）Fig.7 The relationship between VIV responses of marine riser and rotating velocity of rotating wings

圖8 海洋立管渦激振動響應與約化速度的關系Fig.8 The relationship between VIV responses of marine riser and reduced velocity

4.3 尾流場分析

圖9所示為海洋立管T1的振幅比、升力變化曲線以及渦量云圖變化（Ur=4.5）。以T1、T3、T6和T7為例進行分析,圖10所示為振幅比曲線對比，圖11所示為渦量云圖對比（Ur=4.5）。

圖9 T1的振幅比、升力變化曲線以及渦量云圖變化（Ur=4.5）Fig.9 Amplitude ratio,lift curve and vortex nephograms of T1(Ur=4.5)

由圖9 可知，海洋立管渦激振動響應的振幅比變化與升力變化是同步的，升力驅動立管結構運動；當海流作用于海洋立管時，結構后方會有周期性脫落的漩渦產生，周期性脫落的漩渦會造成作用在結構上流體力發生周期性波動，周期性的脈動升力驅動立管結構周期性運動。

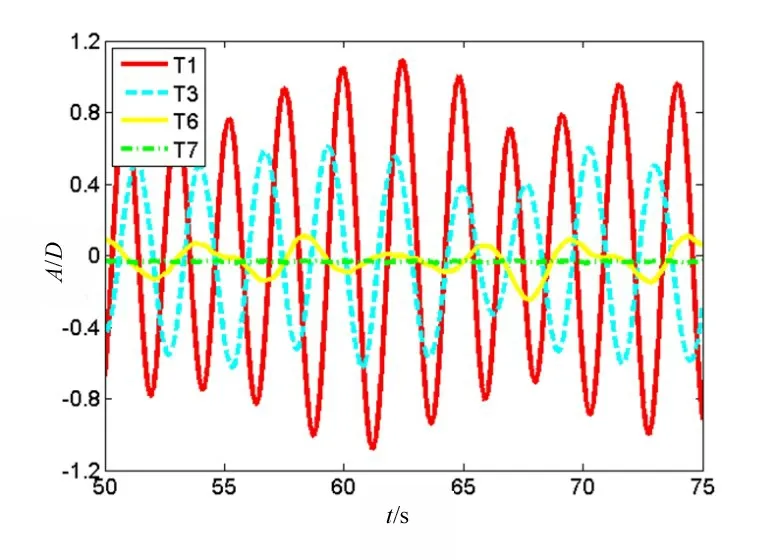
圖10 T1、T3、T6和T7的振幅比曲線對比（Ur=4.5）Fig.10 Comparison of amplitude ratios curves of T1,T3,T6 and T7(Ur=4.5)

由圖10可知，旋轉翼的旋轉運動會造成海洋立管渦激振動響應振幅比的降低；當ω=3.0 rad/s（T7）時，振幅的周期性波動幾乎趨于0，振動得到明顯的抑制，振幅比降低99.2%。

圖11 T1、T3、T6和T7的渦量云圖對比（Ur=4.5）Fig.11 Comparison of vortex nephograms of T1,T3,T6 and T7(Ur=4.5)

由圖11 可知，旋轉翼的旋轉運動會破壞海洋立管脫落的尾流漩渦，從而破壞海洋立管的周期性振動；當ω=3.0 rad/s（T7）時，尾流漩渦基本不再發生周期性脫落，渦激振動得到有效控制。

5 結 論

本文通過非定常流體數值計算方法求解分析了旋轉翼對海洋立管渦激振動的抑振作用，研究發現：

（1）隨著旋轉翼旋轉角速度的增加，立管的振幅比逐漸減小，最后基本不變，處于較低的振幅比狀態；當ω=3.0 rad/s 時，振幅比為0.008（Ur=4.5），抑制振動效果十分明顯；隨著旋轉翼旋轉角速度的增加，立管渦脫落的頻率比先減小，后趨于不變；當旋轉角速度大于2.0 rad/s時，頻率比開始迅速下降；當ω=3.0 rad/s時，頻率比接近于0，抑制渦脫落的效果十分顯著；

（2）當ω=3.0 rad/s 時，海洋立管渦激振動的抑振效果已經十分明顯，振幅比從0.98 下降到0.008，振幅比降低99.2%；當旋轉翼旋轉角速度繼續增加后，會導致輸入能量的增加，造成該主動控制方法成本的增加，因此可以認為ω=3.0 rad/s（T7）為最優的控制效果參數；

（3）隨著約化速度的增加，旋轉翼始終具有較好的控制效果（ω=3.0 rad/s），振幅比降低明顯，振幅比控制在0.01以內；

（4）海洋立管渦激振動響應的振幅比變化與升力變化是同步的，升力驅動立管結構運動；當海流作用于海洋立管時，結構后方會有周期性脫落的漩渦產生，周期性脫落的漩渦會造成作用在結構上流體力發生周期性波動，周期性的脈動升力驅動立管結構周期性運動。旋轉翼的旋轉運動會破壞海洋立管脫落的尾流漩渦，從而破壞海洋立管的周期性振動；當ω=3.0 rad/s（T7）時，尾流漩渦基本不再發生周期性脫落，渦激振動得到有效控制。