“圓” 來 如 此*
——芻談三角問題中“隱圓”的發掘策略

廣東省廣州市南武中學 (510240) 陳長定廣東省廣州市廣州開發區外國語學校 (510700) 蔡軍喜

我們常常會遇到一類解三角形問題，道是無“源”卻有圓.對于題目中顯然存在的圓，學生求解時大多困難不大，而對于部分題目中隱性存在的圓，如果不善于挖掘題中的隱含信息，將圓化“隱”為“顯”，則計算往往會非常繁冗，以致困難．構建將題目中的圓化“隱”為顯策略，將分散的信息集中于一個圓中，問題往往能夠化繁為簡、化難為易.下面筆者結合解三角形中部分高考及各地模擬考試中的典型試題，談談在三角形中將“隱圓”問題化“隱”為“顯”的常見類型和策略，供參考.

1 定長

我們知道，平面內到定點(圓心)的距離等于定長(半徑) 的點的軌跡是圓，因此有關涉及定(共)點、定長或等長的問題往往可以聯想構造輔助圓來解決．

例1 (2018六校聯考理科16題)在△ABC中，點D在邊BC上，DC=2BD,AB:AD:AC=3:k:1，則實數k的取值范圍為.

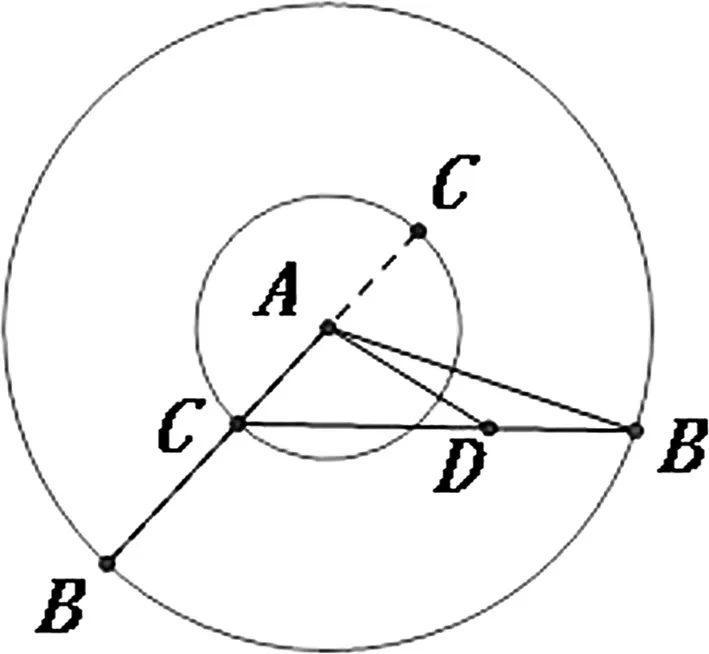
圖1

分析：觀察題目條件AB:AD:AC=3:k:1，即B,D,C三點到共點A的距離，聯想到圓的定義，以點A為圓心，分別以AB，AC長為半徑構造圓，再利用圓的有關性質解決.

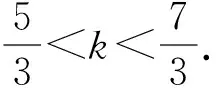
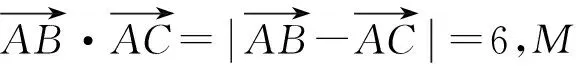
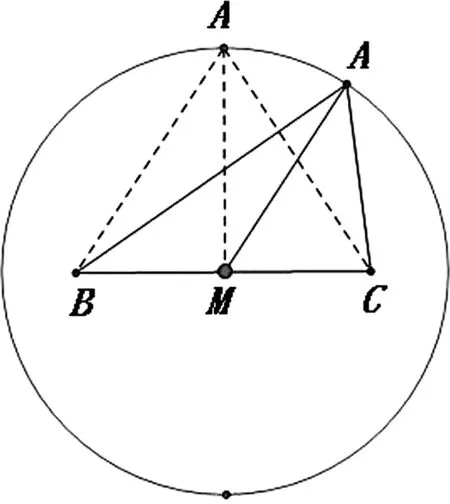
圖2

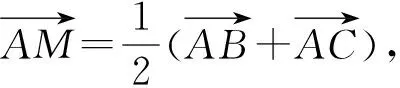
點評：當題目的條件中出現一個定點(或共點)，并能找到到這個定點(或共點)的距離等于定長的一些點時，常常可以根據圓的定義構造隱形圓，輔助解題.

2 定角

在同一個圓中，同弧所對的圓周角相等，相等的圓周角所對的弧長或弦長也相等.據此說明，若三角形的某邊及其對角確定(一邊一角)，則該邊所對的頂點必在其外接圓上運動．

例3 (2014全國卷Ⅰ理科16題)已知a,b,c分別為△ABC三個內角A,B,C的對邊，a=2，且(2+b)(sinA-sinB)=(c-b)sinC，則△ABC面積的最大值為.

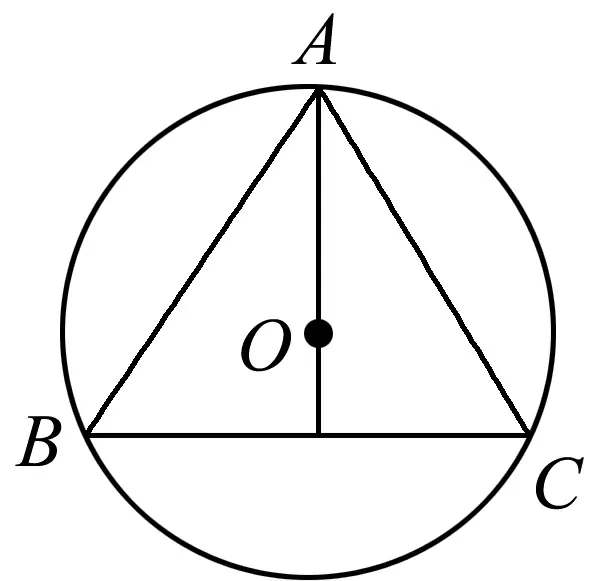
圖3

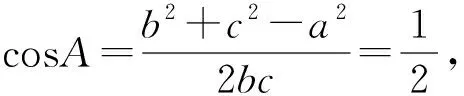
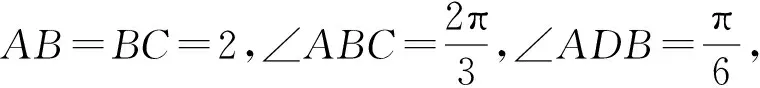
圖4

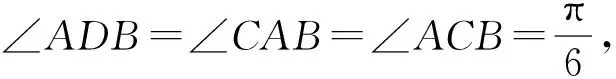
點評：當題目條件中出現定線段且這條線段所對張角恒為直角時，根據直徑對直角的性質可以這條定邊為直徑，作出隱形圓；當定線段所對的張角為非直角的定值時，利用三角形外心的性質，可確定輔助圓的半徑；當條件中有兩角相等，且這兩角對著同一條線段，且在這條線段的同側時，可將這條線段看作圓中的弦，這兩個等角看作圓中同弧(或弦)所對的圓周角，從而考慮構造隱形圓，輔助解題．

3 定比

一般地，平面內到兩定點A、B距離之比為常λ(λ≠1)的點P的集合是圓，此圓叫做阿波羅尼斯圓(通常也稱為圓的第二定義)(注：本性質教材以例題呈現).若題目中有關于比例關系之類的等量條件，在審題時可以利用“阿氏圓”的定義挖掘隱形圓，使問題迎刃而解．

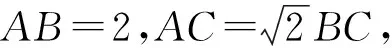
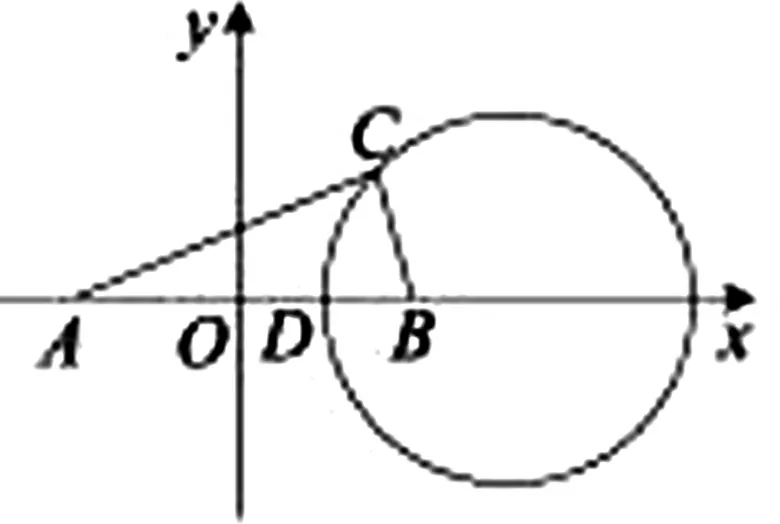
圖5

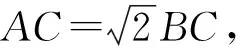
點評：本題借由阿波羅尼斯圓的定義，建立直角坐標系，找到點C所在的“隱形圓”，將求三角形面積的最大值問題轉化為求阿氏圓上的動點到線段AB的距離的最大值問題.

4 定平方和

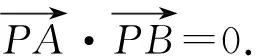
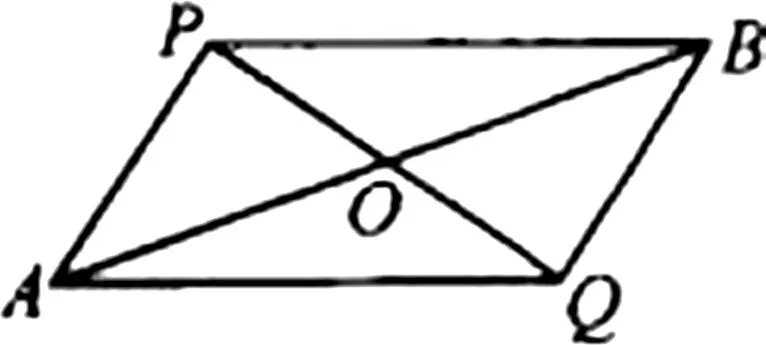
圖6

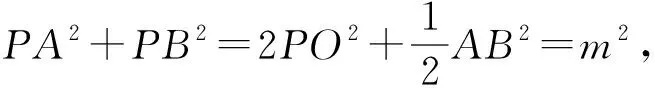
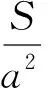
分析：本題用常規方法解答較困難.由平方和定值，可建立坐標系“發掘”“隱形圓”，以形助數來解決.

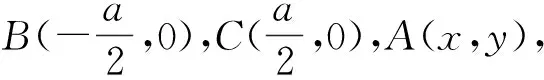
數學試題千變萬化．如果不對試題的共性進行研究進而形成共識，則不利于發展學生的數學思維，不能較好地培養學生的解題能力．以上主要闡述隱含圓的發掘及其在解題中的作用，所述例題的特點都是題設條件涉及一個或多個動點，結論則需要求某一條線段長度或角度的范圍或最值，從數的角度看，最終都要依靠函數、方程和不等式的知識來解決，且都有較大的運算量.這促使我們轉換解題的視角和入口．將“數”的問題轉化為“形”的問題，運用軌跡思想尋求動點的規律，從而發掘出“隱含圓”，進而獲得問題的優化解決方案，道是“無源”卻“有圓”.處理這類題目的關鍵在于能否把“隱形圓”“挖”出來，因此需要注意觀察、分析題目的結構特征，挖掘題目中的每一條信息，篩選出形成圓的關鍵或有用的信息，找準解題的切入點，讓其現出“圓”形，往往能使問題中隱晦不清的關系和性質在圓中清晰地展現出來，從而起到化隱為顯、化難為易的解題效果，這時你就會有“圓”來如此多嬌的美妙感覺.