一道高考含參恒成立問題求解的幾個角度*

新疆烏魯木齊市實驗學校 (830026) 符強如

縱觀近幾年的高考壓軸題，命題人比較熱衷偏愛于對導數知識的考查，其中求參數的取值范圍問題是重點考查的題型.其求解往往從分離變量法、直接討論法及圖像法三個角度去實施以2020年全國Ⅰ卷理數21題具體闡述筆者的思考.

1 問題呈現及背景

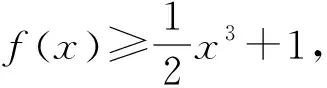
背景：這道題第(2)問從問題表述來看，傳承了全國卷高考命題樸實、簡約、穩健的風格.從函數的角度考察導數與含參不等式恒成立的綜合應用，而現階段以指數函數與三次函數為載體的導數與含參恒成立求解參數范圍問題，在高考壓軸題中頻繁出現，它不僅考查了考生的邏輯推理、數學建模、數學運算等核心素養，并對考生的思維能力要求較高，真正起到了壓軸的功能.

2 含參恒成立求解的多個視角

角度1 參變分離.若所求參數比較好分離時，學生普遍慣用分離變量法求解，這也是平時教學中講解思路及方向最多的.

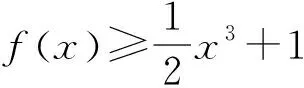
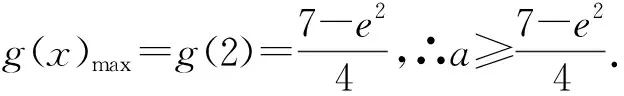
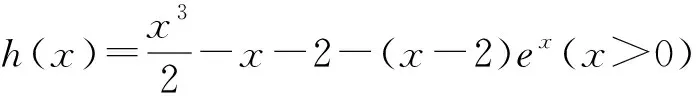
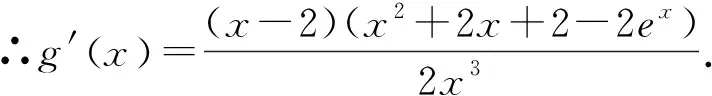
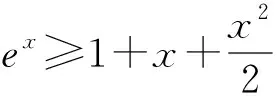
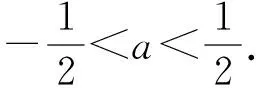
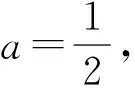
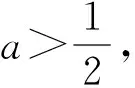
角度3 圖像結合.從圖像方向尋找突破點，找到兩個函數相切這一臨界位置，可以大大簡化運算.

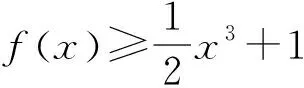
評注：不同的表征形式的求解著眼點就有不同，角度3需要敏銳的眼光，但有時具有一定的局限性.角度2通過變形后能較好找到分離討論的標準，一定要利用好端點.角度1較容易想到，但是需要較強的運算能力.

3 解題反思

數學知識體系中的各個知識點并不是孤立存在的，在各個知識之間存在一定的關聯，正因為數學知識之間的關聯，使我們可以從多個不同的角度來思考問題的解決策略，同時也最大程度地證明了數學思維的發散性.正如本題可以發現，含有參數恒成立問題可從以上幾個角度去求解，其求解思路切入各有其特征、使用的范圍和求解步驟.因求解的思路與著眼點也各不相同，所以表現出得解題過程難易程度就亦深亦淺.如，分離變量這一思路最易想到，也好操作，但是最后幾步需要較強的運算能力.又有時候這一思路有時需要多次求導，多次轉化.這樣經過多角度探究學生就能夠建立起相關知識體系，能夠以“一覽眾山”小的姿態來看待數學問題.作為教師唯有如此為學生的知識延伸和深度做指導，我們的復習才能真正優質高效，學生認知結構才能更加穩定，數學核心素養的培育才能更深入落實.