例析分段數列問題求解策略*

廣東省廣州市白云區教研院 (510440) 徐再友

近年來各類考試中出現了不少的分段數列問題，雖然與分段函數是不同類型的問題，但在結構上、問題的邏輯推理上有相近之處，需要我們根據分段函數求解思路，充分抓住數列問題的特點，使二者互幫互補、各用其長．本文列舉幾個典型例子并分析點評，主要提示一些常用有效的求解思路，希望對讀者朋友有所幫助．

一、尋找周期

例1 已知數列{an}滿足an+1=

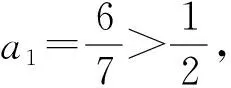
評注：本題通過賦值驗算，找出了數列的周期性，揭示了問題的實質，使問題輕松獲解，這是一類常見且比較簡單的問題．

二、建立聯系

評注：這是一個與分段函數中“取小”或“取大”函數是相似的，解題時要抓住數列中整數的特點，運用特殊值驗算，建立不等式即可范圍解決．

三、探求規律

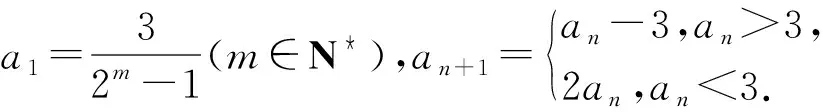
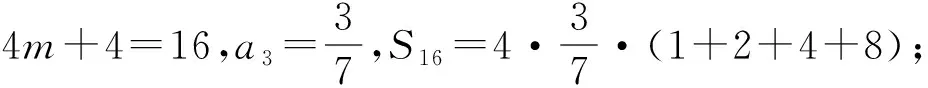
評注：抓住題目中求4m+4項和的特點，通過賦值驗算，找到了所求和式的規律，這是解題的關鍵所在．

四、活用遞推

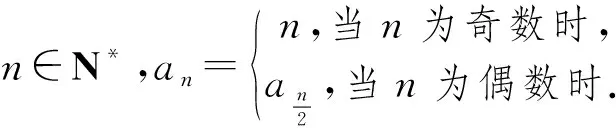
評注：在充分理解新定義的數列的實質的基礎上，根據定義規則進行賦值驗算，找出隱含的遞推關系，這是破解本題的核心步驟．

五、靈活替換

例5 已知f(x)是定義在正整數集N*上的函數,當x為奇數時f(x+1)-f(x)=1,當x為偶數時，f(x+1)-f(x)=3,且f(1)+f(2)=5,求f(x)的解析式.

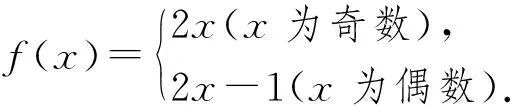
評注：本題是一個用函數符合表述的分段數列問題，通過分奇偶數討論并且及時替換，使問題獲得圓滿解決，這里的偶數時用奇數的情形進行替換是數列中常用的手段．

六、分類討論

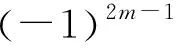
評注：在數列問題中，如果在已知式中含有(-1)n，則必須分奇數和偶數來討論，將結果表示成分段數列的形式，然后綜合其它條件繼續解題．

上面幾個例題是近幾年高考復習中常見的題型，也反映了高考題的命題趨勢，我們應該適應新情況，及時調整、充實課堂教學，給學生實時傳遞新方向，少讓學生走彎路．由于此類問題所給條件各異，很難有一個通法，因而在遇到具體題目時，應該抓住題目特點，注重分析，盡量展示出一個比較合理的解題方案．