一道圓錐曲線定值問題的探究與思考

江蘇省南京市棲霞中學 (210046) 劉建國

圓錐曲線的定值定點問題一直是高考考察的一個熱點與難點，多以壓軸題的形式呈現，此類問題多以考察學生的數學運算、直觀想象、邏輯推理能力等數學核心素養，教師在平時教學中，不僅僅是引導學生掌握定值問題的解法，更要注重對這類問題的本質進行梳理與探究(如文[1])，通過類比發散，在試題的剖析上更要有深度與廣度，引導學生在解題的基礎上對其進行深度學習與探究學習，找到解決問題的路徑與方法，在課堂中潛移默化的灌輸數學思想方法，培養學生的數學核心素養.筆者主要借助于2020北京卷中圓錐曲線定值問題，對其進行探究與類比，得出相應結論，展示探究這類問題的一般思路.

一、試題展示與解析

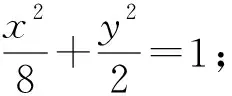
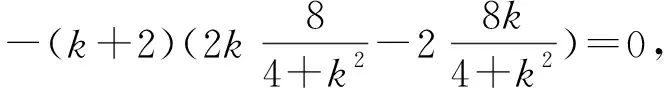
評注：本題以橢圓為載體，主要考察了定值問題，常用的技巧是“設而不求”的思想，通過數形結合與解析幾何的解題的通法解決問題，同時本題主要體現了數學運算、邏輯推理、直觀想象等數學核心素養的考察.

二、提煉結論

由2020年北京卷圓錐曲線的定值問題，通過對條件與結論的對比觀察，可以發現，點A的橫坐標與點B的更坐標的乘積恰好是a2，得到yP+yQ=0,那么對于更為一般的橢圓方程，如果滿足上述條件，則也具有相應的定值結論，如下所示：

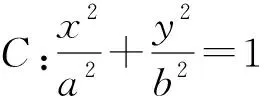
圖1

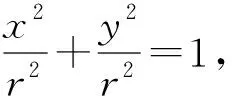
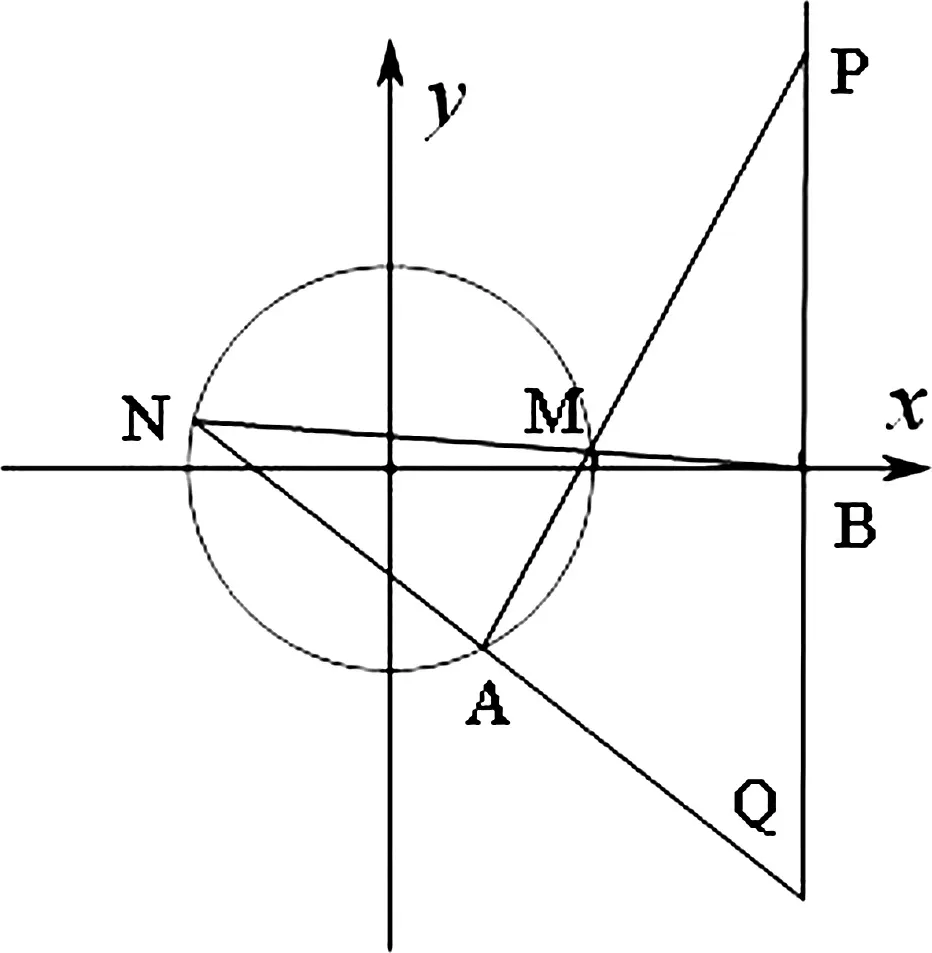
圖2

三、結論推廣

對于橢圓中有如上的定值結論，通過類比推理與邏輯推理，在圓錐曲線中的拋物線中也有類似的結論，如下：

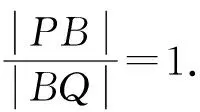
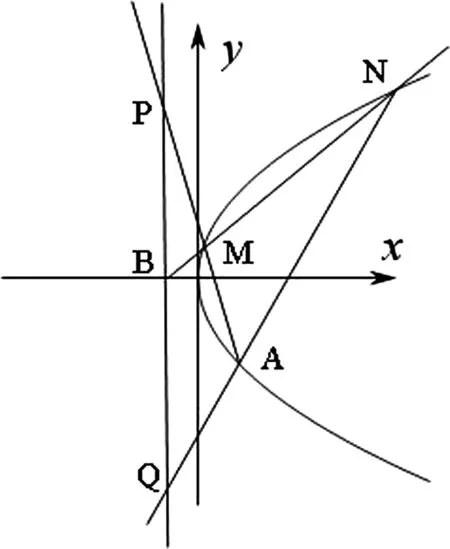
圖3

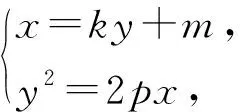
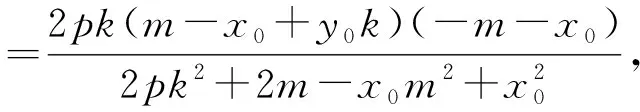
同樣在雙曲線中也有類似的結論，如下：

圖4

評注：本結論的證明過程與結論1的證明過程類似，這里不再贅述，有興趣的讀者可以仿照結論1進行證明.

四、幾點思考

1 深入探究題源，發揮高考題的功能

本文是以2020北京卷的圓錐曲線定值問題為載體，在解題過程中尋找條件與結論之間的關系，通過大膽猜想，小心驗證的方式得到結論1，圓錐曲線有很多類似的性質，這些都體現了圓錐曲線的內在統一的特征，這些內在統一的結論可以通過類比思想將知識由一種曲線遷移到不同的曲線中去進行探究其結論，這就要求教師在解題教學中要善于思考與引導，這樣有利于培養學生的邏輯推理與數學抽象等核心素養.因此，在平時備考過程中，教師有必要引導學生挖掘高考題的內涵與本質，而不是讓學生成為解題的工具，跳出題海，才能讓學生對數學產生興趣.

2 強化題后反思，引導學生思維遷移

圓錐曲線的定值問題往往具有代表性，引申性，教師教學過程中，注重題后的反思，在引導學生對問題進行探究過程中，應積極引導學生的類比聯想，讓學生不拘泥于一道題目的解答，引導學生掌握題目本質上的內涵，方可達到一道題解決一類題的效果，從一個問題到解決另一個問題上的思維上尋找共性，只有這樣，才能讓學生真正明白題目命制的背景，在解題思路的基礎上得到思維的發展，這就需要教師在引導學生探究這些結論時，應該注重學生思維的發展，加強學生能力的提升，重視數學核心素養的培養.

3 重視數學運算，培養學生運算能力

學習數學離不開數學與運算，不會算、一算就錯、有思路算不出結果是大多數考生備考中最常見的問題，究其原因是因為學生數學運算能力的欠缺，應該重視對數學運算的教學，引導學生對算理的選擇，幫助學生樹立在圓錐曲線問題上的信心.