幾道隔板法求不定方程正整數(shù)解的個數(shù)問題

福建省連江第一中學 (350500) 黃錦濤湖北師范大學數(shù)學與統(tǒng)計學院 (435002) 謝 濤

近日，筆者聽了一次組合的新授課，排列組合是高中學習階段的一個重要知識點，隔板法是處理排列組合問題的一個重要方法，在課上教師介紹了隔板法，并且出示了一道例題，如下.

例1 求不定方程x+y+z=10的正整數(shù)解的個數(shù).

剛出示這道題的時候，學生感到很疑惑：這與所學的組合到底有什么關系？這時教師給出引導：對于這個不定方程，可以換個角度看待，把其轉(zhuǎn)化為已經(jīng)學過的組合問題.具體如下：

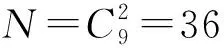
接著教師給出兩個變式：

變式1 求不定方程x+y+z=10的自然數(shù)解的個數(shù).

分析：變式1與例題十分相似，不同之處就是例題求的是正整數(shù)解的個數(shù)而變式1求的是自然數(shù)解的個數(shù)，既然是變式二者必然存在著某種聯(lián)系，如何把新的問題轉(zhuǎn)化為我們熟悉的問題即如何把求自然數(shù)解的個數(shù)轉(zhuǎn)化為求正整數(shù)解的個數(shù)是我們所要思考的.

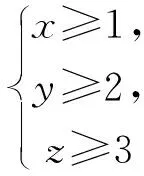
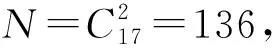
例2 (1)10個相同的球分給7個人，每人至少1個球，有多少種分法？

(2)10個相同的球分給7個人，有多少種分法？

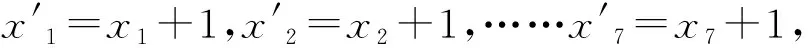
例1、變式1、變式2不僅開闊了學生的視野，而且對學生“轉(zhuǎn)化”思想的培養(yǎng)起到了很大的幫助，例2激發(fā)了學生利用隔板法處理實際生活問題的能力，數(shù)學題目是千變?nèi)f化的，要學會把新問題轉(zhuǎn)化為熟悉的舊問題去解決才能事半功倍.教師不僅要教會學生知識點，還要培養(yǎng)學生的數(shù)學思維，做到授之以漁.