激發學生空間想象能力的六個措施

云南省昆明市第一中學 (650000) 張遠雄

空間想象能力是對空間形式的觀察、分析、抽象的能力，主要表現為識圖、畫圖和對圖形的想象能力．識圖是指觀察、研究所給圖形中幾何元素之間的相互關系；畫圖是指將某些文字語言和符號語言轉化為圖形語言，以及對圖形添加輔助圖形、對圖形進行各種變換；對圖形的想象是指主要包括有圖想圖和無圖想圖兩種，是空間想象能力的高層次的標志．

《考試大綱》具體要求如下：能根據條件作出正確的圖形，根據圖形想象出直觀圖形；能正確的分析出圖形中的基本元素及相互關系；能對圖形進行分解、組合與變換；會運用圖形與圖表等手段形象的揭示問題的本質．回顧近幾年的高考試卷中關于立體幾何的考題，真實地反映出對考綱要求的知識點的全面考查，又有基礎知識的落實，更有能力考查的體現．

我們在復習備考中，必須精做題、練規范、廣看題、勤思考、善總結，做到熟悉各類題型的解法，完善各種題型的規范表述．下面就幾個重點題型舉例分析，供同學們參考．

一、通過識別三視圖考查組合體的面積與體積

例1 已知某幾何體的俯視圖是長為8，寬為6的矩形，正視圖是一個底邊長為8，高為4的等腰三角形，側視圖是一個底邊長為6，高為4的等腰三角形．

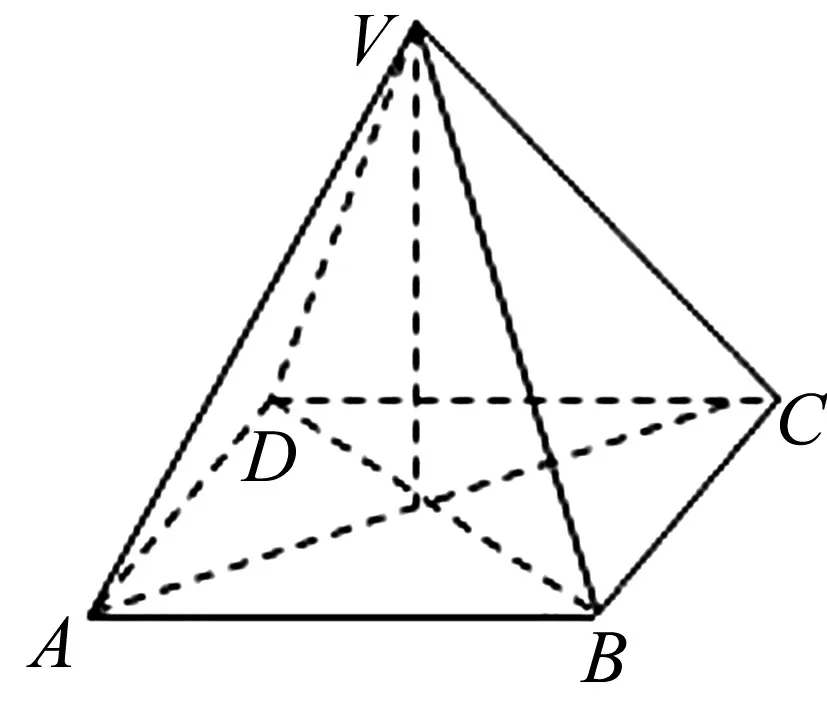
圖1

(1)求該幾何體的體積V；(2)求該幾何體的側面積S．

解析：由幾何體的俯視圖是長為8，寬為6的矩形，正視圖是一個底邊長為8，高為4的等腰三角形，側視圖是一個底邊長為6，高為4的等腰三角形．可得該幾何體是一個底面為矩形，高為4，頂點在底面的射影是矩形中心的四棱錐V-ABCD如圖1.

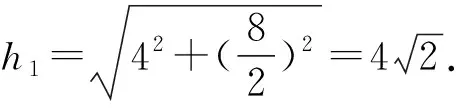
評注：給出幾何體的三視圖，考查幾何體的形狀、表面積、體積等問題，首先由三視圖找到原幾何體的相關數量，再運用面積公式和體積公式來解決問題，在計算錐體和臺體的側面積時，必須求出側面的斜高，應注意的是三視圖中側面的高是錐體和臺體的高，而不是斜高，不能混淆．

二、通過添加輔助線降低對幾何圖形的理解難度

例2 在三棱錐P-ABC中，D為AB的中點．(1)若與BC平行的平面PDE交AC于點E，如圖2求證：點E為AC的中點；(2)若PA=PB，且△PCD為銳角三角形，又平面PCD⊥平面ABC，求證：AB⊥PC．

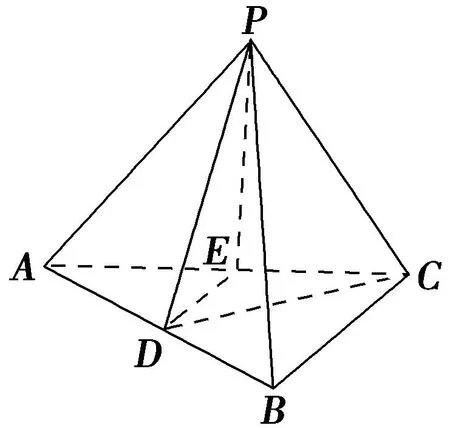
圖2

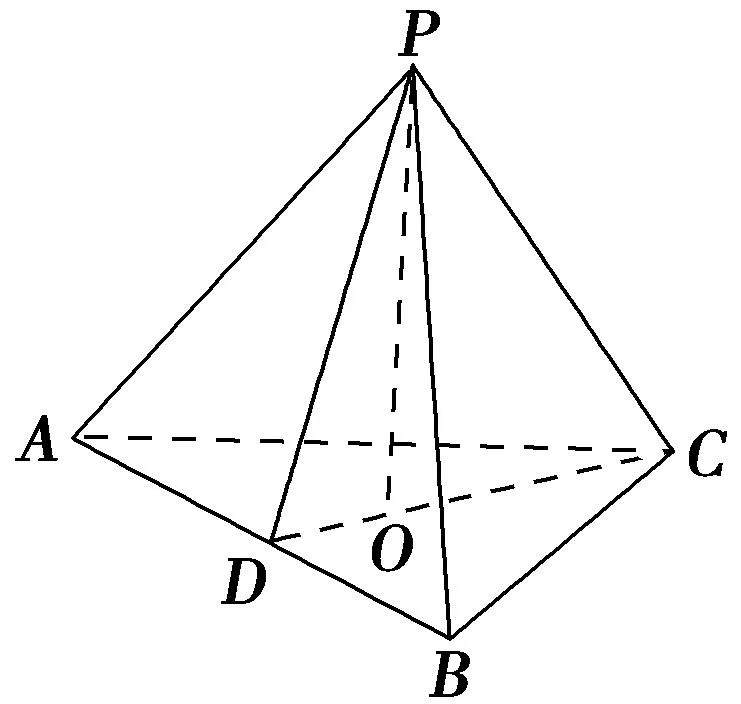
圖3

證明：(1)平面PDE交AC于點E，即平面PDE∩平面ABC=DE，而BC∥平面PDE，BC?平面ABC，所以BC∥DE． 在△ABC中，因為D為AB的中點，所以E為AC中點．

(2)因為PA=PB，D為AB的中點，所以AB⊥PD，因為平面PCD⊥平面ABC，平面PCD∩平面ABC=CD，在銳角△PCD所在平面內作PO⊥CD于點O，如圖3，則PO⊥平面ABC．因為AB?平面ABC，所以PO⊥AB，又PO∩PD=P，PO，PD?平面PCD，則AB⊥平面PCD，又PC?平面PCD，所以AB⊥PC．

評注：有一些題目中給出了某些條件，但這個條件的作用比較難發現，我們必須添加一些輔助圖形將條件細化，使這些條件在解題中能發揮作用．如本題中由面面垂直很難找到直線與平面垂直，我們就應該直接在一個平面內作交線的垂線，創造出直線與平面垂直．

三、運用空間向量解決幾何體中的角的問題

例3 如圖4，四棱錐P-ABCD中，底面ABCD為矩形，PA⊥底面ABCD，AP=AB=2，點E、F是棱AD、PC的中點，直線PC⊥平面BEF.求平面BEF與平面PAB夾角的大小．

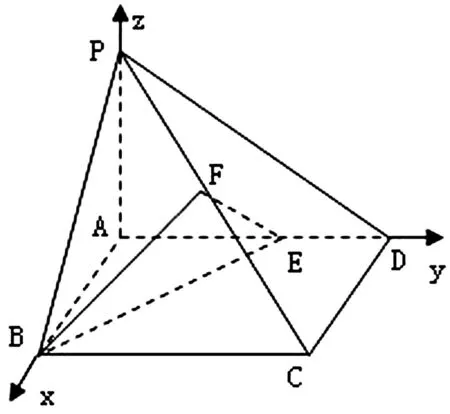
圖4

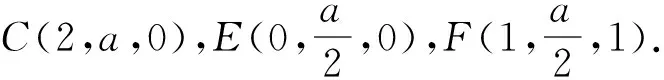
評注：空間向量是解決空間角問題的有力武器，同時也減弱了對空間幾何體抽象理解，本題抓住直線PC與平面BEF垂直，利用向量運算建立方程解決參數問題，這是用空間向量解題的優越之處．

四、抓住折疊中的不變量判斷新的線面關系

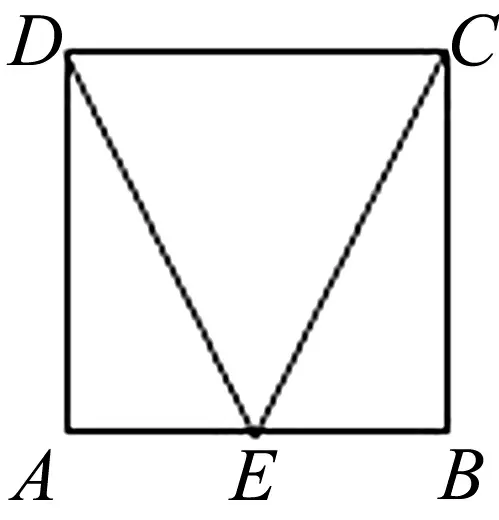
圖5

例4 如圖5，ABCD是正方形，E是AB的中點，將△ADE和△BEC沿DE和CE折起，使AE與BE重合，記A與B重合后的點為P，

(1)求證：PE⊥平面PDC； (2)求二面角P-CD-E的度數．

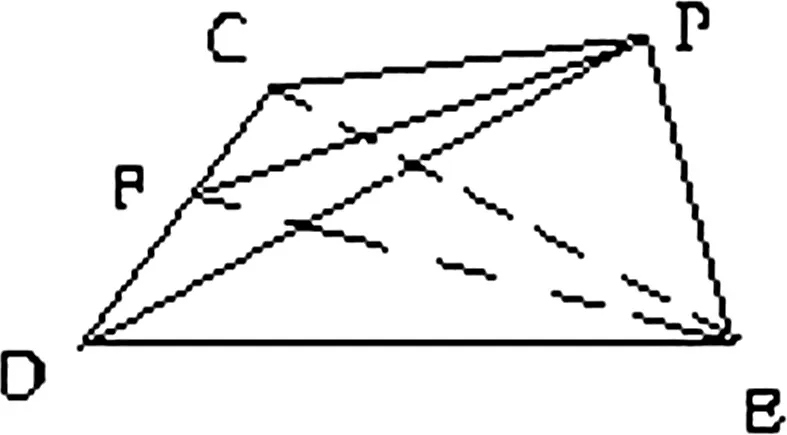
圖6

解析：從折疊的過程可以看出，AD⊥AE，EB⊥BC這兩個垂直關系是不變量，而折疊后A、B重合為P，故在立體圖6中有PE⊥PD，PE⊥PC，根據線面垂直的判定定理可獲解．

證明：(1)由折疊過程可知PE⊥PD，PE⊥PC，又PE∩PE=P，PD?平面PDC，PC?平面PDC，故PE⊥平面PDC．

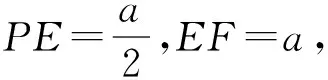
評注：折疊問題是比較常見的問題，弄清楚給出的已知條件的折疊前后的變化情況是解題的關鍵，本題中折疊前后的頂點位置和字母名稱都改變了，但垂直的關系沒有改變，抓住了這一點，就抓住了問題的實質．

五、關注一些立體幾何中的探索性問題

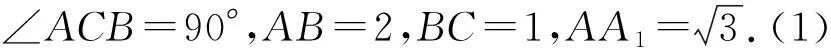
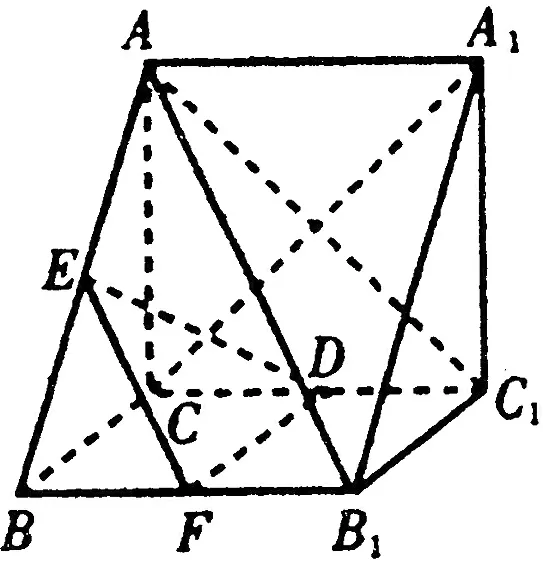
圖7

(2)當E為棱AB的中點時，DE∥平面AB1C1.如圖7，取BB1的中點F，連結EF，FD，DE，因為D、E、F分別為CC1、AB、BB1的中點，所以EF∥AB1，而AB1?平面AB1C1，EF?平面AB1C1，所以EF∥平面AB1C1；同理可證FE∥平面AB1C1，因為EF∩FD=F，所以平面EFD∥平面AB1C1，又DE?平面EFD，所以DE∥平面AB1C1．

評注：在解決存在性問題中，首先對一個判斷下結論，然后在設法證明你的結論的正確性．本題中證明直線與平面平行，常用的有兩種方法，即證明平面外一條直線與平面內一條直線平行，或證明直線所在的平面與要證的平面平行，而已知中點再找中點是最基本的思路．

六、了解立體幾何在實際生活中的的應用

例6 如圖8，邊長AC=3，BC=4，AB=5的三角形簡易遮陽棚，其中A、B是地面上南北方向兩個定點，正西方向射出的太陽光線與地面成30°角，試問：遮陽棚ABC與地面成多大角度時，才能使所遮影面ABD面積最大？最大面積是多少？

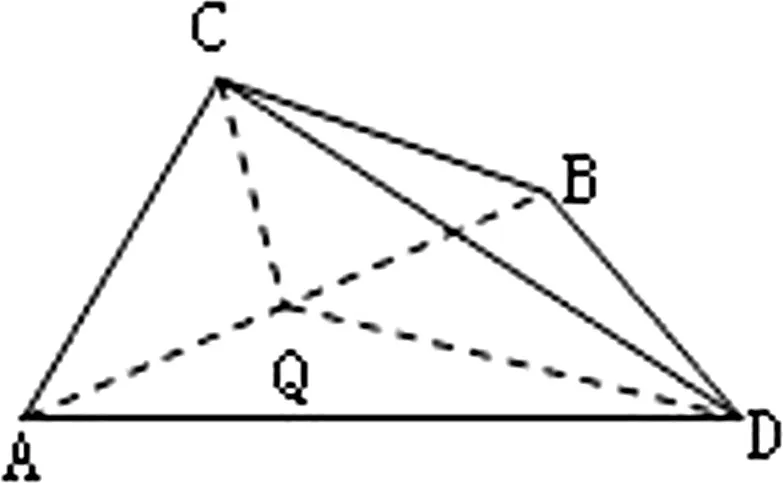
圖8

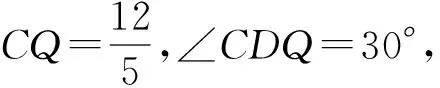
評注：立體幾何知識在實際生活中應用廣泛，解決這樣的問題首先需要將應用問題抽象為某一個類型的數學問題，本題是與立體幾何有關，然后在建立幾何模型，落實相關條件，找到它們之間的聯系，列出等式是解題的關鍵，平時要加強知識應用方面的訓練．