基于“三個理解” 促進深度學習

上海市復興高級中學 (200434) 方長林

發展學生核心素養已成為我國基礎教育改革的風向標，《普通高中數學課程標準(2017年)》提出了發展學生數學抽象、邏輯推理、數學建模、直觀想象、數學運算、數據分析六大學科核心素養.培育數學學科核心素養的關鍵是要促進學生的深度學習.所謂深度學習，就是指在教師引領下，學生圍繞著具有挑戰性的學習主題，全身心積極參與、體驗成功、獲得發展的有意義的學習過程[1].深度學習是以對學科本質和知識意義的滲透理解為基礎的探究型學習活動，需要學生對學習內容有深切的體驗和深入的思考，而不是學科知識的淺層化和學科思維的表層化.當然，有效促進學生深度學習的前提是要充分發揮教師的主導作用.理解數學、理解學生、理解教學的水平是教師專業水平和育人能力的集中表現，是構建深度學習數學課堂、促進學生深度學習的必要條件.理解數學，就是要高屋建瓴地把握數學內容的本質，站在系統的高度認識數學，特別是對數學內容所蘊含的數學思想和方法要有深入理解；理解學生，就是要全面了解學生的思維規律，把握學生的認知特點；理解教學，就是要把握教學的基本規律，按教學規律辦事[2].

1 理解數學，設計整體性的單元學習

深度學習的“深”體現在系統結構中.“單元”是知識結構化的重要表現，所以深度學習倡導單元學習.以往的數學教學，教師的著力點往往是單課教學，缺乏對教學內容的整體設計和結構化思考；對數學課堂學習活動的意義、作用關注不夠.單元學習設計，就是在單元整體內容中去把握相關的具體數學內容，更加重視數學學科內容本質的學習，更加關注數學學科核心素養的形成、核心能力的提升.開展單元學習設計，教師必須建立好數學學科核心素養與學科核心內容之間的關系，依據課標和教材，選擇單元學習主題、確定單元學習目標、設計單元學習問題、落實單元學習評價.

案例1 “三角函數”單元學習

第一環節：深度理解課程標準，確定單元學習目標

(1)理解任意角、象限角、弧度等概念，會進行弧度制與角度制的互化.

(2)理解任意角三角函數的定義.

(3)掌握同角三角函數的基本關系式和誘導公式.

(4)掌握三角函數的圖像和性質，體會三角函數是刻畫周期現象的重要數學模型.

(5)掌握和差角公式、二倍角公式.通過公式的推導，了解它們的內在聯系，提高邏輯推理能力，并利用這些公式進行恒等變形和解決有關計算問題，體會三角式變換的思想方法.

(6)掌握三角函數模型的簡單應用，培育數學運算、數學建模核心素養.

第二環節：搭建明晰思維導圖，統觀單元學習全局

(1)縱向結構思維導圖

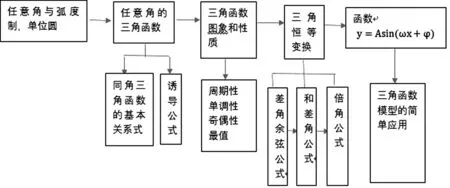
圖1

(2)橫向聯系思維導圖

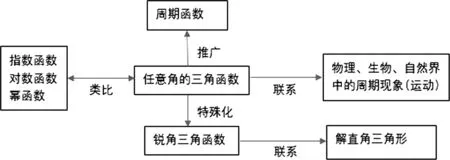
圖2

第三環節：設計問題驅動學習 構建單元知識網絡

(1) 為什么要學習三角函數？“任意角”的概念是怎樣獲得的？

(2) 弧度制的引入為三角函數的研究奠定了基礎，你能理解引入弧度制的必要性嗎？

(3) 三角函數是怎樣定義的？它與冪函數、指數函數、對數函數的定義相同點與不同點是什么？(數學抽象)

(4) 同角三角函數基本關系式和誘導公式由來你清楚嗎？公式的應用價值是什么?

(5) 三角函數圖像與性質的研究過程與方法你清楚嗎？(直觀想象)

(6) 兩角差的余弦公式不僅是和(差)角公式的基礎，也是誘導公式的一般化，你能畫一張三角公式的“邏輯結構圖”嗎？你能領悟這些公式的推導過程中用到了那些數學思想方法嗎？(邏輯推理、數學運算)

(7) 函數y=Asin(ωx+φ)(A>0,ω>0)是刻畫周期現象一個非常重要的函數模型，你能借助圖形計算器作出它的圖形嗎？知道參數A,ω,φ的物理意義嗎？知道參數A,ω,φ對函數圖像的影響嗎？

(8) 你能針對現實生活中的某種周期現象，用適當的方法搜集數據，處理數據，并利用這些數據為這種周期現象建立一個函數模型嗎[3]？(數據分析、數學建模)

單元學習，如果沒有問題意識，整個學習過程就變成了知識的記憶，也就成了一種淺層學習.利用有思維含量的問題驅動學習，問題引導、自主探究、解決問題，可以將零散的知識系統化，構建知識網絡，形成知識體系，凸顯學科大概念知識.同時在解決問題中，也有效地發展了學生的數學學科核心素養.

第四環節：設計多樣評價方式 聚焦單元目標達成

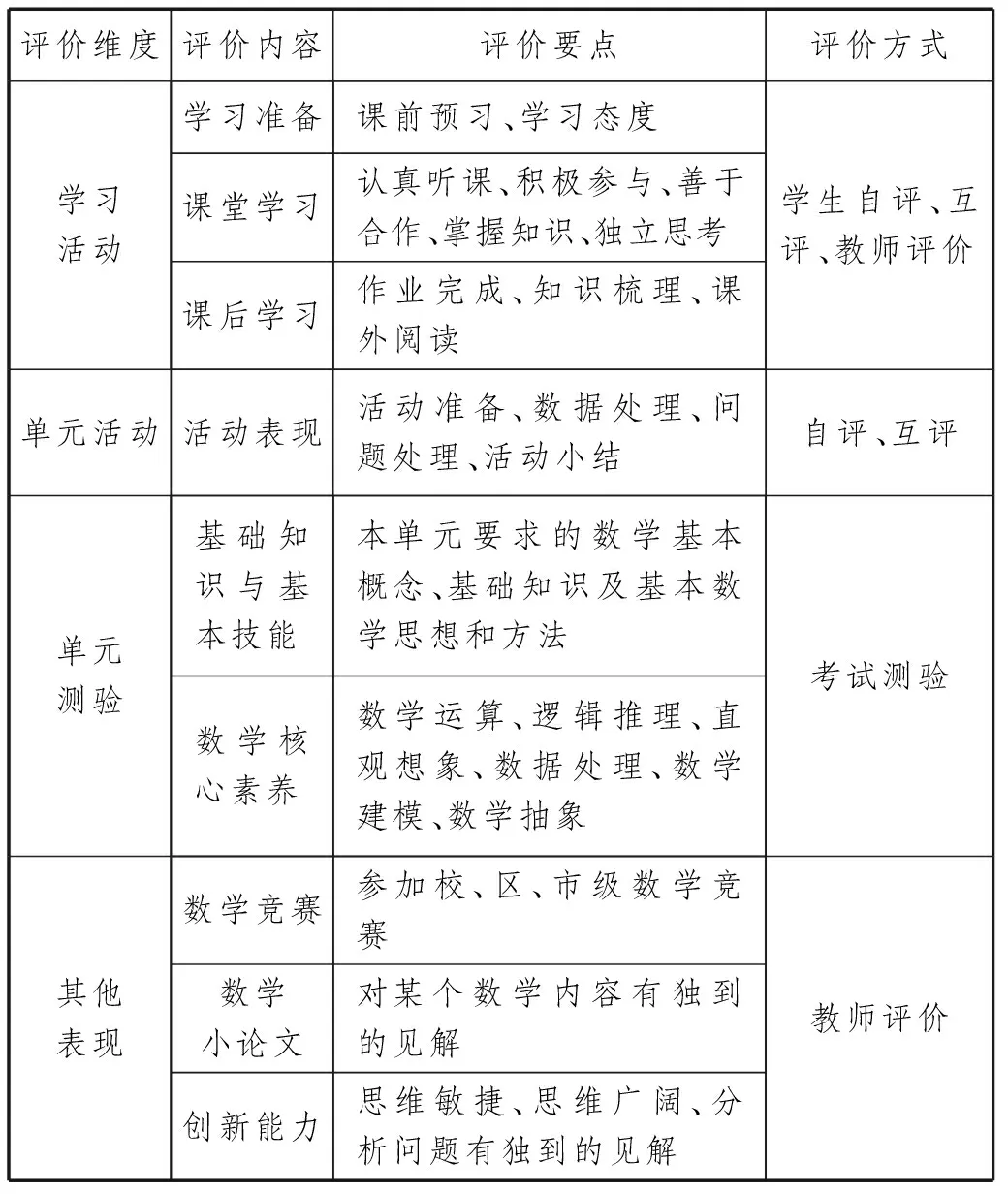
“三角函數”單元學習評價表[4]

公正客觀的數學單元學習評價，不僅成為促進學生學習改進的有效手段，而且能夠幫助學生認識自我，養成良好的學習態度和學習習慣，很好地促進學生的發展.

2 理解學生，設計梯度性的變式問題

深度學習的“深”體現在學生的認知規律中.深度學習是建立在學生已有知識的基礎上的概念改變，由易到難，由淺入深，循序漸進，它是一種理解性的學習，強調的是深層次的思考.

數學是思維的學科，數學概念是思維的細胞，數學從根本上說是“玩概念的”.促進學生的深度學習，要重視對“問題串”的設計.設計一系列相互“關聯”的“問題串”可以引導學生進行系統的、連續的思維活動[5].

在使用提升小波分解數控機床熱誤差數據后，采用最小二乘支持向量機(LSSVM)解決對每一層分解信號的訓練和預測問題。最小二乘支持向量機方法是采用最小二乘線性系統作為損失函數，代替傳統的支持向量機采用的二次規劃方法，簡化了計算復雜性的同時也可以保證預測結果的準確性[8]。而使用提升小波處理后的功率數據也更有規律，使用最小二乘支持向量機可以進一步提高預測精度。

案例2 “函數的概念”學習片斷

(1) 初、高中函數兩個定義的比較分析

初中的定義是“變量說”，易于理解；高中的定義是“集合-對應說”，比較抽象，學生難以理解.尤其定義中的函數定義域、值域、對應關系是函數作為數學模型時應關注的三個要素學生普遍感到理解起來有困難.

(2)構建函數的概念學習過程

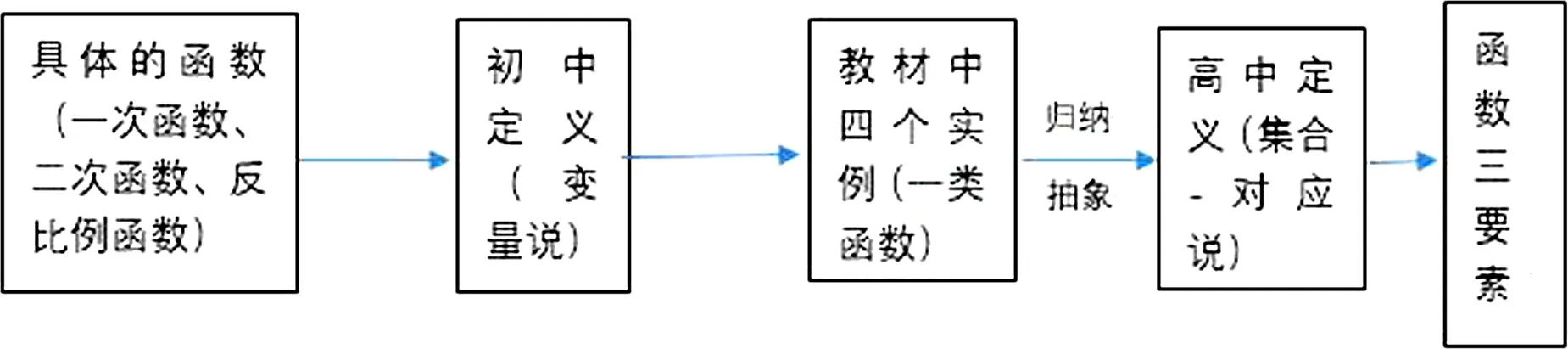
圖3

從認知角度分析，函數概念的學習經歷了由具體熟悉的函數到抽象的定義，再到具體實例，歸納，數學抽象，最后形成函數的概念.從學科育人的角度分析，函數概念的學習經歷了從數學知識(函數的定義、定義域、對應關系、值域)到數學思想方法(思想：函數；方法：比較、歸納、概括)，再到核心素養(數學抽象)不斷升華的過程.

(3)設計符合學生數學認知規律的問題串

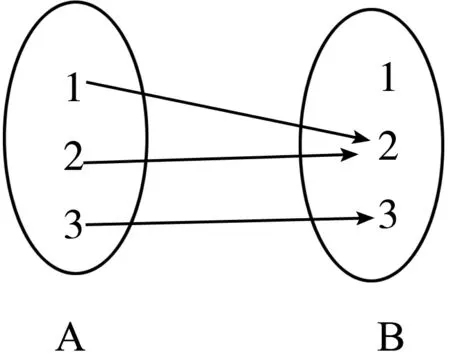
圖4

問題①集合A，B與對應關系f如圖4所示：f:A→B是否為從集合A到集合B的函數？如果是，那么定義域、值域與對應關系各是什么?

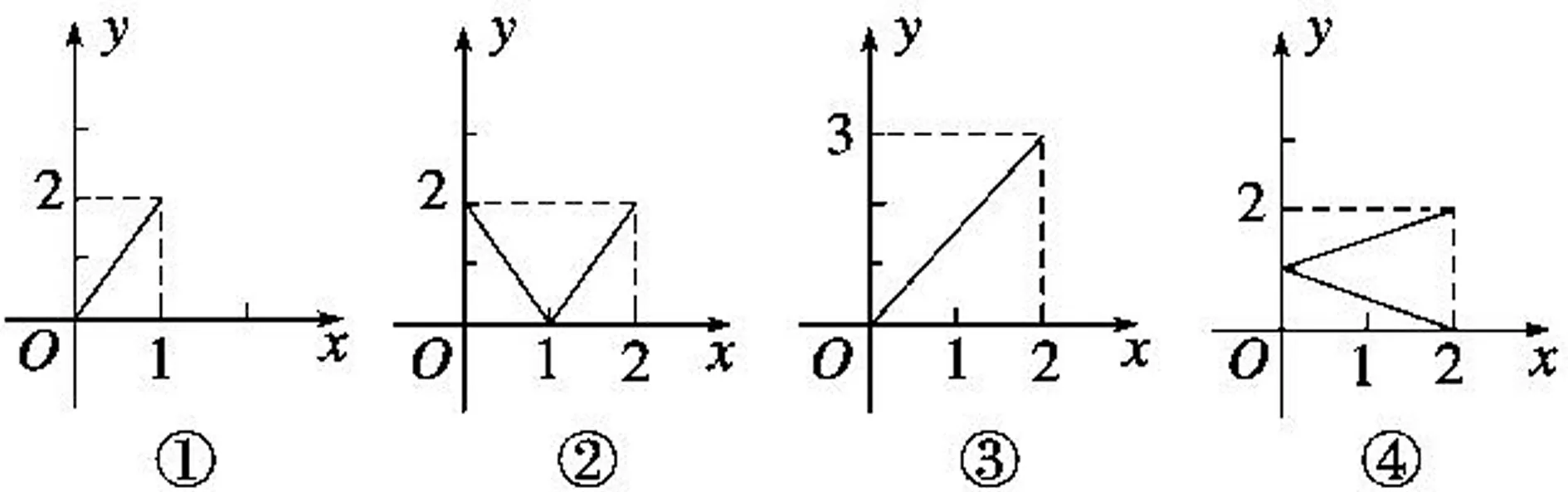
問題③設M={x|0≤x≤2}，N={y|0≤y≤3}，給出下列四個圖形，其中能表示從集合M到集合N的函數關系的是.(填序號).

問題④已知定義域為D的函數f(x)=x2,如果值域為A={4 ，9}，這樣的函數有多少個？

問題⑤已知函數f(x)的定義域D={1 ，2 ，3}，值域A?D且滿足f(f(x))=f(x)，這樣的函數f(x)有多少個？

問題⑥設D是含數1的有限實數集，f(x)是定義在D上的函數，若f(x)的圖像繞原點逆時針旋轉30°后與原圖像重合，則在以下各項中，f(1)的可能取值只能是( ).

設計意圖：問題①至⑥由易到難，層層遞進.問題①、②檢測用函數定義刻畫函數和函數三要素的基本認識，屬于基礎題，是水平一問題[6].問題③運用函數定義作判斷，同時需要數形結合，問題④給出對應關系和值域，對定義域的可能性進行分析，檢測對函數概念的深入理解，屬于中檔題，是水平二問題[6].問題⑤、⑥檢測對函數概念的深度理解，屬于難題，是水平三問題[6].伴隨著一系列問題的解決，學生的思維活動也必將由淺入深，真正實現數學概念理解性的深度學習.

3 理解教學，設計探究性的課堂活動

深度學習的“深”體現在數學教學規律中.數學教學的重心在于“學”，而非“教”.所以在數學教學活動中，教師的角色是引導者、合作者，教師要把教學活動的重心放在促進學生學會學習上，充分地發揮學生學習的主體作用.數學課堂活動設計的關鍵詞：問題情境-自主探究-合作交流-提煉結果.深度學習，需要設計探究性的課堂活動環節.

3.1 創設深度的問題情境，引發探究

案例3 “二分法”教學情境的設計

“二分法”比較常見的情境設計是“猜價格游戲”.的確“猜價格游戲”活動，學生很感興趣，能夠活躍課堂氣氛.但是這樣的情境與“二分法”的本質沒有關聯.情境活動中看不見：閉區間上連續函數、端點值異號、函數的零點、方程的根等等.情境與數學內容是兩張皮，僅僅是“一半一半又一半”與“二分法”在操作層面上有點相似.我們知道，“二分法”的教學內容蘊含著豐富的數學思想方法，“函數與方程”、“數形結合”、“近似逼近”、“一般與特殊”、“程序化的算法”等等.所以“二分法”教學情境的創設必須以數學內容的本質為依據，以引發學生思考為切入點，引導學生用數學的眼光看問題.

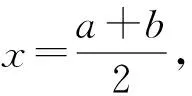
通過把“猜價格游戲”活動進行數學化提煉，學生在這個數學活動過程中，不僅學會了“二分法”，而且滲透了函數與方程、近似逼近、程序化算法等數學思想，更重要的是發展了學生數學建模、數學抽象、數學運算等數學學科核心素養.

3.2 進行深度的課堂對話，引導探究

深度學習需要通過課堂上師生深度的互動來實現，沒有有效互動性的數學課堂注定是傳授式的滿堂灌.傳統的數學課堂，教師是主體，教學的評價主要看授課內容的科學性、課堂組織的流暢性、教學語言的清晰性、板書設計的藝術性等.新課標下的數學課堂，學生是課堂的主人，教師是學生學習的同伴.課堂上的師生互動、生生互動、合作交流、自主探究構成了一道道亮麗的風景線.

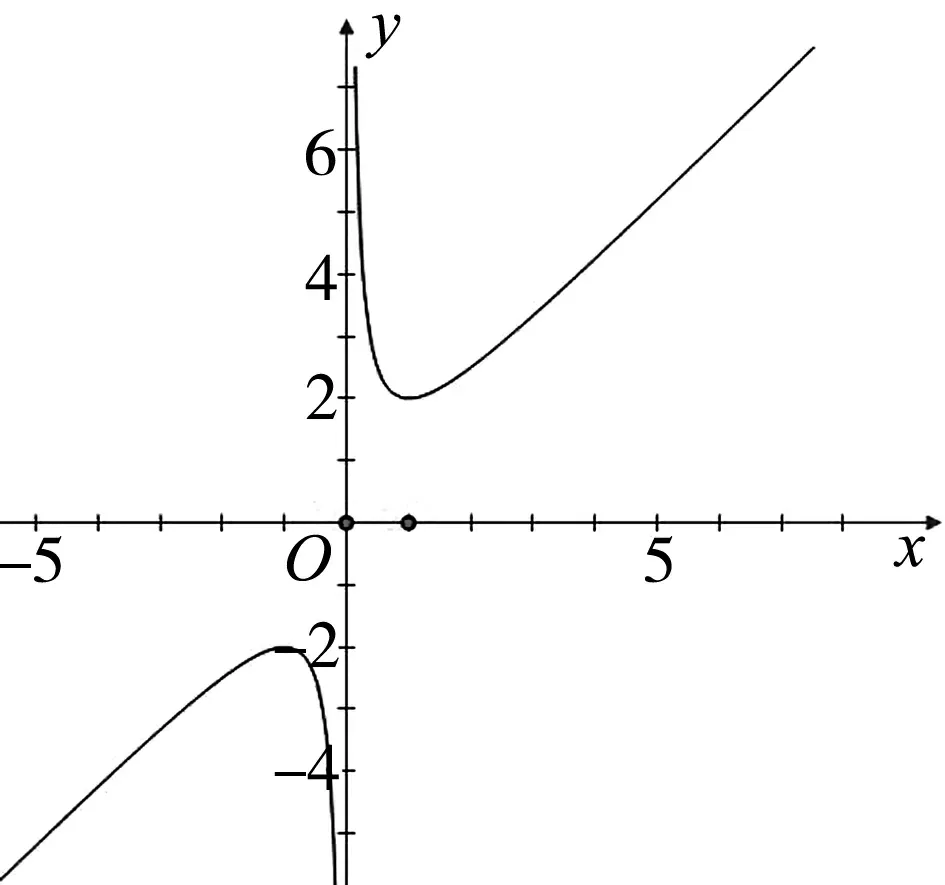
圖5

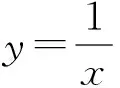
生1：研究的路徑是：圖像性質，即畫出函數圖像，觀察圖像，直觀描述圖像變化規律(圖形語言)；用自然語言描述函數性質(文字語言)；再用數學語言刻畫函數的性質(符號語言).

生2：主要研究函數的定義域、值域、單調性、最值、奇偶性等.

生3：描點作圖、圖像變換作圖(平移、對稱、翻折、伸縮)、圖形計算器作圖、幾何畫板軟件作圖等.

生5：描述性，如定義域、值域、奇偶性、單調性等.

生7：運用奇偶性定義f(-x)=-f(x)證明其為奇函數.

生8：運用單調性定義，結合奇偶性判斷其單調性.

4 結語

深度學習改變了傳統的傾聽、記憶、模仿和練習為主的復制型學習方式，轉變為以實踐、體驗、理解和遷移為典型特征的學習[1].促進學生的深度學習，對教師的素養提出了新的要求.需要教師勤于學習、勇于研究、敢于實踐，不斷提高“理解數學、理解學生、理解教學”的能力，改進教育教學方法，方可引領學生突破知識淺層化、思維表層化的學習，走進數學學科學習的深處，有效進行深度學習，孕育數學學科核心素養.