核心素養導向下數學運算能力的培養

錢桂榮 (江蘇省錫山高級中學 214174)

《普通高中數學課程標準(2017年版)》(下稱新課標)指出：數學運算與數學核心素養的其他五個要素構成一個有機整體，它們既相互獨立，又相互交融． 在數學運算核心素養的形成過程中，要使學生能夠理解運算對象，掌握運算法則，探究運算思路，選擇運算方法，設計運算程序，求得正確運算結果，以此進一步發展數學運算能力． 下面結合本人的教學實踐，談談尋求提升學生運算能力的途徑和方法．

1 明確運算對象，把握運算的指向性

新課標指出，數學運算是在明晰運算對象的基礎上進行的． 在課堂教學中，通過理解運算對象的內容、運算對象的背景、運算對象所在的知識體系，多角度觀察，實現運算對象的多元表征，并廣泛聯系相關知識，引導學生對已知與未知條件進行合理推斷，揭示因果關系 (由因導果或執果索因)，牢固掌握并靈活運用概念中所表現出的數量化、符號化的內涵，明確運算對象，把握運算的指向性．

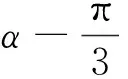
明確運算對象要求我們從多個視角審視運算對象：已知條件是什么？已知條件中的對象與所求對象有怎樣的聯系？從數量或圖形角度看，它們有何內在聯系？從數量的角度看，對應的數量、代數式、不等式、方程等是什么？從圖形的角度看，圖形由哪些基本的幾何元素組成，這些幾何元素之間有怎樣的位置和數量關系？這些問題在運算一開始都要考慮清楚，做到運算指向正確、任務明確．

2 準確運用運算法則，把握運算的合理性

數學運算最基本的要求是準確運算，提升運算能力的關鍵在于整體把握概念的實質、深刻揭示運算的本質，理解算理，遵循運算的基本法則．

本題容易采用下面的錯誤解法：

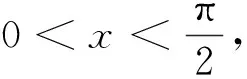
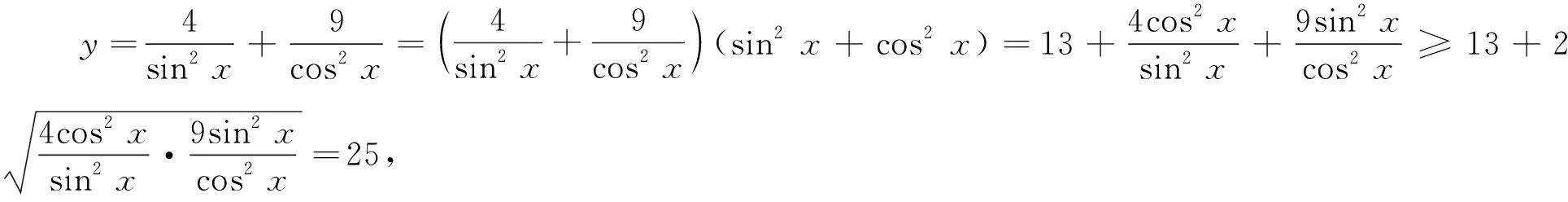
從上面例子可以看出，學生在運算中出現的錯誤從本質上說是對一些公式、定理、法則的本質掌握不夠清楚，要提高運算的準確性，必須狠抓算法、算理的正確使用， 避免盲目套用公式法則而導致解題失誤．

3 突出運算思路的尋找，把握運算的準確性

探究運算思路是在理解運算對象、運算法則的基礎上，確定運算的具體指向，尋求運算的條理和頭緒，是對數學運算的進一步推進． 運算思路合理與否，將決定運算的簡與繁，甚至成與敗，思路一旦確定，后面的工作便迎刃而解． 因此，探究運算思路是數學運算中的關鍵環節，通常也是最為困難的．

尋求運算思路時我們不妨可以借助波利亞的《怎樣解題》中提供的各種途徑：探尋包含在問題中的所有概念、公式、定理與方法，能不能利用它？聯想與現在的問題有關且已解決的問題，考慮能不能利用或模仿它？仔細推敲每個條件或努力挖掘出隱含條件，嘗試對問題進行轉化與化歸，正難則反． 如不能解決問題，能否找出一個更易著手的有關問題？一個更特殊的問題？一個類比的問題？一個更普遍的問題？

4 注重運算方法運用，把握運算的簡捷性

運算速度是運算能力的重要標志，在數學教學中要強調在準確運算的前提下算得快，而要想算得快，就必須做到基本運算熟練，運算方法合理，運算途徑簡便． 同一個問題往往可用不同的思路和方法去解決，方法選擇得越合理，運算速度也就會越快． 有些數學問題可根據題目的已知條件，利用有關概念、性質、法則進行簡化運算，從而提高運算速度．

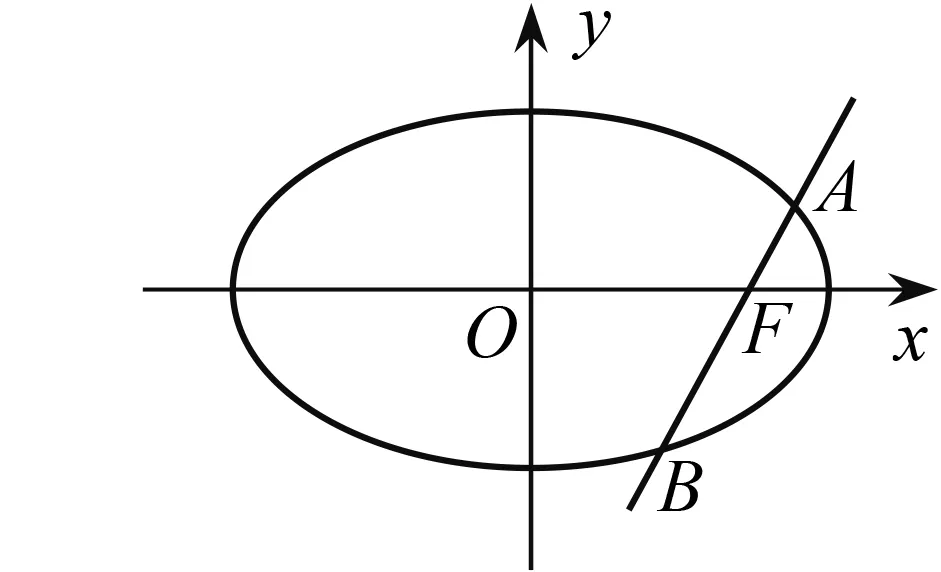
圖1

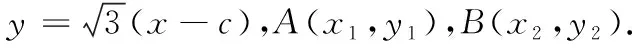
分析2 由于直線l過橢圓的右焦點，所以AF,BF都是橢圓的焦半徑，因此可以考慮用橢圓的第二定義，通過數形結合來求解．

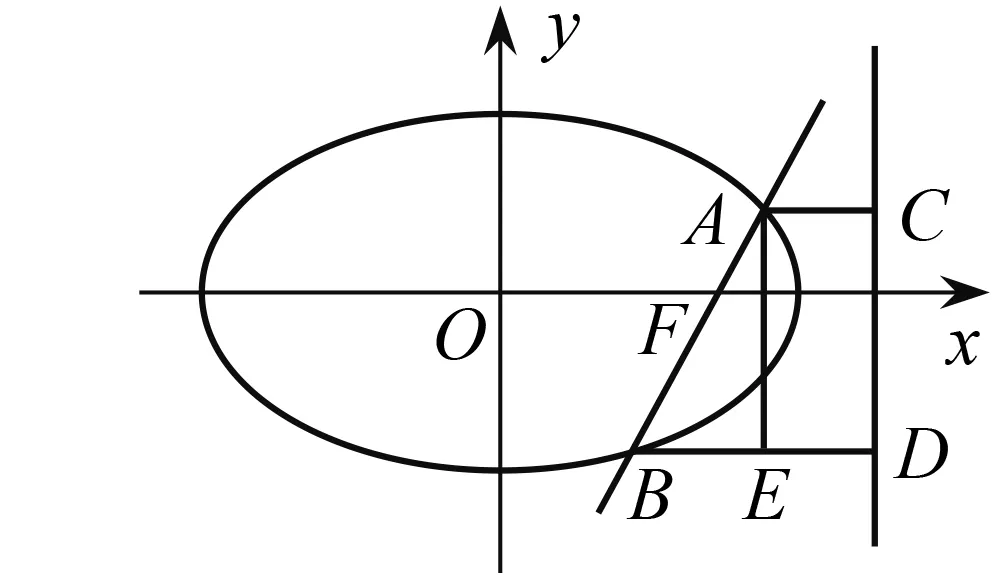
圖2

上面兩種解法中，第一種解法(即代數方法)是解決此類問題的通法，推理清晰嚴密，通過逐步消元求解，體現了解析幾何的一般解題方法，但這種方法有一定的運算量． 第二種解法(即幾何方法)，過程比較簡單，運算量很小，不易失誤． 然而當改變條件，直線不經過焦點，此時AF,BF不是焦半徑了，幾何方法就不適合了，只能用通法(代數方法)來求解．

5 講究運算的程序設計，把握運算的邏輯性

運算程序是對運算思路的具體落實，合理的運算程序設計是建立在對問題本質的思考之上的，它使運算按部就班地展開，易于駕馭，這對繁雜的運算尤為必要． 因此，應重視程序的設計，并相對“固化”一些常見且重要的運算程序，便于學生掌握．

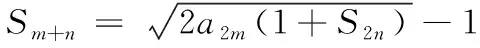
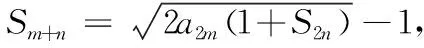
③-④，得an=(1+S2)qn-3(q-1)(n≥3)． 接下來只要求出q，即可得到數列{an}的通項公式，只需要再用賦值法求出前幾項即可．

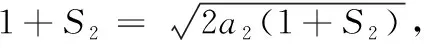
由⑤⑥得a3=4，a4=8，從而q=2． 所以an=(1+S2)qn-3(q-1)=2n-1(n≥3)． 由于a1=1，a2=2也滿足上式，故an=2n-1(n∈N*)．

在上述問題的解決過程中，先由條件對正整數m,n任意變化時，等式恒成立，可先固定一個量m，然后得出Sn+1與S2n關系，再由n和n-1對應的兩個等式成立，兩邊對應相除，得出{1+Sn}(n≥2)成等比數列，得到式子后再由an=Sn+1-Sn求得an(n≥3)關于n的關系式，最后對條件多次賦值求出數列前四項，這樣既求出了公比，也說明n=1，n=2時也滿足求出的當n≥3時的關系式，從而得到數列{an}的通項公式． 這些運算步驟都是數列問題的常用運算程序．

6 追求運算結果正確，把握運算的規范性

求得正確的運算結果，是進行數學運算的最終目的，處理不好，會前功盡棄． 運算技能必須通過長期的限時限量的訓練才能得到提高． 由于高中數學教學內容多、任務重，而一些“煩瑣”的運算很費時，在教學中教師要精心備課，在關鍵運算點上要舍得花時間，對求解過程中學生可能忽視的知識與方法、運算的程序與要點、或者可能產生的錯誤，以及計算時可能會遇到的障礙等，要進行全面的考察或預估，并在教學時重點加以關注． 在運算訓練中，應重點強調基本運算、規范運算，這是提高運算準確率的基礎. 在教學過程中充分讓學生參與一些數與式的運算過程，如在學習解不等式、三角恒等變換及圓錐曲線時，要有意識地安排一些運算量較大的問題，以培養學生不怕繁難運算的意志品質，并對典型的運算障礙與錯誤經常進行剖析，促使學生在經常性的運算過程中提高熟練程度和準確率．

運算能力不能脫離具體的數學知識而孤立存在，也不能離開其他核心素養而獨立發展． 它與觀察能力、記憶能力、表達能力、理解能力以及思維能力等諸多因素互相滲透、協調發展． 培養與提高學生的運算能力是一項復雜的系統工程，要貫穿于數學教學的始終，要有計劃、有目標、有意識地運用科學的方法進行長期的滲透和培養，使學生逐步領悟運算能力的實質，進而逐步提升思維能力和數學核心素養．