改進粒子群算法在移動機器人路徑規劃中的應用研究

孫 冬，趙開新

（河南工學院 計算機科學與技術學院，河南 新鄉 453003）

0 引言

目前常用的移動機器人路徑規劃方法主要有蟻群算法、神經網絡算法[1-2]、人工勢場法、遺傳算法、模擬退火算法、粒子群算法等[3-4]。與其他算法相比，粒子群算法具有參數設置少、實現簡單等優點[5-6]。但粒子群算法本身還存在著一些缺陷，如收斂速度慢、有早熟現象等，目前對粒子群算法的改進有基于動態調整慣性權重和基于收縮因子兩種方法，但大多改進算法不能突破經典慣性權重呈線性遞減的約束，粒子不能根據自我的位置動態調整對局部和全局信息的依賴度，導致粒子群算法效率低和次優路徑的產生。文獻[7]針對粒子收斂速度慢、搜索精度不高和算法性能過度依賴參數的選取等缺點，提出了一種非線性指數慣性權重粒子優化算法，使算法根據粒子最大、適應度值最小的指數函數更新慣性權重，突破了經典慣性權重呈線性遞減的約束，該算法有利于粒子在尋優過程中跳出局部最優，使粒子較快地收斂到全局最優位置，但是算法收斂時迭代次數過多。本文通過優化粒子群算法的權重系數來動態調整粒子群算法的全局和局部搜索能力，通過優化學習因子來動態調整粒子對自我和群體的依賴程度，減少算法收斂時的迭代次數，并將改進后的粒子群算法應用到移動機器人路徑規劃中，引導機器人快速高效地尋找全局最優路徑。

1 粒子群算法

粒子群算法（Particle swarm optimization algorithm, PSO）是根據鳥群的捕食和返巢活動提出的一種啟發式算法[8]，可設置數學模型的過程如下：搜索空間為D維，種群粒子個數為N，各粒子在D維空間上第t次迭代后位置為每個粒子的速度為其中i[1,m]，通過公式（1）和（2）來更新各粒子的速度和位置。

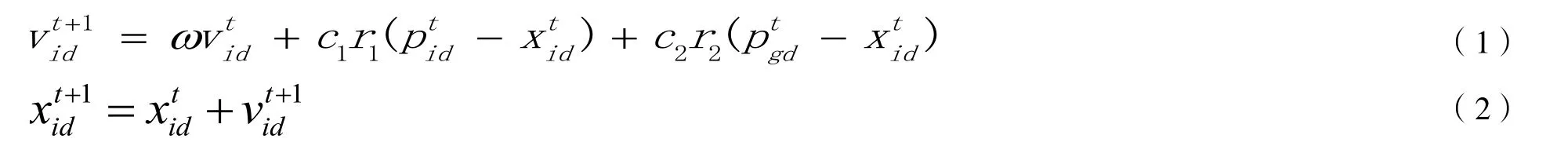
公式（1）中c1為個人認知因子，c2為社會認知因子，為權重系數，表示粒子個體位置最優解，表示粒子群體位置最優解,r1和r2為介于0 和1 之間的兩個隨機數。

在粒子群算法中，個體位置最優解按公式（3）進行更新，群體位置最優解按公式（4）進行更新[9-10]。

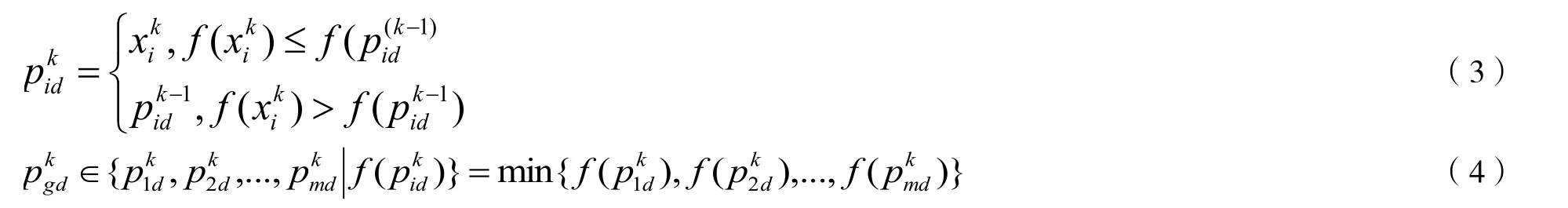
2 粒子群算法的改進

在粒子群算法中，權重系數的值是恒定的，粒子不會根據自我位置的優劣來動態調整下一次迭代的速度和位置；個人認知因子1c和社會認知因子2c不會隨著時間的推移動態調整下一次迭代的速度和位置，因此會導致算法局部收斂和收斂精度低的現象，本文通過動態調整權重系數和動態調整學習因子兩個方面對粒子群算法進行改進。

2.1 動態調整權重系數

優化后的權重系數值由公式（5）得出。

式（5）中，i為第i個粒子在第t次迭代的慣性系數值，max_iter為第i個粒子的最大迭代次數，min和max分別為第i個粒子慣性系數的最小值和最大值，粒子i的適應度值為fi，當前粒子群適應度的平均值為favg、最小值為fmin。

2.2 動態調整學習因子

在粒子群算法中，個人認知因子1c和社會認知因子2c不會隨著時間的推移動態調整下一次迭代的速度和位置，改進后的個人認知因子由式（6）得出，社會認知因子由式（7）得出。

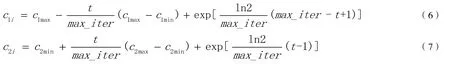
式（6）中1ic介于c1max和c1min之間，為粒子的動態個人認知因子，2ic介于c2max和c2min之間，為粒子群的動態社會認知因子。從式（6）可以看出，隨著時間的推移，1ic的值逐漸減小；從式（7）看出，隨著時間的推移，2ic的值逐漸增大。

從改進后的個人認知因子和社會認知因子的算式可以看出，在搜索開始時，粒子的自我學習能力比較弱、向社會群體學習能力比較強，全局搜索能力比較強，保持了種群的多樣性；在搜索將要結束時粒子的自我學習能力比較強、向社會群體學習能力比較弱，因此具有較強的局部搜索能力，從而提高了搜索的效率和精度。調整粒子群算法的權重系數和學習因子后粒子速度更新公式為（8）。

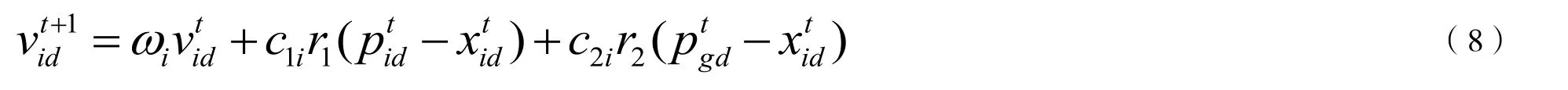
3 改進后粒子群算法在移動機器人路徑規劃中的應用

3.1 算法步驟

移動機器人路徑規劃的目的就是從初始節點到目標節點找到一條無碰撞的距離最短路徑，而粒子群算法正是解決粒子從起始點到終點的最優路徑問題，把改進后的粒子群算法應用到移動機器人路徑規劃中，可以協助機器人快速高效地搜索最優路徑。具體步驟如下：

步驟1：設置機器人運動的初始環境，初始化粒子速度、位置等參數。

步驟2：通過適應度函數計算粒子群中各粒子適應度的值。

步驟3：由公式（3）更新粒子個體最優值，根據公式（4）更新種群最優值。

步驟4：由公式（5）求出該粒子權重系數的值。

步驟5：根據時間t和粒子自我因子的最大、最小值，由公式（6）求解個人認知因子的值。

步驟6：根據時間t和社會認知因子的最大最小值，由公式（7）求解社會認知因子的值。

步驟7：由公式（8）更新粒子的速度，由公式（2）更新粒子的位置。

步驟8：當達到算法結束的條件則終止搜索，否則轉到步驟2 繼續執行。

3.2 仿真實驗

3.2.1 實驗環境及參數

用 MATLAB 構建柵格環境的仿真平臺如圖1 所示，障礙物分布在已知的全局靜態10×10 的柵格矩陣中并用黑色填充單元格表示。設置機器人起點坐標為S(0，0)，終點坐標為E（10,10）。粒子群算法中種群規模為100，粒子維數為10，迭代次數為40，權重系數最大值max 為0.9，權重系數最小值min 為0.4，個人認知因子最大值c1max為1.2，個人認知因子最小值c1min為0.6，社會認知因子最大值c2max為1.2，社會認知因子最小值c2min為0.6。在上述環境中分別采用粒子群算法PSO、文獻[7]粒子群算法EIW-PSO 和本文改進的粒子群算法進行機器人路徑規劃。

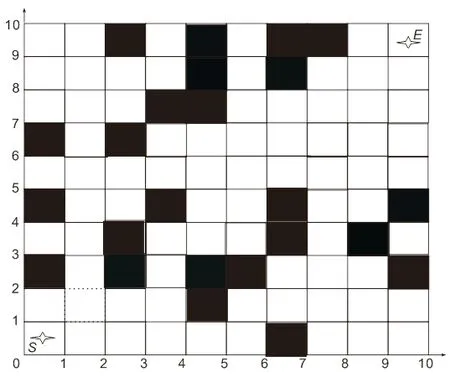
圖1 仿真柵格圖

3.2.2 實驗結果及分析

采用三種不同的算法進行移動機器人路徑規劃后仿真結果如圖2 所示，可以看出本文算法搜索到的路徑最短。各路徑的詳細距離長度如表1 所示，可以看出，在同一仿真環境下，采用粒子群算法求得的路徑長度為18.4275，距離平均值為18.7543；采用EIW-PSO 算法求得的路徑長度為17.8562，距離平均值為18.1278；采用本文改進的粒子群算法求得的路徑長度為15.2471，距離平均值為16.6827；采用本文優化后的算法所得到的路徑長度和距離平均值均比粒子群算法和文獻[7]粒子群算法EIW-PSO 有了明顯縮短。

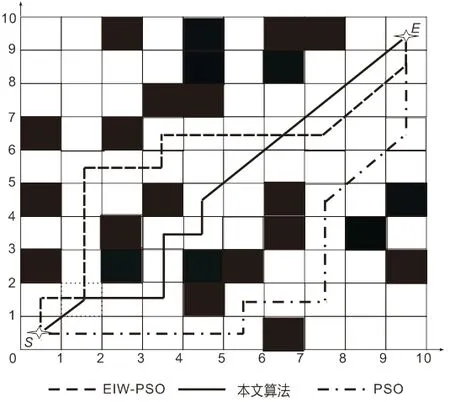
圖2 三種算法的路徑規劃對比

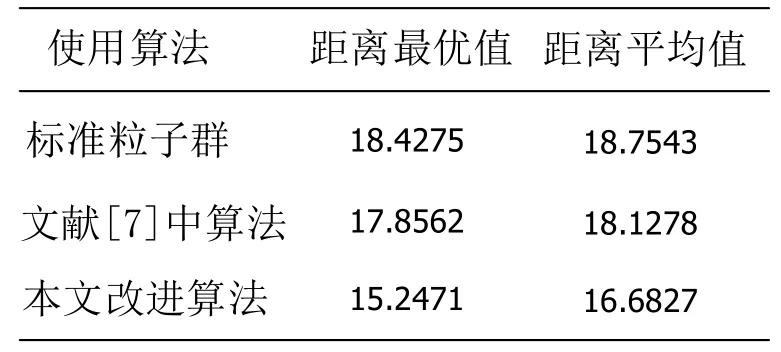
表1 三種算法的路徑長度比較

三種算法找到路徑所需要的迭代次數如圖3 所示，可以看出采用本文改進的粒子群算法進行路徑規劃，當算法收斂時迭代次數明顯小于粒子群算法PSO 和文獻[7]粒子群算法EIW-PS0。算法收斂后，本文算法在相同的迭代次數下粒子適應度值最小。這正是由于通過優化粒子群算法的權重系數和學習因子后，搜索前期增強全局搜索能力，并增強了自我學習能力；搜索后期加大局部搜索能力，增強了向群體學習能力。仿真結果表明，應用本文算法進行路徑搜索提高了搜索效率，加快了收斂速度。

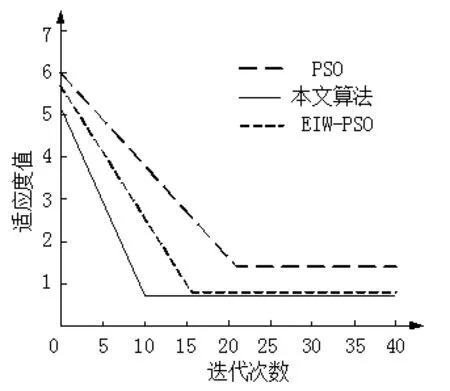
圖3 三種算法迭代次數比較

4 結語

隨著智能機器人技術的快速發展，路徑規劃問題逐漸成為國內外許多學者研究的熱點。本文從權重系數和學習因子兩個方面對粒子群算法進行改進，改進的算法突破了經典慣性權重呈線性遞減的約束，提高了收斂速度。把改進的粒子群算法應用在移動機器人路徑規劃中，結果表明該算法具有一定的優勢，對未來移動機器人路徑規劃有一定的指導意義。