基于有限元法和田口方法的翼子板成形工藝參數優化

王 興，吳明明，王江龍

（1.安徽三聯學院 機械工程學院，安徽 合肥 230601；2.合肥工業大學 機械工程學院，安徽 合肥 230009）

沖壓成形受材料、模具設計、沖壓設備等多因素的影響，會出現褶皺、破裂、拉毛、回彈等不同類型的成形缺陷。汽車前翼子板作為典型的沖壓成型薄板零件，最大變薄率和最大增厚率是其評價目標，必須綜合考慮，找出最優工藝參數組合，以保證零件成形質量。

對于沖壓成形最大變薄率和最大增厚率的控制，國內外學者均有深入研究。文獻[1]運用Dynaform 軟件對翼子板的沖壓成形進行了數值模擬，通過仿真得出汽車翼子板成形工藝及相應的優化方案。文獻[2]利用田口方法，采用正交試驗設計，就模具參數的穩健設計進行了分析。文獻[3]采用基于有限元的田口方法確定不銹鋼拉深成形過程中的工藝參數最優值，并找到這些參數對成形質量的影響。文獻[4]通過Minitab 軟件對沖壓件各參數進行分析，利用穩健性設計原理找出最佳沖壓方案再進行仿真試驗。文獻[5]利用田口方法結合Design-Exprt 軟件對后圍板沖壓參數進行多目標優化，將最優工藝參數組合進行仿真驗證，結果可以指導實際生產。

近年來，多種商用計算機仿真分析軟件應用于塑性成形加工領域，為沖壓加工的工程實際研究提供了有效保障，但是研究內容多集中在單一成形目標上。本文結合有限元法和田口方法，以某汽車翼子板沖壓件為研究對象，依據目標函數和約束函數，通過尋找信噪比最大值確定最優參數組合，獲得與實物成形一致性高的有限元仿真模型。

1 仿真試驗設計

1.1 有限元建模

以某型轎車前翼子板拉深成形為研究對象，通過零件模型的中性面偏置產生凹凸模，再產生壓邊圈。沖壓設備采用單動拉延機。圖1 所示為翼子板有限元分析模型。

經調研企業的生產實際情況，選取板材DC04，板厚0.7mm，材料的力學性能見表1。

1.2 田口試驗設計

考慮到多目標優化的需要，即兼顧最大變薄率和最大增厚率的雙重影響，本研究設定最大變薄率和最大增厚率所占權重各為50%，作為綜合評價指標考察翼子板的成形質量[6]。

依據板料成形過程中工藝參數對成形質量影響程度，選取試驗因素為凹模圓角半徑（A）、模具間隙（B）、摩擦系數（C）和壓邊力（D），考察目標為最大變薄率和最大增厚率。因素及水平取值見表2，表中t為板料厚度。

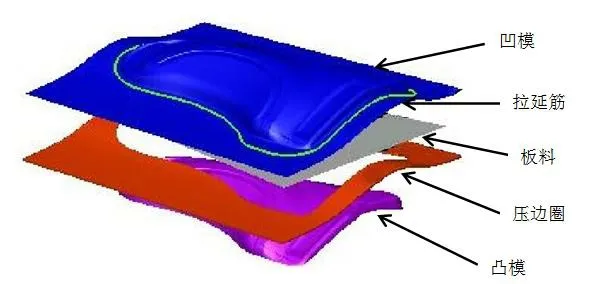
圖1 翼子板有限元分析模型

表1 材料力學性能

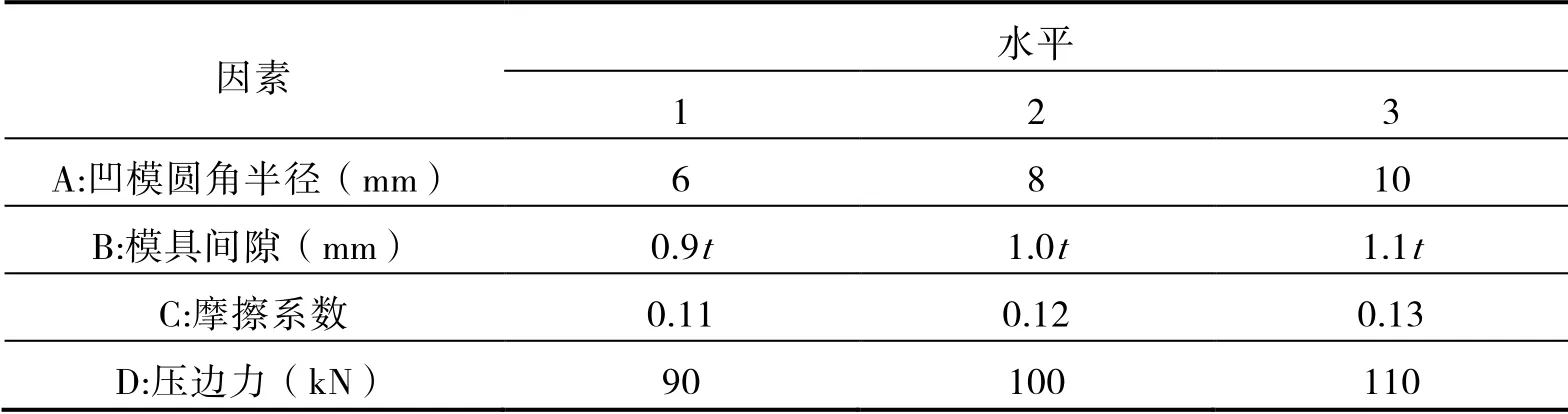
表2 因素及水平表

利用田口試驗設計原理，選取正交試驗表L9(34)，根據試驗參數確定試驗組數。翼子板的沖壓成形仿真數值模擬正交試驗記錄見表3。

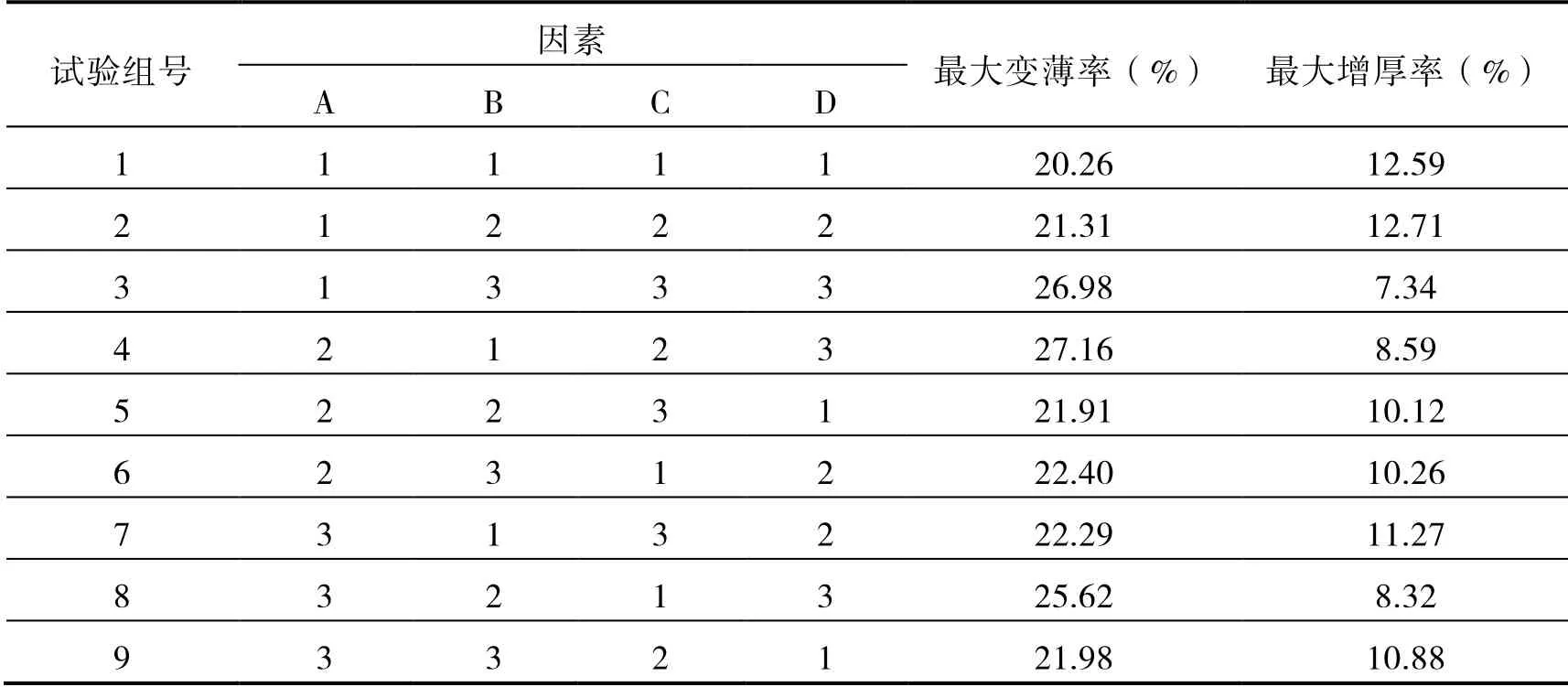
表3 翼子板的正交試驗記錄

2 結果與分析

2.1 試驗結果描述

因田口試驗中存在不穩定因素，多次試驗所得的結果會存在偏差，故采用信噪比作為試驗穩定性的評價標準[5]。信噪比是信號S和噪聲N的比值，其計算方法如公式（1）所示。對于覆蓋件的起皺和開裂現象，考察目標是最大增厚率和最大變薄率。在實際沖壓工程中，希望它們的值在合理范圍內越小越好，最大增厚率最好為零[6]，在田口試驗中，這種情況稱為望小值特性。從公式（1）可以看出信噪比是一個減函數，即信噪比的最大值對應目標的最小值。信噪比是田口試驗中評判試驗效果的重要依據。

式中：yi為第i次試驗的結果，n為試驗的次數。

綜合信噪比S/N為：

2.2 信噪比分析

依據本文的優化目標，要求切邊線內區域最大變薄率應小于30%，且越小越好；切邊線內區域最大增厚率應不大于10%，且越小越好。

優化的目標：最大變薄率取極小值，最大增厚率取極小值。

約束的目標：最大變薄率<30%，最大增厚率<10%。

本試驗利用Minitab 軟件處理數據結果，并根據分析結果選擇最優方案。信噪比計算結果見表4。

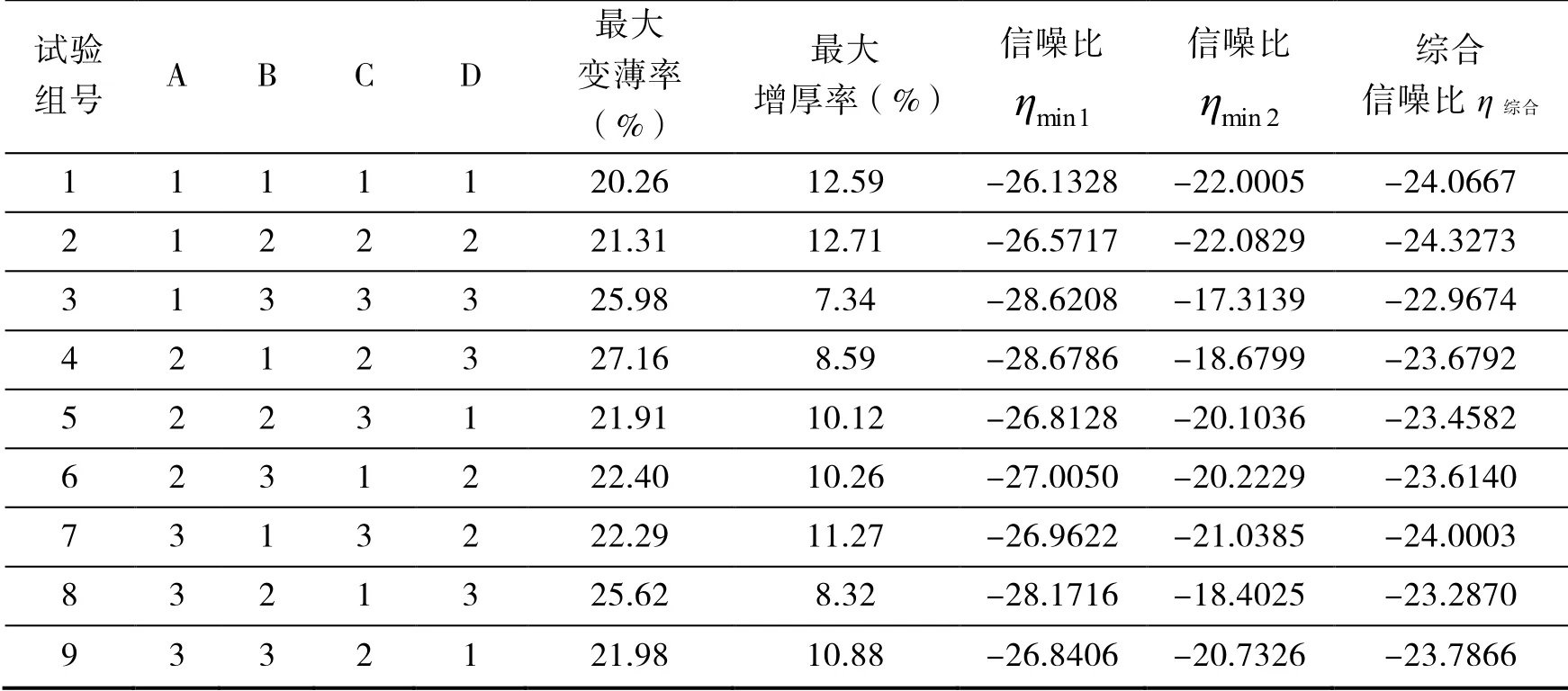
表4 信噪比計算結果

從表4 中可以看出，第3、4、8 組試驗均滿足優化目標函數的取值范圍。而更高的信噪比意味著更好的質量特性，因此，最佳工藝參數組合對應最大信噪比。從綜合信噪比計算結果表中可以觀察出，第3 組試驗的信噪比數值最大，為-22.9674，對應的最優參數組合為A1B3C3D3。即凹模圓角半徑6mm、模具間隙0.77mm、摩擦系數0.13 和壓邊力110kN 時為最優的工藝組合，最大變薄率為25.98%，最大增厚率為7.34%，此時翼子板成形質量最佳。

采用上述分析得到的最優參數組合進行沖壓成形，仿真模擬結果如圖2 所示。通過成形極限圖中的數據和模型，發現整體沖壓模擬情況較好，盡管壓料面上起皺，甚至強度不足，但是零件表面基本無缺陷，絕大多數位置處于臨界區之下，可以順利成形。只有左上角折彎處局部處于臨界區，有破裂可能，但是該區域在激光切割線之外，所以不影響零件最終的沖壓質量。另外，變薄率太低，零件就會剛度不足；變薄率太厚，容易產生堆積。從圖3 可以看出，在零件邊緣及中間區域選取7 個變薄率變化較大的特征點，獲得對應的變薄率數值。發現零件上只有邊緣及尾部少許部分變薄率超過了20%，而激光切割線以內零件區域的變薄率都不超過10%。同時，在最優成形工藝參數組合下，翼子板的最大變薄率和最大增厚率都符合工藝要求，制件成形質量在最大變薄率和最大增厚率之間取得了較好的平衡，可見優化組合的參數是合理的[7]。

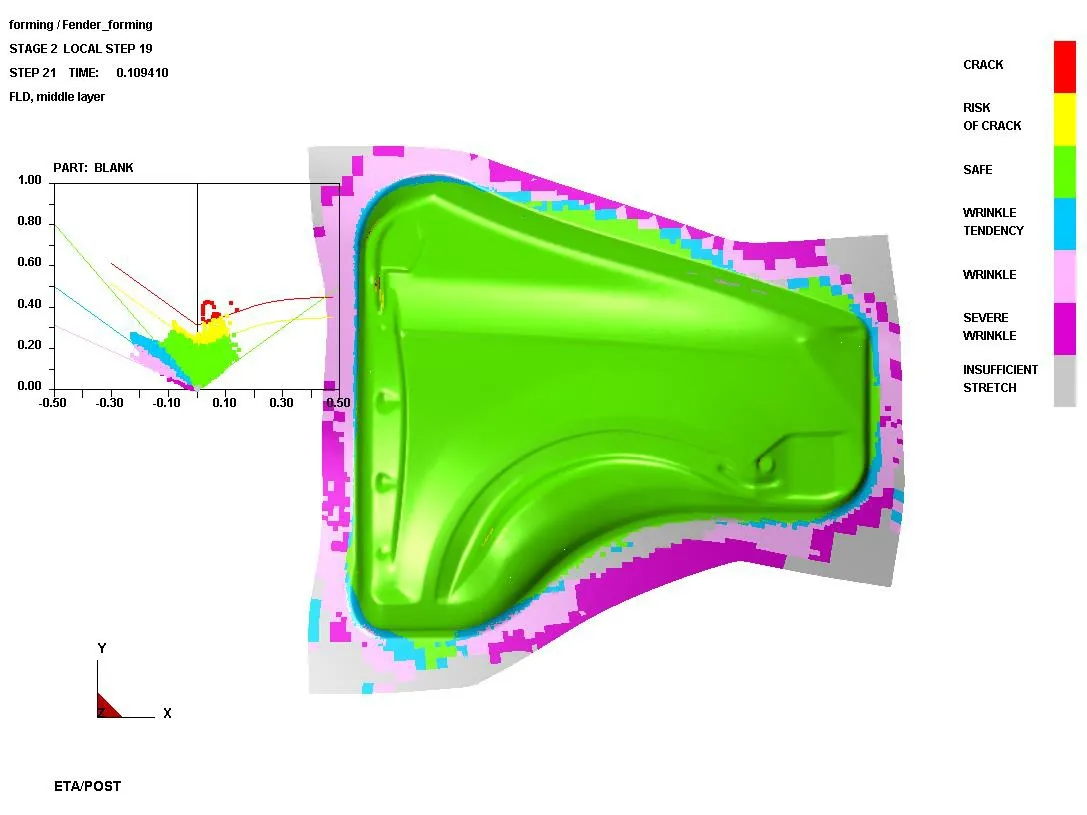
圖2 汽車翼子板成形極限圖

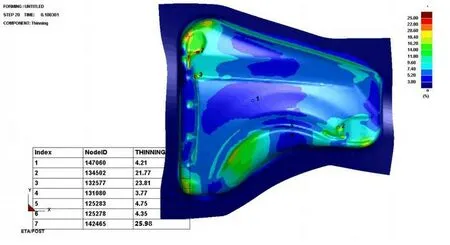
圖3 汽車翼子板變薄率分布圖

（1）依據優化目標對零件表面最大變薄率的要求是取極小值，分析試驗因素對最大變薄率的影響程度，通過信噪比響應表5 中的極差排秩可以快速確認因素影響從大到小依次是D、A、C、B。即壓邊力的影響最大，其他因素影響程度都很小。

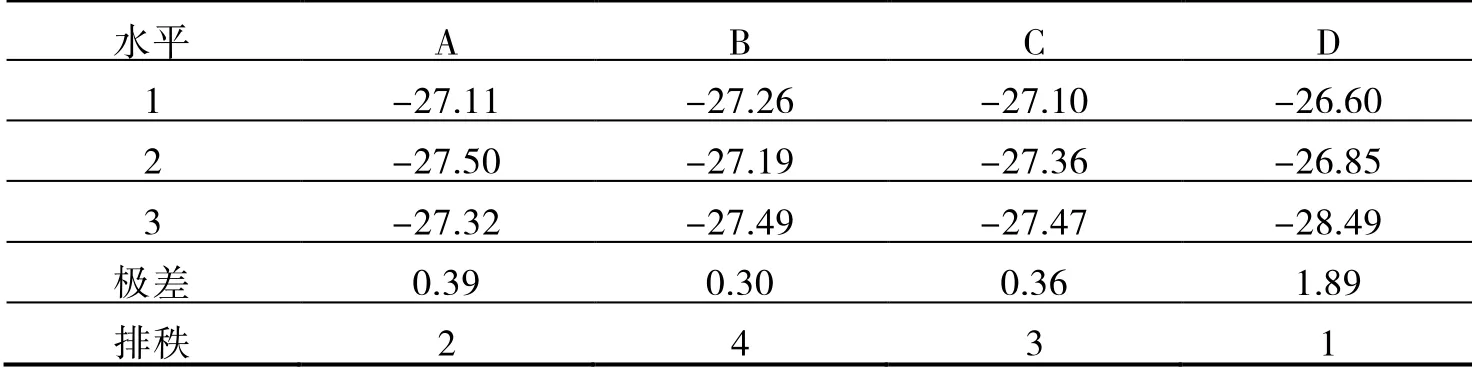
表5 最大變薄率（%）信噪比響應

（2）依據優化目標對零件表面最大增厚率的要求是取極小值，分析試驗因素對最大增厚率的影響程度，通過信噪比響應表6 中的極差排秩可以快速確認因素影響從大到小依次是D、B、C、A。依然是壓邊力的影響最大，其次是模具間隙及摩擦系數。

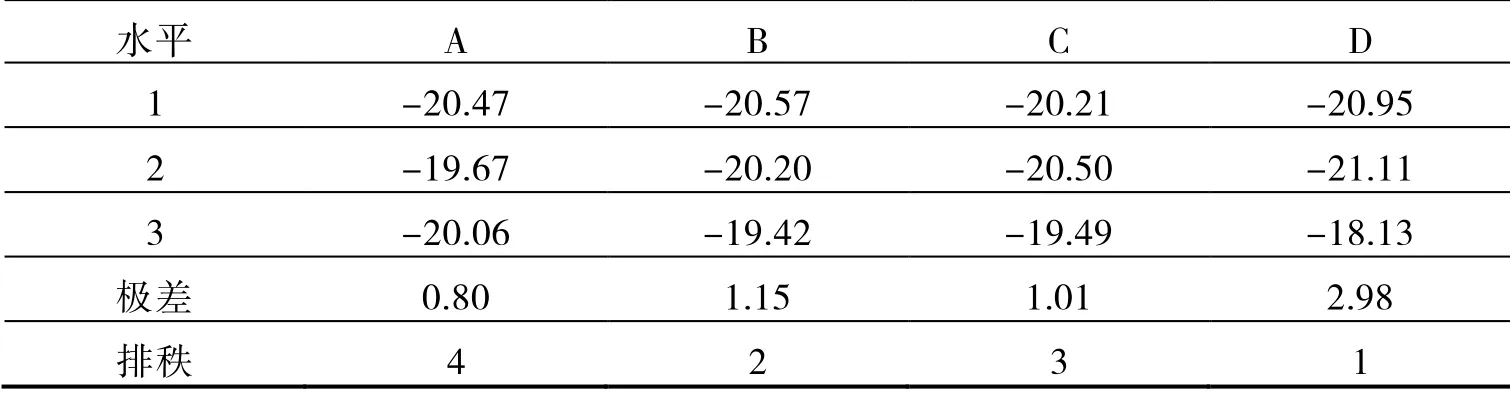
表6 最大增厚率（%）信噪比響應

（3）分析試驗因素對綜合信噪比的影響程度，通過信噪比響應表7 中的極差排秩可以快速確認因素影響從大到小依次是D、B、C、A。即壓邊力的影響程度最大，是最重要因素，其次是模具間隙及摩擦系數。

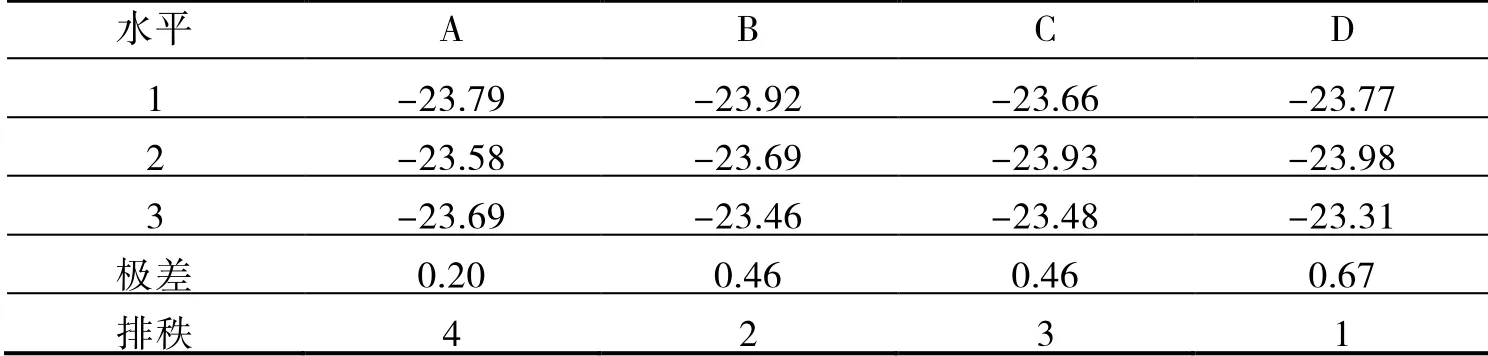
表7 綜合作用下的信噪比響應

3 實物驗證

根據上文田口試驗獲取的最優參數組合，設置現場設備工藝參數，完成實物沖壓試驗，切邊完成后的翼子板零件如圖4 所示。檢查零件外觀，沒有發現明顯的缺陷。為了進一步了解實物零件與仿真模型的成形一致程度，在實物零件與仿真模型表面相同位置標記7 個測量點，通過實際測量獲得實物厚度與實物變薄率，對比結果如表8 所示。

圖4 翼子板鈑金零件

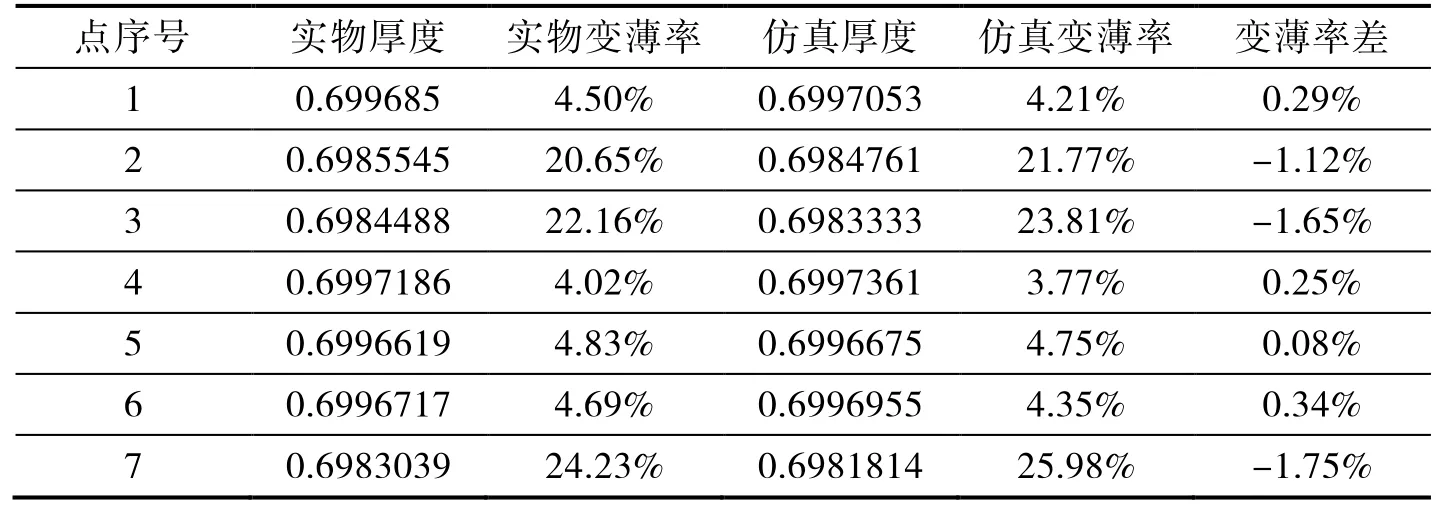
表8 測量點對比

通過對比發現，實物零件變薄率與仿真模型變薄率的最大差值是1.75%，根據目前對塑性加工問題進行仿真的水平，差值在10%以內都被認為是可以接受的合理結果[2]。因此可以判斷，最優參數組合下的仿真模型是合理的，兩者具有較高的一致性，如圖5 所示。

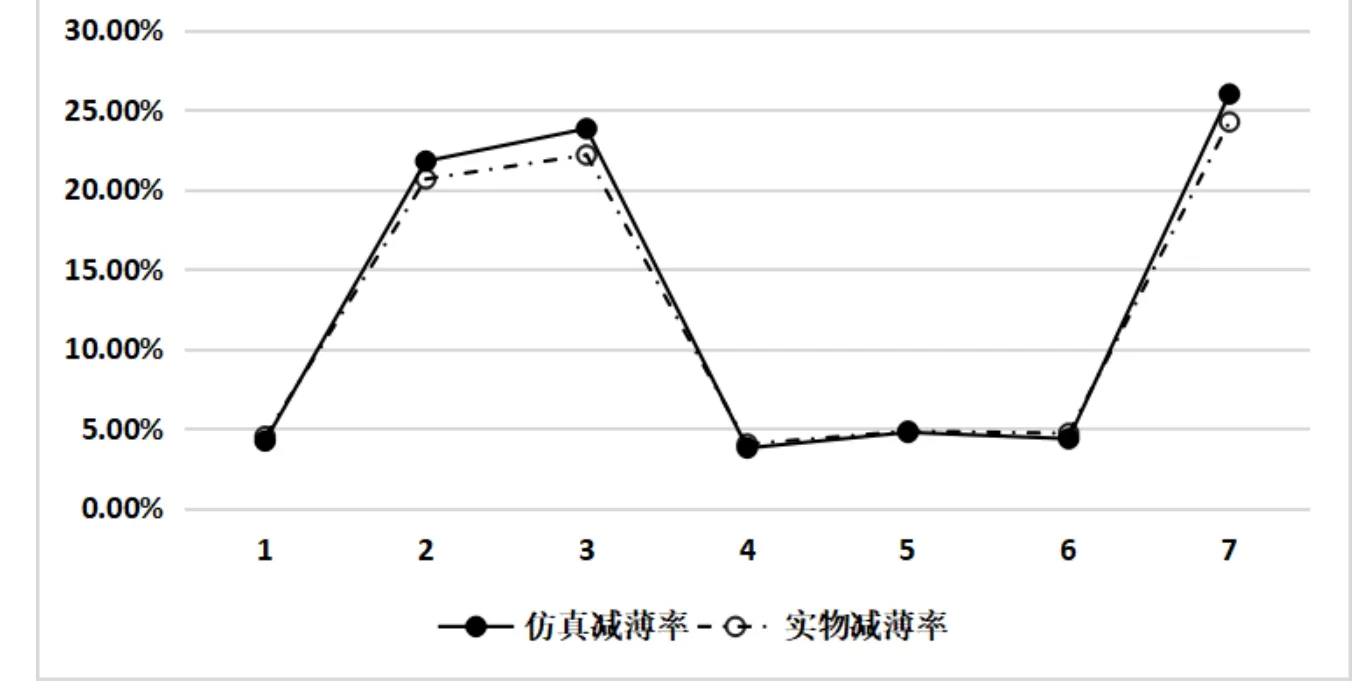
圖5 變薄率對比

4 結論

本文基于工程實際將田口方法運用于汽車翼子板沖壓成形領域，設計了田口的L9(34)正交陣列開展有限元仿真試驗。依據優化目標及約束目標，尋找綜合信噪比最大值，確定最佳工藝參數組合，再使用這組參數進行實物沖壓驗證，并作對比分析，證明了最優參數組合下的仿真模型是合理的。