Jordan標準形的計算與矩陣相似的判定

尹小艷， 楊丹丹， 潘銘櫻

(西安電子科技大學 >數學與統計學院，西安710071)

1 引 言

Jordan標準形理論闡述了一個n階復矩陣在相似意義下最簡單最本質的形式，是線性代數中處理特征值相關問題的常用和重要工具，但線性代數對Jordan標準形的計算并沒有給出好的辦法.本文借助特征值的代數重數和幾何重數， 對三階、四階復矩陣及某些特殊的高階矩陣，給出計算其Jordan標準形的一種簡單有效的方法， 并進一步探討矩陣相似的判定問題，對3階、4階矩陣，分別給出切實可行且易于操作的判定相似的充要條件.這是高等代數、線性代數教學中的一個重點和難點，也是近年來研究生入學考試命題的一個熱點問題[1-4].

2 特征值的代數重數和幾何重數

眾所周知，數λ是n階方陣A的特征值當且僅當λ是其特征多項式|λE-A|的根，非零向量x是A的屬于特征值λ的特征向量當且僅當x是齊次線性方程組(λE-A)x=0的非零解.

定義1對n階方陣A的任意特征值λ，若λ是|λE-A|的m重根，就稱特征值λ是A的m重特征值，也稱λ的代數重數是m，記作mλ=m.特別地，若m=1，稱λ是A的單特征值.

記Vλ={x|Ax=λx}為特征值λ的特征子空間，稱Vλ的維數為特征值λ的幾何重數，記作nλ=dimVλ.根據特征向量的計算方法易知nλ=n-r(λE-A).

3 Jordan標準形理論

Jordan標準形每個n階復方陣A一定與一個Jordan形矩陣J=diag(J1，J2，…，Js)相似，即

?T:可逆，s.t.T-1AT=J=diag(J1，…，Js)，

且這個Jordan形矩陣J除了其中Jordan塊的排列順序外由A唯一確定，稱為A的Jordan標準形，其中第i個Jordan塊為

這里所有Jordan塊的主對角線上元素的集合即為矩陣A的所有特征值(重根按重數算)，可逆矩陣T的各個列向量分別為對應的廣義特征向量.

特別地，當每個Jordan塊都是1階時，Jordan標準形就變成了對角形.

關于矩陣的Jordan標準形，有以下重要結論:

命題1對特征值λi，Jordan標準形J中，以λi為主對角元的Jordan塊的塊數等于λi的幾何重數nλi，而所有這樣的Jordan塊的階數之和等于特征值λi的代數重數mλi.

證由Jordan標準形定理

?T：可逆，s.t.T-1AT=J=diag(J1，…，Js)，

從而A與J特征值相同，而J為下三角形，故其特征值即為所有主對角元素，從而以λi為主對角元的Jordan塊的階數之和必為特征值λi出現的次數，也就是它的代數重數mλi.

關于幾何重數，不妨設J中以λi為主對角元的Jordan塊有2個，即

T-1AT=J=diag(J1，J2，J3，…，Js)，

λiE-A=T(λiE-J)T-1=Tdiag(λiE-J1，λiE-J2，λiE-J3，…，λiE-Js)T-1，

知

且λiE-Jk(k=3，…，s)均為滿秩下三角形，可知λi的幾何重數nλi=n-r(λiE-A)=n-r(λiE-J)=n-(n-2)=2=J中以λi為主對角元的Jordan塊的塊數.若J中以λi為主對角元的Jordan塊有p個，同理可證結論成立.

推論1對n階復方陣A的任意特征值λi，代數重數大于等于其幾何重數，即mλi≥nλi.

顯然，對A的單特征值λ，必有mλ=nλ=1.

Jordan標準形理論表明，任意一個n階復矩陣經過相似變換最簡單可以變成由Jordan塊構成的塊對角形.因此是線性代數和高等代數中處理特征值相關問題的常用工具，比如特征值譜映射定理的證明，比如矩陣函數的計算等.關于Jordan標準形的計算，高等代數[1]中用一整章的篇幅，通過引入λ-矩陣及行列式因子、不變因子、初等因子等概念給出.而利用命題1，對三階、四階矩陣及某些特殊的高階矩陣，可以完全避開λ-矩陣，簡單地計算出Jordan標準形，以下分別分析:

(i) 設A為3階復方陣:

情形1若A有3個互異特征值λ1，λ2，λ3，即mλi=nλi=1，i=1，2，3，則A必可相似對角化，其Jordan標準形必為J=diag(λ1，λ2，λ3).

情形2若A有2個互異特征值λ1(二重)，λ2，即mλ1=2；mλ2=1，此時

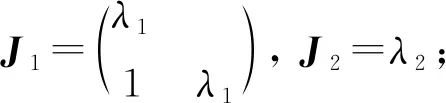
當nλ1=2，A的Jordan塊確定:J1=J2=λ1，J3=λ2.

情形3若A只有1個互異特征值λ1(三重)，即代數重數mλ1=3，于是

當nλ1=3，A的Jordan塊確定:J1=J2=J3=λ1.

(ii) 設A為4階復方陣:

情形1若A有4個互異特征值λ1，λ2，λ3，λ4，則必有mλi=nλi=1，i=1，2，3，4.于是A可相似對角化，其Jordan標準形為J=diag(λ1，λ2，λ3，λ4).

情形2若A有3個互異特征值，則必有且僅有一個特征值為二重特征值，其余均為單特征值.不妨設A的特征值為λ1(二重)，λ2，λ3，則

當nλ1=2時，A的Jordan塊為J1=J2=λ1，J3=λ2，J4=λ3.

情形3若A有2個互異特征值λ1(二重)，λ2(二重)，即mλ1=2；mλ2=2，nλ1=1或nλ1=2，nλ2=1或nλ2=2，從而

當nλ1=nλ2=2時，A的Jordan塊為:J1=J2=λ1，J3=J4=λ2.

情形4若A有2個互異特征值λ1，λ2(三重)，此時

當nλ2=3時，A的Jordan塊為:J1=λ1，J2=J3=J4=λ2.

情形5若A只有1個互異特征值λ1(四重)，即mλ1=4，于是

當nλ1=2 ，此時A有兩個Jordan塊J1，J2，且

當nλ1=4，A的Jordan塊確定:J1=J2=J3=J4=λ1.

解先求矩陣A的特征值得λ1=2，λ2=-2(二重).

對二重特征值-2，幾何重數為nλ2=3-r(λ2E-A)=3-2=1，

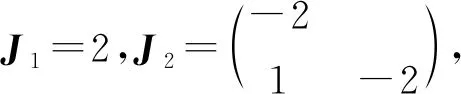
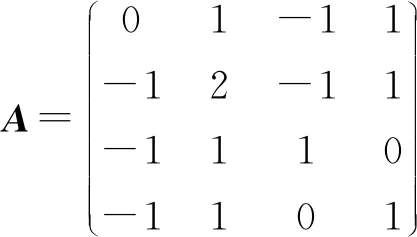
解先求矩陣A的特征值:|λE-A|=-(λ-1)4=0得λ1=1(四重).

事實上， 除了三階、四階矩陣，對某些高階矩陣A，根據命題1，只要A的特征值及其代數重數和幾何重數的值能使我們較為容易地確定出A的所有Jordan塊，就可以確定其Jordan標準形.

解顯然A的特征值為λ1=a1(n重)，且其幾何重數為nλ1=n-r(λ1E-A)=n-(n-1)=1，因此A的Jordan塊只有一個，即為A的Jordan標準形:

解不難看出

4 三/四階矩陣相似的判定

數字矩陣相似關系的判定是高等代數中的一個難點， 通過引入λ-矩陣，有如下結論:

兩個n階復數字矩陣A與B相似

?A與B有相同的初等因子組/不變因子組/各級行列式因子

?A與B的特征矩陣等價.

與Jordan標準形的計算類似，對三階、四階復矩陣及一些特殊的高階復矩陣，利用命題1，可以完全避開λ矩陣及其相關概念，僅通過計算特征值及其代數和幾何重數來判斷相似性.事實上，由相似關系的對稱性和傳遞性，不難得到：

命題2兩個n階復數字矩陣A與B相似

? 他們有相同的Jordan標準形

? 他們有相同的Jordan塊.

根據命題1、2，對3階方陣，其Jordan標準形由其特征值及每個特征值的代數及幾何重數唯一確定.于是若兩個3階復方陣有相同的特征值且每個特征值的代數重數和幾何重數對應相等，則他們的Jordan塊必定相同，從而必相似.

命題33階復方陣A，B相似當且僅當它們有相同的特征值且每個特征值的代數重數和幾何重數對應相等.

深刻理解命題3，可以使我們非常容易地判斷3階復方陣的相似問題，甚至有時僅通過觀察就可以得到正確結論，簡潔明了.比如在2018年全國碩士研究生招生數學科考試(數一、二、三)中有如下題目：

顯然題目所給矩陣為由一個3階Jordan塊構成的Jordan標準形矩陣，由命題1，特征值為λ=1的代數重數mλ=1=3，nλ=1=1，從而與之相似的矩陣應該滿足r(1·E-A)=3-nλ=1=2，在上述4個選項中，顯然只有選項(A)滿足條件，故選(A).

類似地，對4階方陣，由前面分析知，若兩個4階復方陣A，B有相同的特征值且每個特征值的代數重數和幾何重數對應相等，僅當出現mλ1=4，nλ1=2時，需判斷關系式(λ1E-A)2=(λ1E-B)2是否相等，其余情況均可得出A，B的Jordan塊相同，從而相似.

命題4對4階復方陣A，B:

(i) 若A，B有相同的4重特征值λ1，且其幾何重數均為2，則

A，B相似 ? (λ1E-A)2=(λ1E-B)2；

(ii)其余情況下，均有

A，B相似 ?A，B特征值相同且每個特征值的代數重數和幾何重數分別對應相等.

由命題1、2，一般地，對n階復方陣A，B， 有

命題5兩個n階復數字矩陣A與B相似，則它們有相同的特征值，且每個特征值的代數重數和幾何重數分別對應相等.

命題5的條件必要非充分，經常可以用來判定n階復方陣A，B不相似.

解顯然A，B的特征值均為λ1=1(n重)，但對矩陣A，其幾何重數為nλ1(A)=1，而對矩陣B，其幾何重數為nλ1(B)=n-r(λ1E-B)=n-(n-2)=2，因此A，B必不相似.

5 結 論

本文借助于特征值的代數重數和幾何重數的概念， 討論了Jordan標準形的計算及數字矩陣相似關系的判定問題.分別對三階、四階復矩陣， 給出一種計算其Jordan標準形的簡單有效的新方法； 同時，對3階、4階矩陣，分別給出了相似判定的充要條件， 并得到任意n階復方陣相似的一個必要條件；多個數值例子驗證了所得結果的有效性.本文工作為Jordan標準形的計算及矩陣相似的判定進行了有益探索，加深了同學們對相關理論、技能的理解和掌握.

致謝參考文獻4對本文工作有很大啟發， 審稿人的寶貴建議使本文得到進一步完善， 在此一并表示衷心感謝!