一個三角形幾何不等式的推廣
單佳驪, 樓紅衛
(1.復旦大學 >附屬中學,上海200433; 2.復旦大學 >數學科學學院,上海200433)
1 引 言
在幾何不等式研究中,三角形幾何不等式的研究占有重要地位.一些三角形幾何不等式非常簡潔優美,證明思路通常利用余弦定理等三角函數性質去證,解法簡單快捷.如下是第3屆國際數學奧林匹克IMO競賽題中一個三角形幾何不等式及其解法.

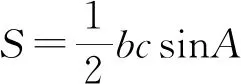
又由Cauchy不等式知b2+c2≥2bc,再結合sin(A+π/6)≤1,得到
且等式成立當且僅當a=b=c(即當且僅當b=c且A=π/3).證畢.
上述解法巧妙地運用了三角形中各邊長和面積與三角函數之間的關系,再結合Cauchy不等式而快速得到原命題.受命題1啟發,有兩個問題值得我們思考和研究:
(i) 能否將命題1中的三角形幾何不等式推廣為更一般的三角形幾何不等式?
(ii) 能否將命題1中的三角形幾何不等式推廣為多邊形幾何不等式?
有很多文獻研究了三角形幾何等式和不等式乃至多邊形幾何等式與不等式,例如文獻 [1-2]研究了三角形幾何等式、不等式及其推廣,文獻[3-4]研究了圓外切和圓內接多邊形幾何不等式.本文將利用凸函數的Jensen不等式[5],將幾何問題轉化為代數問題,獲得比命題1更具一般性的三角形幾何不等式(見第2節推廣1)和圓外切多邊形幾何不等式(見第二節推廣2).
2 主要結論及其證明
首先,將命題1的三角形幾何不等式推廣到更一般的三角形幾何不等式.
推廣1設a,b,c為某個三角形的各邊長,S為其面積.則對任意大于1的實數α,有
aα+bα+cα≥2α31-α/4Sα/2,
其中等式成立當且僅當a=b=c.
其次,將命題1由三角形情形推廣到更一般的圓外切多邊形情形.
推廣2對于n≥3, 設a1,a2,…,an為某個圓外切多邊形的各邊長,S為其面積.則對任意大于1的實數α,有
其中等式成立當且僅當a1=a2=…=an.
接下來,結合Jensen不等式,將把推廣1和2這兩個幾何問題轉化成代數問題,這將大大簡化證明過程.先給出二個重要引理:
引理1令x1,x2,…,xn為正數,n≥1.則對任意不小于1的正數α,有
證令f(x)=xα,x∈(0,+∞),則f″(x)=α(α-1)xα-2>0,x∈(0,+∞).因此f是(0,+∞)上的凸函數.由凸函數的Jensen不等式知:當x1,x2,…,xn>0時,有
即
其中等式成立當且僅當x1=x2=…=xn.證畢.
引理2設n≥1,實數x1,x2,…,xn∈(0,π/2).則
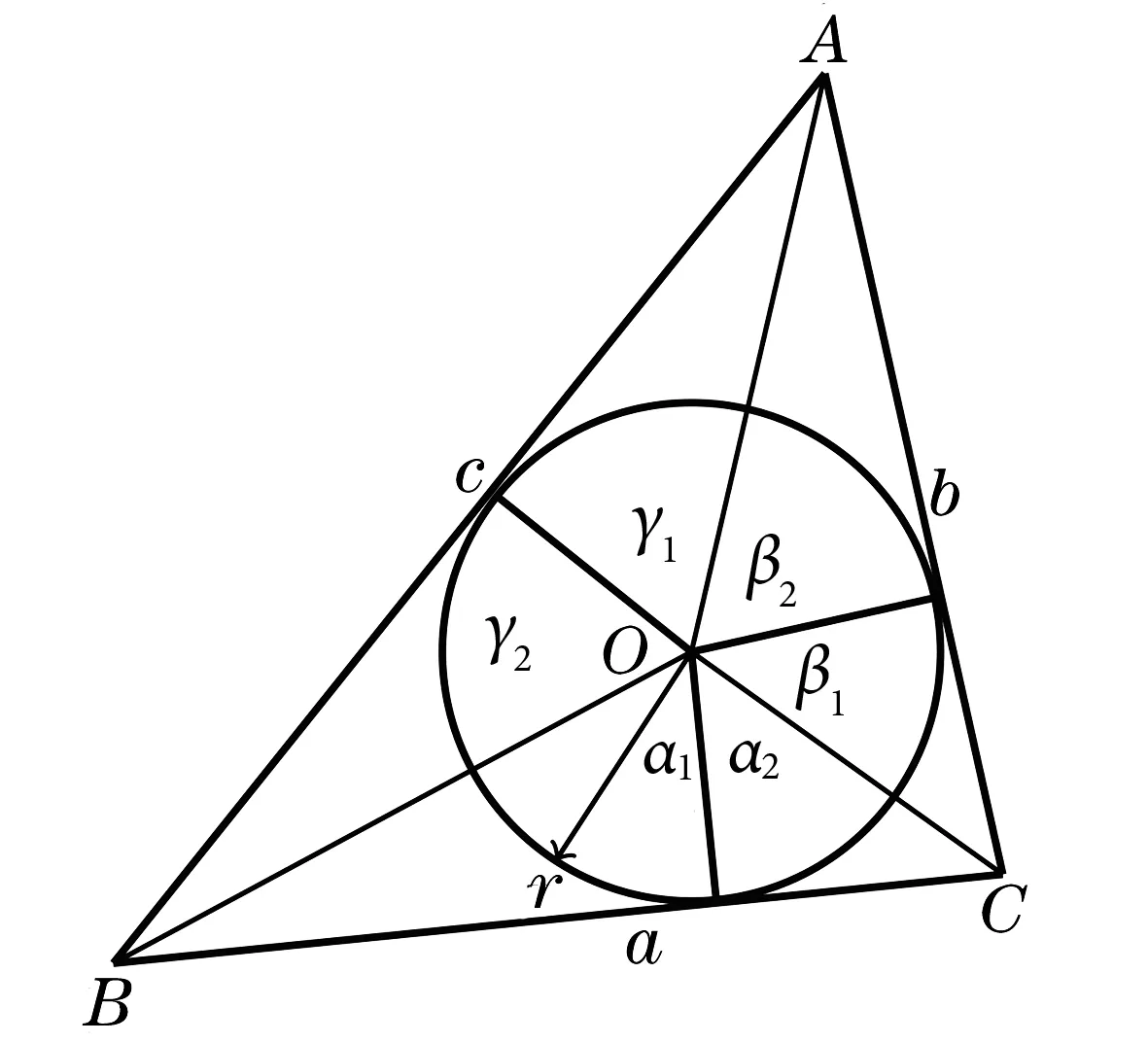
圖1

其中等式成立當且僅當x1=x2=…=xn.
證取f(x)=tanx,其中x∈(0,π/2).則f″(x)=2sinx(cosx)-3>0,x∈(0,π/2).因此f是(0,π/2)中的凸函數.由凸函數的Jensen不等式知
選取定級因素因子體系和確定其權重是耕地定級關鍵的一步。考慮到耕地的自然、社會、經濟與區位屬性,需要選取的評價因素因子較多,計算量較大,利用GIS對空間信息強大的采集、存儲、分析、管理能力是耕地定級及對成果進行科學管理的有效途徑[12-16]。
即
其中等式成立當且僅當x1=x2=…=xn.證畢.
下面給出推廣1和2的證明.
推廣1 證設ΔABC的內切圓圓心為O,半徑為r(見圖1),則
從而有
故
a+b+c=r[(tanα1+tanα2)+(tanβ1+tanβ2)+(tanγ1+tanγ2)],
由于α1,α2,β1,β2,γ1,γ2∈(0,π/2),應用引理2得
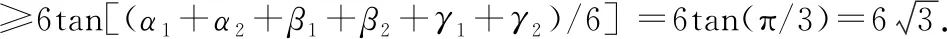
所以
(a+b+c)2=r2(tanα1+tanα2+tanβ1+tanβ2+tanγ1+tanγ2)2
=2S(tanα1+tanα2+tanβ1+tanβ2+tanγ1+tanγ2)
即
其中等號成立當且僅當α1=α2=β1=β2=γ1=γ2=π/3,即a=b=c.又由引理1知
(aα+bα+cα)/3≥3-α(a+b+c)α,
故
其中等式成立當且僅當a=b=c.證畢.
推廣2 證設正整數n≥3,n邊形的頂點依次為A1,A2,…,An,邊長依次為a1,a2,…,an,內切圓圓心為O,半徑為r,各邊所對的兩個內頂角分別為β2i-1,β2i(1≤i≤n).則類似推廣1的證明,有
由引理2知
所以有
即
a1+a2+…+an≥(4nStan(π/n))1/2,
且等號成立當且僅當β1=β2=…=β2n=tan(π/n),即a1=a2=…=an.
再由引理1知,對任意大于1的實數α,
從而我們有
其中等式成立當且僅當a1=a2=…=an.證畢.
3 結 語
本文從一個三角形幾何不等式出發,利用凸函數的Jensen不等式,把幾何不等式問題轉化到代數不等式的證明,證明思路簡潔快捷,并獲得了更一般的三角形幾何不等式及圓外切多邊形幾何不等式.類似問題對于提升高中階段的學生學習數學的興趣和進行初步的研究有很大幫助.
致謝感謝復旦大學“步青”高中生學術見習計劃,感謝參考文獻給予我們的啟發.

