數學專業《概率論》課程交叉融合的探索與實踐
楊廣宇, 趙建彬
(1.鄭州大學 >數學與統計學院,鄭州450001;2.河南省大數據研究院,鄭州450001)
1 引 言
隨機的想法已經滲透到科學的各個角落,在連續幾屆 Fields 獎授予概率學者(2006 Wendelin Werner,2010 Stanislav Smirnov,2014 Martin Hairer)之后,2019 年Wolf 獎授予了兩位概率大師Gregory F. Lawler,Jean-Fran?ois Le Gall,2019年邵逸夫獎授予了概率大師Michel Talagrand. 這些都表明:概率論已正式進入主流數學領域.在此背景下,作為數學專業基礎課的《概率論》課程該如何開展呢?筆者一直堅信,教學不僅是傳授知識,更重要的是啟智,為學生多打開幾扇窗;此外,數學是一個整體,概率與現實世界關系緊密,因而是可以讓學生結合所學內容做一些相關性研究課題的,譬如Berkerley大學統計系David Aldous的創新性課程Probability and Real World就是結合現實問題以分組課題研究形式來開展的.劉柏森[1]對概率統計研究性教學改革做了一些有益的討論;周玲[2]結合抽象思維能力的培養,給出了概率論研究性教學的一點思考;秦旭等人[3]探討了概率論與數理統計教學中課程小論文寫作對學生創新能力培養的作用.如上文獻大多是在大學公共課背景下進行的教學研究探索,筆者結合數學專業實際情況,在教學中針對學科融合式的研究性教學做了一些有益的嘗試,主要圍繞概率論中的基本結果,著重于隨機的想法與各學科,譬如分析、代數、物理等的交互滲透,特別強調了概率方法的“潤滑劑”效應.
2 交叉融合的教學探索與實踐
結合我院數學與應用數學專業培養方案,緊扣《概率論》課程教學大綱,針對某些知識點,將學科融合式研究性教學加入了教學設計,開展了一些專題性教學探索與實踐.
2.1 Jordan公式應用之自然數互素問題
引入概率公理化定義之后,通常會討論概率的一些基本性質,譬如加法公式等,而如下的Jordan公式則是加法公式的自然推廣.
定理1(Jordan 公式,[4]) 設(Ω,I,P)是完備概率空間,An∈I,n≥1,則
(1)


定義

則由Jordan 公式可得
(2)
注意到
因而可得
其中無窮乘積中的q取遍所有素數.又由Euler乘積公式
(3)

注 關于兩個自然數互素的問題有很多相關討論,譬如文獻[6].可以進一步地問:任取r個自然數,它們恰好互素的可能性是多少?它們恰好兩兩互素的可能性又是多少?并且這些問題能否推廣到有限域上多項式環呢?譬如任意取兩個多項式,它們恰好互素的可能性有多大呢?這些都牽涉到概率思想的應用,且沒有超出本科生的學習范圍,因而可作為本科生研究課題,讓學生進行分組探索,增加趣味性之余,也鍛煉了學生的科研能力.
2.2 獨立性探討之Euler乘積公式與素數無窮多之概率證明
為理解獨立性,課程中試著構造合式的概率空間,用概率的想法來討論Euler乘積公式及素數有多少個的問題.
考慮如下的概率模型:
其中ζ(s)為如前所定義的Riemann zeta函數,則(Ω,I,P)是概率空間.任給正整數m,記Dm=m+,則Dm∈I,并且有
令p1,p2,…,pk為k個不同的素數,有Dp1p2…pk=Dp1∩Dp2∩…∩Dpk,因而

(4)

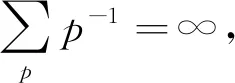
注 獨立性是概率論中最重要的概念之一,隨機思維也有其獨特作用,其與Euler乘積公式及素數的多少沒有任何關系,但是通過適當概率模型的構造,卻能用概率工具給出數論中深刻定理的簡易證明,這不但震撼了我,更震撼了學生,讓其對獨立性、概率思維及數學的統一性有了更深的理解.注意到,Martin Aigner, Gunter M. Ziegler[7]所著《Proofs from THE BOOK》中開篇就是“素數無限的六種證明”,其充分體現了分析、代數、幾何與拓撲,也即數學的統一性!事實上,概率方法在數論中很活躍,也很深刻,Pal Turan, Alfred Renyi, Mark Kac, Paul Erdos等在這方面有開拓性的貢獻,該領域針對本科生也有很多有趣的課題可做,譬如Mark Kac的優美小書[8].
2.3 條件概率之隨機游動與輸光問題
設某粒子在整數格子點上運動,其出發點為0,若時刻n處于位置x,則n+1時刻處于位置x+1的概率為p,處于位置x-1的概率為q=1-p. 用Sn表示粒子時刻n所處的位置,則有S0=0,
P(Sn+1=x+1|Sn=x)=p=1-P(Sn+1=x-1|Sn=x).
稱{Sn,n≥0}為整數格子點上的簡單隨機游動.
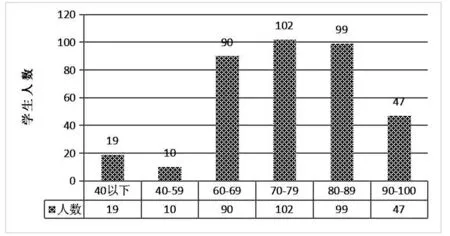
輸光問題是隨機游動理論中的一個經典問題:拋一枚硬幣,P(“正面”)=p,P(“反面”)=q=1-p,甲乙兩人進行如下賭博游戲,獨立拋擲該硬幣,若“正面”出現,則甲贏得一元錢,若“反面”出現,則甲輸掉一元錢;現給定正整數N,設甲初始有0≤x≤N元錢,若甲的錢數達到0或者達到N,則游戲結束,試問游戲以甲輸光結束的概率?注意到,該問題恰好可以用前面的隨機游動模型來描述.記Sn為n局后甲擁有的錢數,ux=P(甲輸光|S0=x),則對任意的整數0 ux=P(甲輸光,S1=x-1|S0=x)+P(甲輸光,S1=x+1|S0=x) =qP(甲輸光|S1=x-1,S0=x)+pP(甲輸光|S1=x+1,S0=x) =qux-1+pux+1. (6) 注意到u0=1,uN=0. 解上述帶邊界的線性方程組可得 (i)p=q=1/2,ux=(N-x)/N; (ii)p≠q,ux=[(q/p)x-(q/p)N]/[1-(q/p)N]. 顯見,若游戲是公平的,則甲初始資本越小,其輸光概率越大,初始資本越大,其輸光概率越小. 注 教學實踐中,可鼓勵并指導學生分小組進行延伸閱讀,如隨機游動的常返與暫留問題、隨機游動與電網理論(離散位勢理論)、自規避隨機游動、高分子聚合物的隨機游動模型、金融領域的隨機游動假設等等;結合R語言或Python的應用,也可對隨機游動、自規避隨機游動的軌道進行模擬研究,進而導出布朗運動. 概率論中的一階矩、二階矩方法非常簡單,但其使用方便、威力巨大.為體現學科交融,課堂上分別從分析和組合兩方面討論了該方法的應用. 定理2(一階矩方法,[9]) 設X是非負隨機變量,則 (i) 對任意t>0,有P(X≥t)≤E(X)/t; (ii) 進一步的,若又有E(X2)<∞,則對任意t>0,有P(|X-EX|≥t)≤Var(X)/t2. 定理3(二階矩方法,[9]) 設X是非負隨機變量且E(X2)<∞,則 (i) 對任意0≤t≤1,有P(X>tE(X))≥(1-t)2[E(X)]2/E(X2); (ii) 特別的,有P(X>0)≥[E(X)]2/E(X2). Weierstrass逼近定理設f∶[0,1]→是連續函數,則對任意ε>0,存在多項式函數p(x)使得也即多項式函數在(C([0,1]),||·||)中稠密. 證該證明屬于Bernstein. 任給0≤x≤1,令Bn~Bin(n,x),定義n次多項式 注意到 其中Aδ={ω∈Ω:|x-Bn/n|>δ}. 由于f是[0,1]上連續函數,因而可取到最大值并且一直連續.從而可選適當的δ使得 另一方面,應用Chebyshev不等式可得 P(Aδ)=P(|x-Bn/n|>δ|)≤x(1-x)/(nδ2)≤1/(4nδ2), 可選充分大的n使得任意的0≤x≤1,都有 注意到,{2i,0≤i≤log2(n)}是具有不同和的,因而f(n)≥log2(n)+1. Paul Erdos 猜想:存在常數C使得f(n)≤log2(n)+C. 可“無中生有”,用概率方法給出f(n)的一個上界估計. P(|X-E(X)|>t)≤t-2Var(X)=λ-2. 因而 由注意到Var(X)≤kn2/4,有 由λ>1及其任意性可知 從而可得 k≤log2(n)+2-1log2(log2(n))+O(1). 也即得到了f(n)的一個上界估計. 注 Weierstrass逼近定理是分析中的經典結果,將概率思維應用過來,證明顯得清晰又簡潔,是概率與分析交融的典型代表;不同和是組合數學中的一個有趣問題,這里雖沒有隨機的影子,但通過隨機想法的引入,應用簡單的概率方法卻給出了該問題的一個上界估計,其雖距離Paul Erdos的猜想還有一段距離,但讓學生體驗到概率威力的同時也有了研究課題:能否進一步精確上界估計呢?事實上,概率方法與組合數學相互交融,博大精深,妙趣橫生,可參見專著 [9].一階矩、二階矩方法除上面應用之外,在其它領域,譬如概率數論、圖論、隨機算法、滲流等等,也有很廣泛的應用.特別的,滲流是統計物理中的一個重要領域,其問題敘述簡單易懂,但解決極其困難,在此領域已產生多位Fields獎得主,但是在本科概率論教學中卻可以應用一階矩、二階矩方法給出樹上滲流概率的一個簡單估計,這不但可以拓展學生的視野,展示隨機想法的威力,更能激發學生學習概率的興趣. 在概率論課程中有意識地引入交叉融合式研究性教學設計,主要萌發于本人對數學統一性的看法及初心——播下隨機的“種子”.至今,共實踐有四屆約367名學生.在課程開始、期中、期末及學生考取研究生后都有一定的跟蹤反饋并做了一些調查,應該說部分達到了目標——增加了學生對隨機的興趣,播下了幾粒隨機的種子.筆者給出了關于調查和反饋的簡單統計分析圖,見圖1、圖2. 圖1 興趣變化趨勢圖 圖2 概率論期末成績 從圖中可以看出,隨著課程的展開,充分調動了大多數同學的積極性與興趣,特別是有些同學有持續的濃厚興趣;課下與學生溝通及學生評教系統反饋也證實了這一點;課程難度有所增大,對學生的努力程度要求比較高,少部分同學選擇了放棄,部分同學嘗試進行了課題研究,并撰寫了研究報告,這在期末成績上也有體現. 以上是筆者在我院數學與應用數學專業本科《概率論》課程教學過程中關于學科融合式研究性教學的一點探索和實踐,期間也出現了一些問題,譬如在教學改革中怎樣掌控課程的廣度與深度,平衡教師、學生關系,選取恰當的學科材料,因材施教等等,希望本文可以起到拋磚引玉的作用.事實上,上述只是冰山一角,諸如Erdos-Renyi隨機圖的相變現象、期望與朋友圈、優惠券收集、矩問題、Borel-Cantelli引理之圓周覆蓋問題等等,契合本科生的研究課題大有可為.特別的,李賢平、方毅[10]與David Aldous的網上課程都是非常好的資源,有很多生動活潑的本科生可操作的課題,所謂教學相長可能就來源于斯.或許部分教師認為本人的這些探索和實踐過于數學化、理想化,失去了趣味性,概率應該更生動活潑.其實,教師可借用多種手段向學生展示概率的思維特點,讓學生自己去體味概率的魅力,在數學統一性上去欣賞她的美,從而不斷地提高其數學素養.如果確覺無味,可嘗試把R語言及Python引入進來,讓學生做一些隨機模擬,譬如重要分布、大數定律及中心極限定理的可視化,蒲豐投針的進一步研究與蒙特卡洛算法,Bayes公式再認知,隨機游動軌道實現等等.作為師者,對“概率”懷癡愛之心,不斷去理解“她”,盡可能把“概率思維”的魅力通過各種途徑展現出來,進而激發學生的探究之心,最終達到師者傳道啟智之初心. 致謝作者衷心感謝審稿人,其有益建議使得本文得到了很大的改進!2.4 一階矩、二階矩方法之分析與組合






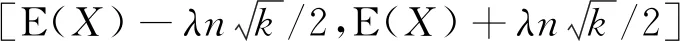
3 教學效果

4 結 論

