空間密集目標的群分割算法研究
韓蕾蕾,周 璐
(海軍航空大學 研究生大隊, 山東 煙臺 264001)
彈道導彈等空間目標在中段飛行期間,利用地心引力和最初獲得的慣性進行運動,運動特性較為穩(wěn)定[1]。由于地球近地軌道空間氣體密度非常低,空氣阻力幾乎可以忽略不計,中段運動中釋放的各種干擾誘餌,除了與彈頭有較小的相對速度外,其初速度全部來源于彈頭攜帶升空后的慣性,各目標之間軌道速度基本相同。相同的軌道速度,較為接近的空間位置,可以作為空間密集群目標進行研究[2]。誘餌釋放初期,目標數(shù)目以及目標間距會超出傳感器的檢測跟蹤能力范圍,傳感器并不能目標群中的每個目標,且目標空間分布的密集性易造成目標航跡間的關聯(lián)錯誤,這些會引起跟蹤的不穩(wěn)定。為了盡早精確預報空間威脅彈頭,就必須通過穩(wěn)定的跟蹤提高數(shù)據(jù)精度,而且誘餌釋放初期離彈道攔截還有相當長的一段時間和距離,此時并不需要精確跟蹤到彈頭和每個誘餌目標,只需要掌握空間目標群的整體的運動態(tài)勢即可,即可以對群整體進行跟蹤。誘餌與空間彈頭間距隨著時間推移會逐漸增大,因此要對目標群進行自適應群分割,通過對逐步分裂的子群進行群整體跟蹤,來延長穩(wěn)定跟蹤的時間,提高跟蹤精度。
由于空間密集目標分群是在目標跟蹤步驟之前,因此量測集劃分是態(tài)勢估計的關鍵步驟,其分群效果直接影響狀態(tài)估計和濾波算法性能[3-4]。空間目標敵我屬性明確,因此群分割主要按照位置關系對空間上目標進行的集合劃分。目前,空間目標群分割的主要方法就是距離分割法[5-6]以及其改進后的循環(huán)閾值法[7],其都是通過設定距離閾值實現(xiàn)分群,其原理簡單易實現(xiàn),但是空間目標的高密集性容易導致各時刻分割群中成員數(shù)量產生波動,從而使分群結果缺乏穩(wěn)定性。
針對上述問題,本文提出了距離劃分與預測劃分相結合的聯(lián)合劃分法。算法在航跡起始階段,通過設定與傳感器分辨能力相關的距離閾值,實現(xiàn)無預測信息以及預測信息不可靠條件下的有效分群;在航跡維持過程中,將貝葉斯遞推狀態(tài)和形態(tài)進行聯(lián)合[8-10],將落入某群預測形狀波門的所有量測劃分為一個群,求取群量測中心并帶入群更新的迭代計算中。同時在群量測求取過程中利用概率數(shù)據(jù)關聯(lián)[11]的思想代替坐標平均法來獲得更為準確的等效群中心。通過聯(lián)合劃分法分群保證了各階段分群的穩(wěn)定性,提高群質心的精度,可減少后續(xù)關聯(lián)錯誤,提高跟蹤的準確性。
1 問題描述
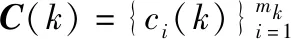
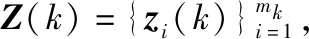
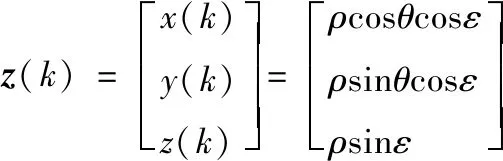
對應k時刻直角坐標系下的量測噪聲協(xié)方差為
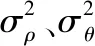
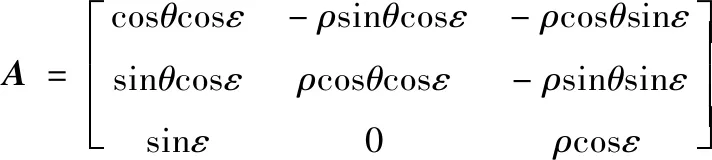
群分割就是對ENU坐標系下的量測集Z(k)及其對應的協(xié)方差集R(k)根據(jù)一定的準則進行劃分。距離劃分法中,通過設定與傳感器分辨率相關的距離閾值即可實現(xiàn)自適應分群。但由于空間目標具有高密集性,即使已經(jīng)分裂開的兩個子群也很容易由于其邊緣某些量測的相近性而被劃分為一個群來進行跟蹤,這樣相近的測量時刻中各目標群會反復分裂與合并,進而使群狀態(tài)估計產生較大的誤差。因此文中考慮只在無預測信息或者預測信息不可靠的航跡初始階段考慮采用距離劃分方法進行群分割,在航跡起始成功后,考慮通過形狀波門對下一時刻的量測進行聚類,其劃分結果與當前時刻的預測群中心以及預測形狀矩陣相關,即使在目標量測比較近時,也能將量測劃分給不同的群中心,從而避免兩個群的合并,得到誤差相對較小的狀態(tài)和形狀估計。
2 距離劃分法
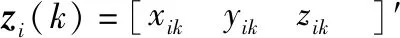
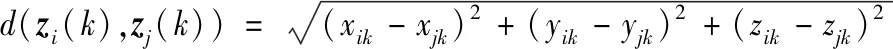
(1)
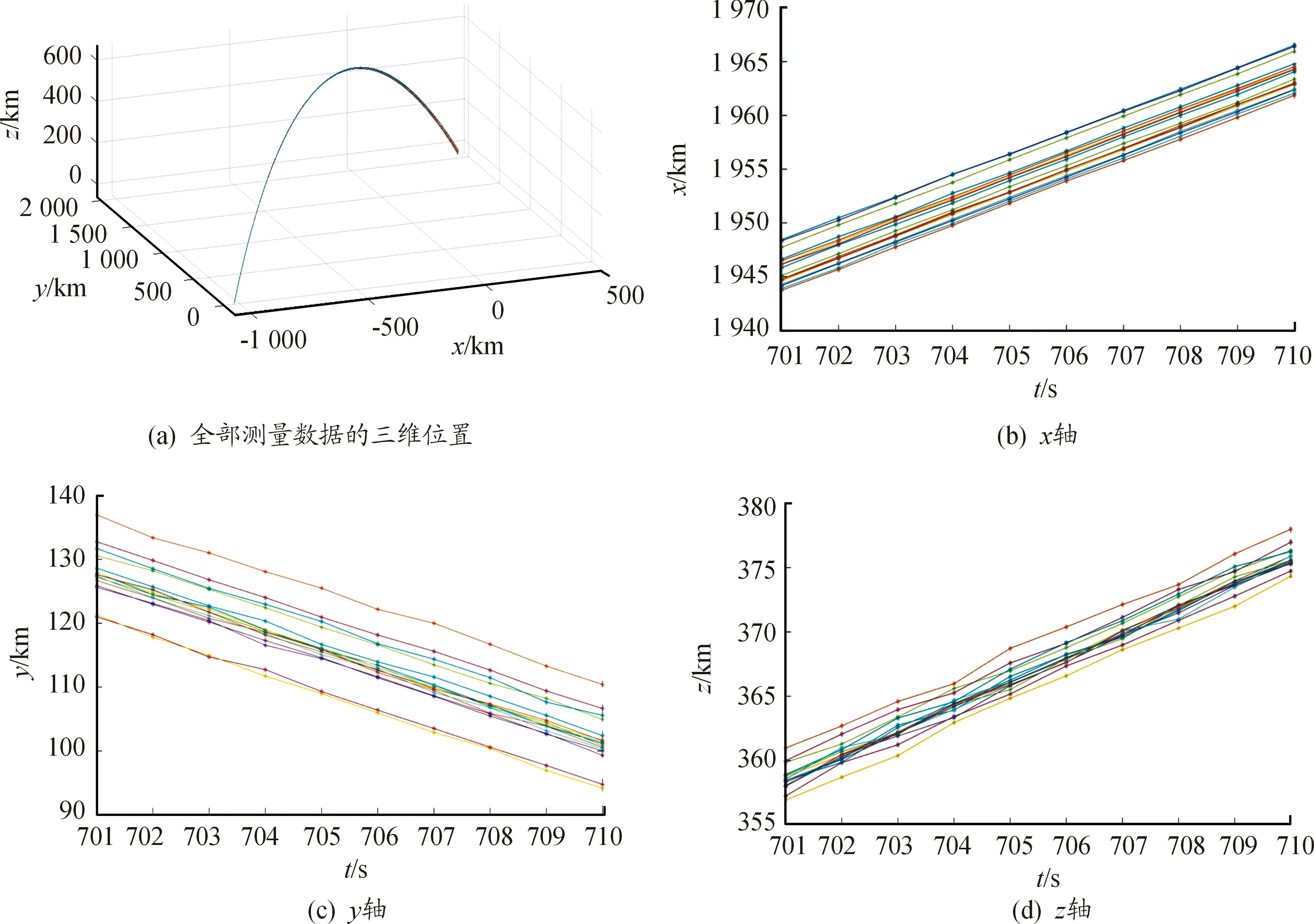
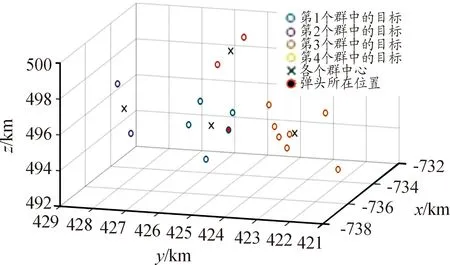
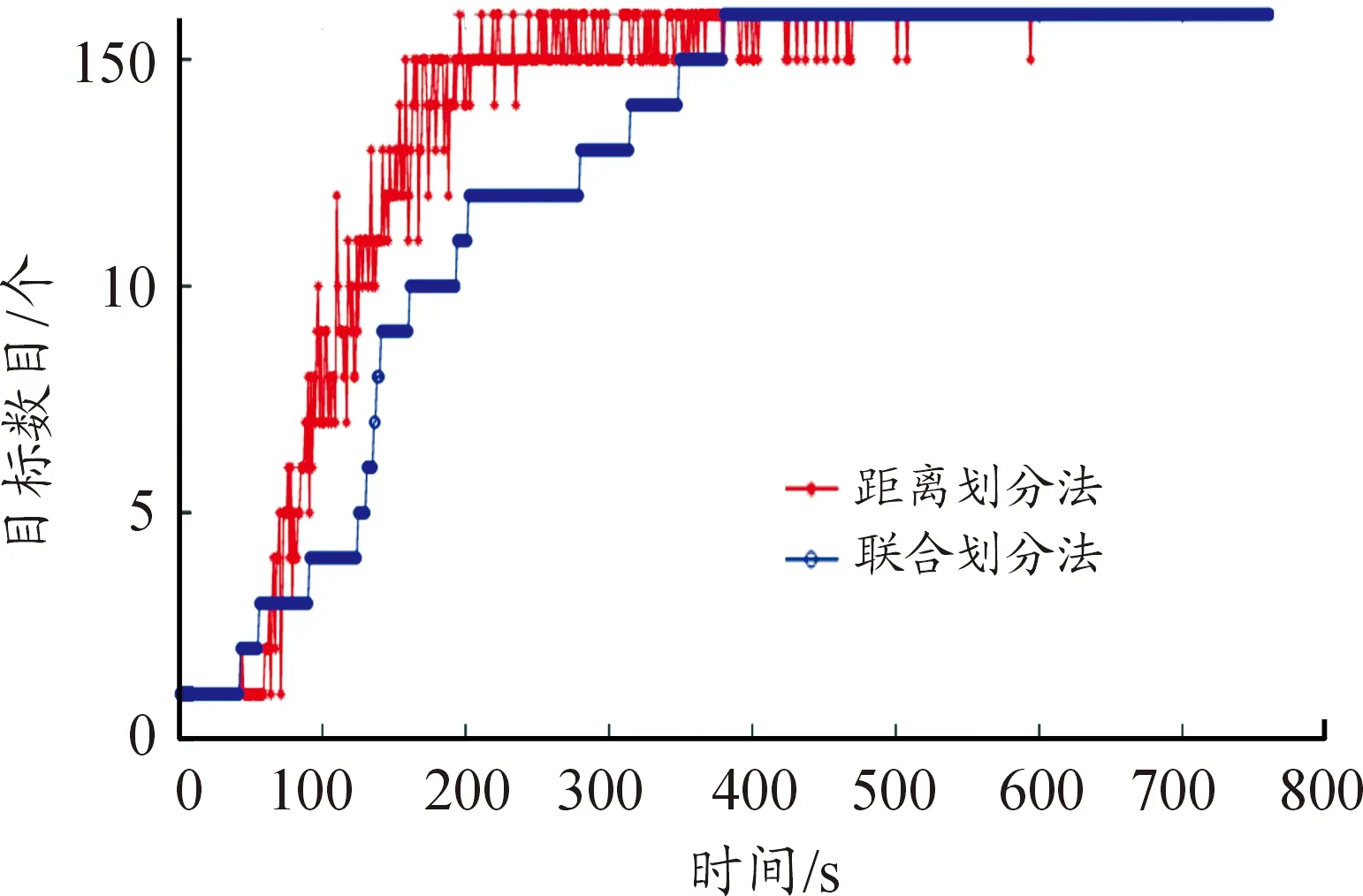
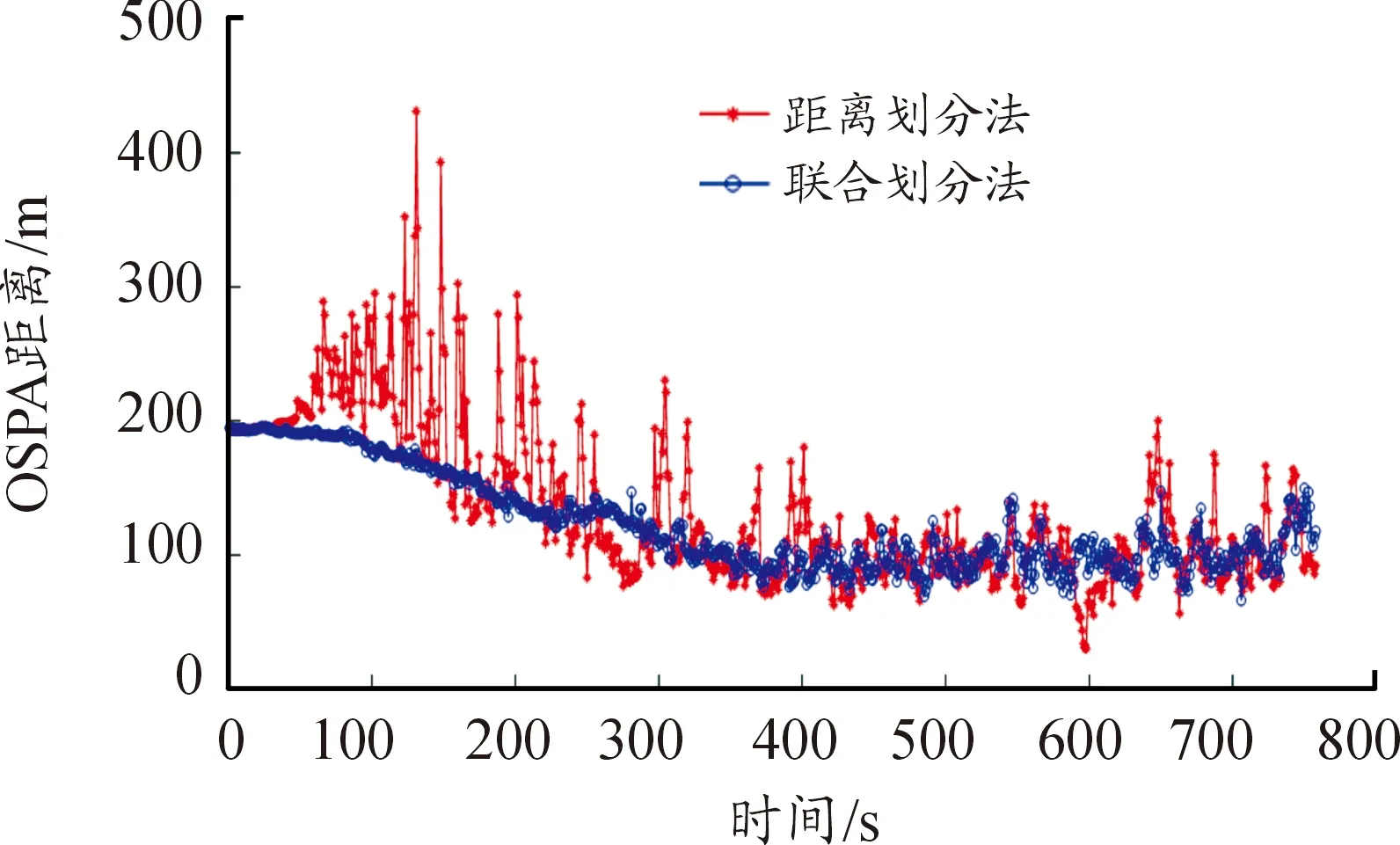
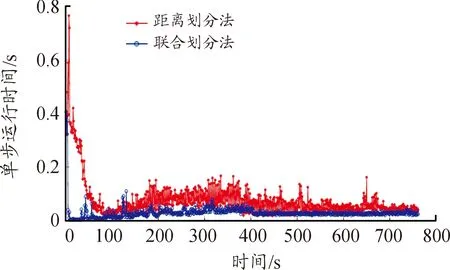
若d(zi(k),zj(k)) 利用式(1)計算Z(k)中任意兩個量測之間的距離并與d0比較,可最終將Z(k)分割成多個不同的群。設Z(k)最終可分為m個群,記為{U1,U2,…,Um},且 定義兩個不同的群Ui和Uj之間的距離為 1≤m≤ni, 1≤n≤nj 當d(Ui,Uj)≥d0,Ui和Uj為分離的兩個群;當d(Ui,Uj) 1≤m≤ni,1≤n≤ni,m≠n (2) (3) 距離劃分法一般任意選取一量測為種子量測劃分波門,將落入波門內的全部量測劃分給該群,歸類完畢后再在剩余量測中選擇另一個種子量測,以此類推進行分類,同時還要判斷兩個群間的距離是否滿足合并條件;循環(huán)邏輯法則是以落入波門內的每一個量測為中心重新建立波門,尋找落入新波門內的量測。兩種算法都具有一定的邏輯復雜性,文中給出了另一種相對簡單的邏輯思路,即將滿足距離閾值條件的量測對全部篩選出,然后統(tǒng)一進行合并劃分,其算法具體實現(xiàn)如下: 1) 求量測間距離。根據(jù)公式求取當前時刻k所有量測間距離并存儲,可得到mk(mk-1)/2個量測間距離。 2) 預分割群。找到所有距離元素的最小值,若該最小值小于距離閾值d0,則把該距離對應的位置坐標及量測編號i,j進行存儲,同時將該最小距離賦值為無窮大,讓其不參與下次最小值的競爭,重復上述步驟,直至最小值大于閾值,至此篩選出所有滿足閾值要求的預分割群u1,u2,…,ul,各個群之間有大量重復元素,后續(xù)步驟主要通過量測編號判斷是否進行群的合并及單目標群的劃分。 3) 進行群的合并。若兩個量測群中有重復元素,則進行合并運算得到一個群,重復步驟,直到所有群之間沒有重復元素為止,至此得到n個群U1,U2,…,Un。 4) 劃分單目標群。在完成上述步驟后,若判斷量測集Z(k) 中還有剩余量測并不屬于劃分的任何一個目標群,則該量測單獨分為一個群,得到單目標群Un + 1,Un + 2,…,Um,至此量測集Z(k)最終分割為m個群,記為{U1,U2,…,Um}。 5) 求取群中心數(shù)據(jù)。根據(jù)式(2)和式(3)進行群中心坐標和對應協(xié)方差的求取。 為更準確描述空間目標運動狀態(tài),考慮用空間動力學方程進行約束,因此某質心運動狀態(tài)的動態(tài)模型可描述為 x(k+1)=F(k)x(k)+D(k)gr(k)+ω(k) 其中狀態(tài)轉移矩陣F(k)=F1(k)?Ιd; ?為克羅內克積運算符號,Ιd∈Rd×d為單位陣。d為空間維數(shù),這里d=3。 式中:α為機動時間常數(shù)的倒數(shù);T為采樣間隔。 gr(k)為當前時刻的重力加速度,D(k)=D1(k)?Ιd,且 ω(k)為ENU直角坐標系下零均值的高斯過程噪聲,且 ω(k)~N(0,Q(k)?Xk) 而 Xk為d×d維對稱正定的隨機矩陣,過程噪聲的協(xié)方差矩陣Q(k)?Xk表明,質心運動狀態(tài)的不確定性取決于目標擴展形態(tài)(包括大小、形狀和朝向),目標的形態(tài)越大,其質心形態(tài)的不確定性也越大。 其中:aM為機動加速度的極大值;pM為機動加速度等于極大值的概率;p0為機動加速度等于0的概率。 針對某群目標,運動狀態(tài)的一步預測為 協(xié)方差的一步預測 P(k+1|k)=F(k)P(k|k)F′(k)+Q(k) 量測值的進一步預測 其中 新息 新息協(xié)方差 S(k+1)=H(k+1)P(k+1|k)H′(k+1)+R(k+1) 增益 K(k+1)=P(k+1|k)H′(k+1)S-1(k+1) 狀態(tài)更新方程 與擴展目標類似,空間群目標的形態(tài)可以用對稱正定的隨機矩陣表征[12-14],設k時刻某群目標的橢球方程為 式中:變量y(k)代表橢球表面上的點;H(k)x(k)為群的質心位置;X(k)為正定矩陣,其特征值為橢球中3個軸的長度,方向為橢球3個軸的方向。 形狀一步預測為 形狀更新為 X(k+1|k+1)=X(k+1|k)+N(k+1)+ 其中 N(k+1)=S-1(k+1)V(k+1)V′(k+1) B(k+1)為形態(tài)觀測矩陣,且 nk+1為落入該群波門的量測個數(shù)。 最初3個時刻的群中心為基于距離劃分得到的群中心,后續(xù)預測過程中群中心是根據(jù)落入波門內的量測獲得的。 形狀預測波門為 新一時刻傳感器探測后,判斷選出落入各群波門內的所有量測,由于各群之間距離依舊比較近,各波門之間有交叉重疊,同一個量測可能落入多個群波門中,因此可借鑒概率數(shù)據(jù)關聯(lián)的思想來求取各等效群中心,其關鍵步驟是得到波門內每一個量測來自預測群中心的后驗概率,可用量測j與群中心t的高斯似然函數(shù)[15]求得: 其中,νjt(k+1)為落入群中心t波門內所有量測與群中心t之間的組合新息;S(k+1)為對應的組合新息協(xié)方差。 為了進一步預防相鄰群間的合并,考慮對接近預測位置的量測做重加權,即對互聯(lián)概率基于距離關系進行二次加權。 群中心t與量測j間概率的二次加權值為 其中,m為k+1時刻落入群中心t候選波門的量測個數(shù);rtj為航跡t與量測j間的歐式距離。 量測j與群中心t互聯(lián)概率為 δjt=βjt*wjt 此時得到的航跡t與所有候選量測間的概率之和并不等于1,需要做歸一化處理,最終量測j與群中心t互聯(lián)概率φjt,其中 對于未關聯(lián)上的群目標數(shù)據(jù),采用距離劃分法進行群分割,并按照3/3邏輯法進行航跡起始判別,即有連續(xù)3個時刻的群等效中心滿足航跡起始判斷條件,即判定該航跡起始成功。對于一個新目標群,設其出現(xiàn)的最初時刻為時刻1,后續(xù)相應為時刻2、3。同時將各時刻中所有的群賦予相應的群編號。 1) 建立1-2可能航跡。求取時刻1和時刻2兩個量測i、j之間的距離,若量測間的距離在初始波門內,則判斷初始關聯(lián)成功形成1-2可能航跡,遍歷所有量測間距離,若存在一組量測滿足波門要求,可能航跡的個數(shù)加1,最終得到m條可能航跡,其航跡的編號是根據(jù)存儲時間的前后自動進行編號的,其中初始波門大小為 其中:KG為波門常數(shù);T為采樣間隔;vi為第i個群目標1時刻的最大可能速度。 在所有關聯(lián)判斷結束時,若第1時刻某個群目標的初始波門內無對應的第2時刻的關聯(lián)數(shù)據(jù),則可認為該群目標第2時刻漏檢,該群目標航跡起始失敗;若還有多余的第2時刻數(shù)據(jù)未關聯(lián)上,則將第2時刻該數(shù)據(jù)作為新出現(xiàn)的群目標第1時刻的數(shù)據(jù),重新賦予相應的群編號,然后和后續(xù)時刻的數(shù)據(jù)進行關聯(lián)判斷。 2) 判斷是否形成1-2-3確認航跡。若1-2可能航跡的個數(shù)m為0,則所有航跡起始失敗,否則對可能航跡進一步判斷能否形成1-2-3確認航跡。針對所有可能航跡,根據(jù)其時刻1,2的測量位置進行直線外推,得到時刻3的預測點,并根據(jù)式(4)求取時刻3所有的預測點與所有的測量點之間的統(tǒng)計距離。將預測點位置、1-2時刻量測點的編號和對應距離作為一個關聯(lián)對存儲在數(shù)組中。 (4) 將所有距離進行排序,選取其中的最小距離,若Dmin≤γ,則其對應的1-2可能航跡與時刻3測量點關聯(lián)成功,確認航跡數(shù)量增加并將其對應的1,2,3量測進行存儲,然后刪除與已關聯(lián)的預測點和時刻1、2量測點相關的所有關聯(lián)對的數(shù)據(jù)。對剩余距離重復上述步驟直至最小距離大于閾值,至此獲得所有的1-2-3確認航跡。 對于已經(jīng)航跡起始成功且未終止的航跡,即可以按照狀態(tài)估計算法對群中心和形狀波門進行預測,然后以預測群中心為中心作形狀波門,完成后續(xù)量測針對各群的歸類劃分,并將等效群中心測量直接分配給產生波門的群航跡,完成后續(xù)群更新迭代計算。設置航跡外推點個數(shù)上限M,在外推點個數(shù)小于M時,若航跡關聯(lián)失敗,用預測值作為更新值進行航跡的維持,一旦外推點個數(shù)達到上限要求,則群航跡終止。 對于預測劃分完后并未被聚類到任何群中的量測,繼續(xù)采用距離劃分的方法進行群分類,直至將所有量測歸類完畢。下一時刻將重新對未起始成功的群中心進行航跡起始判斷,若航跡起始成功,則加入航跡預測與更新過程中。綜上,基于聯(lián)合劃分的群跟蹤流程如圖1所示。 圖1 聯(lián)合劃分法跟蹤流程框圖 設傳感器采樣間隔為T=1 s,觀測時間為0~760 s,傳感器測距誤差均方差為6 m,方位和俯仰測角誤差均方差均為0.001 4 rad,空間目標x、y、z三軸上的初始速度均為3 000 m/s,設置15個誘餌伴隨空間目標飛行,誘餌釋放時刻為初始時刻,誘餌相對彈頭的釋放速度在3~10 m/s按均勻分布隨機選擇。采用考慮地球橢球形狀的標準橢球地球重力模型,其對應ENU坐標系下的目標加速度模型為 其中,x、y、z為ENU坐標系下的目標位置;μ為萬有引力常數(shù);re為地球赤道半徑;J2為地球二階帶諧系數(shù),而 設B為雷達站大地緯度,φ為雷達站地心緯度,令θ=B-φ,ρ=re+z,則 而 其中ω為地球自轉角速度。 仿真生成了雷達對空間密集目標的測量數(shù)據(jù),其ENU坐標系下三軸位置圖如圖2(a)所示,圖2(b)、(c)、(d)分別給出第701~710 s間x、y、z三軸位置隨時間的變化圖,并用16條不同顏色線表示16個目標軌跡。圖3為選取的第100個測量時刻時空間目標在ENU坐標系下的位置分布情況,其中各個顏色代表各目標的分群情況,可見此時空間密集目標共被分為4個群,其中彈頭與距離較近的誘餌被劃分到同一個群中。 圖2 密集群目標的量測位置曲線 圖3 第100 s時的空間目標位置分布情況 為了驗證本章所提算法的有效性,將文中提出的聯(lián)合劃分法與單獨使用距離劃分法后的目標跟蹤結果進行對比分析。圖4是兩種劃分方法下濾波器估計的目標數(shù)目,可見在兩種算法下的空間密集目標均是由一個群逐漸分裂成多個目標群,。距離劃分法各個時刻分群數(shù)目波動較大,這主要是由于目標間距離非常近,從而出現(xiàn)了前后時刻群分割后的各個群中包含的目標數(shù)量會發(fā)生微小變化,而聯(lián)合劃分法中一旦航跡起始成功,將根據(jù)預測進行群劃分,群分割結果相對比較穩(wěn)定。隨著時間的延長,目標群逐步分裂成傳感器能夠識別和跟蹤的多個空間目標,此時目標數(shù)目為彈頭和誘餌的總數(shù)目。 圖4 兩種算法下分群數(shù)目 為了進一步驗證兩種群分割方法對跟蹤結果的影響,采用OSPA距離對估計誤差進行分析,圖5顯示的是兩種劃分算法下濾波器估計的OSPA距離。可見在最初的一段跟蹤時間內兩種算法下跟蹤的OSPA誤差相差不大,這是由于此時目標均被劃分為一個群,但是隨著群的逐漸分裂,聯(lián)合劃分法下的OSPA距離誤差略小于距離劃分法下的誤差,在跟蹤的精度上體現(xiàn)出一定的優(yōu)勢。而且文中算法下誤差的波動也比較小,這是由于距離劃分法中各個群中的目標數(shù)量波動導致等效的群中心位置產生波動,因此跟蹤過程中產生較大的估計誤差,而聯(lián)合劃分法群分割結果相對比較穩(wěn)定,避免了估計誤差的波動。在各個目標已經(jīng)完全分離開的后續(xù)跟蹤階段中,兩種算法的分群都非常穩(wěn)定,誤差精度就基本相同了。圖6顯示的是兩種劃分方法下的單步運行時間,可見文中算法在提高精度的同時整體上具有較好的實時性。 圖5 兩種算法下OSPA距離 圖6 兩種算法下單步運行時間 針對空間密集目標分群問題,提出了距離劃分與預測劃分相結合的聯(lián)合劃分算法,保證了各階段分群的穩(wěn)定性,同時提高了群質心的精度及跟蹤的實時性,有利于后期傳感器對目標的精確預報,具有工程應用價值。后續(xù)工作可進一步研究更為準確的形態(tài)估計模型進一步提高分群的穩(wěn)定性與精確性,同時使算法更加適應復雜的空間作戰(zhàn)環(huán)境。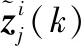
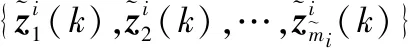
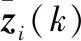
3 形狀預測劃分法
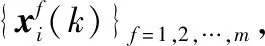
3.1 目標的狀態(tài)估計

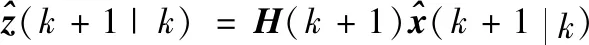

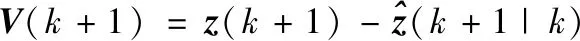
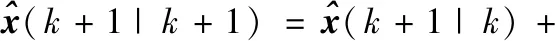
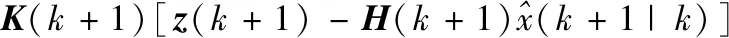
3.2 目標的形態(tài)估計
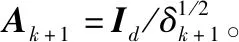
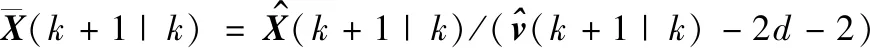
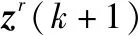
3.3 群中心數(shù)據(jù)的獲取
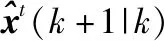
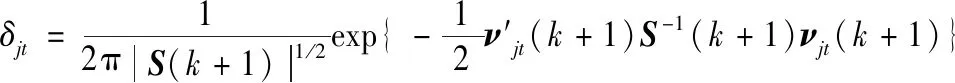
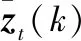
4 群航跡起始與維持
4.1 群航跡起始
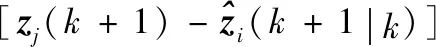
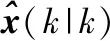
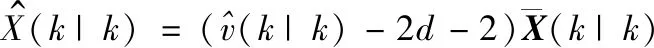
4.2 群航跡維持
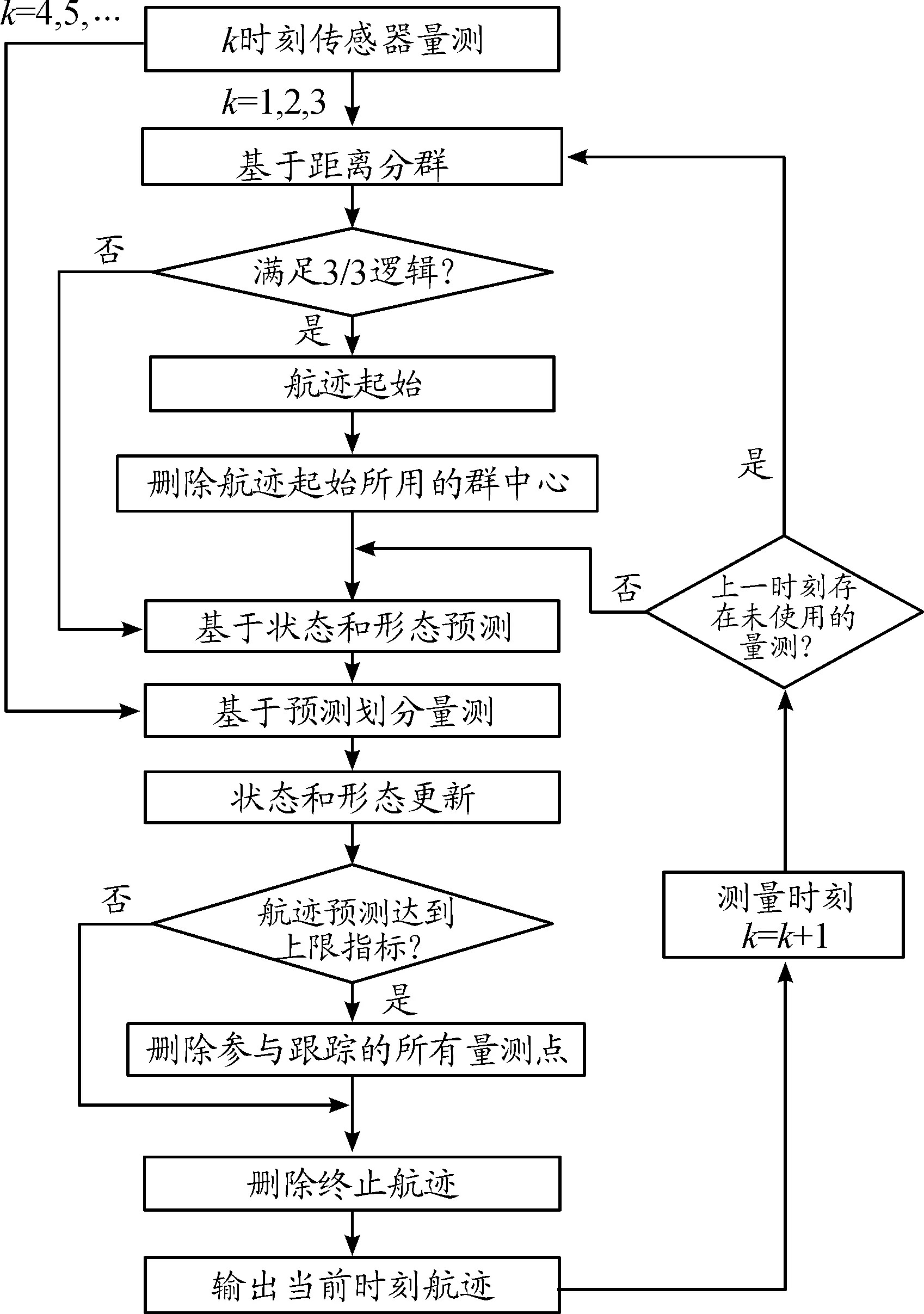
5 仿真分析
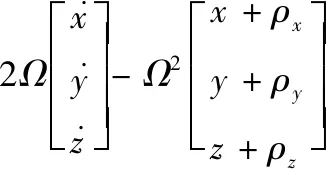
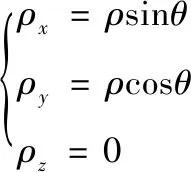
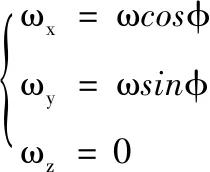
6 結論

