基于權重系數消除和有限控制集優化的雙三相永磁容錯電機快速預測直接轉矩控制

趙 勇 黃文新 林曉剛 姜 文

基于權重系數消除和有限控制集優化的雙三相永磁容錯電機快速預測直接轉矩控制

趙 勇 黃文新 林曉剛 姜 文

（南京航空航天大學自動化學院 南京 211106）

為改善雙三相永磁容錯電機采用傳統預測直接轉矩控制（PDTC）時存在的權重系數整定困難、有限控制集元素數量多以及電壓矢量滾動尋優時間長等問題，該文提出一種基于權重系數消除和有限控制集優化的快速PDTC。首先，根據無差拍直接轉矩磁鏈控制思想，將評價函數中不同量綱的變量等效為相同量綱的電壓矢量，消除了定子磁鏈權重系數；其次，基于永磁容錯電機大電感的特點，提出僅選取零序電壓為零的電壓矢量或者所合成虛擬電壓矢量作為有限控制集元素，不僅消除了零序權重系數，還將有限控制集中的元素從64個減少到19個，同時改善了零序電流的抑制效果；最后設計了一種可一次選出最優電壓矢量的方法，避免了滾動尋優帶來的計算負擔。實驗結果驗證了所提PDTC的可行性和有效性。

雙三相永磁容錯電機 預測直接轉矩控制（PDTC） 權重系數消除 有限控制集優化 快速電壓矢量選擇

0 引言

雙三相永磁電機屬于多相永磁電機的一種，兼具永磁電機轉矩平穩性好、轉矩密度高以及多相電機控制自由度多、容錯性能強的雙重優勢，在航空航天驅動及電力機車牽引等領域備受關注[1]，這些場合對電機的容錯能力要求較高，然而普通雙三相永磁電機不具備短路容錯能力。為使電機具備該能力，需將雙三相永磁電機的定子槽設計為如圖1所示的形狀。圖1電機槽口深而窄，通過大幅度地增大相繞組漏感來提升電機自感，以抑制短路電流；并且采用隔齒繞制各相繞組形式，實現磁隔離、熱隔離及物理隔離[2]，這類電機稱為雙三相永磁容錯電機。

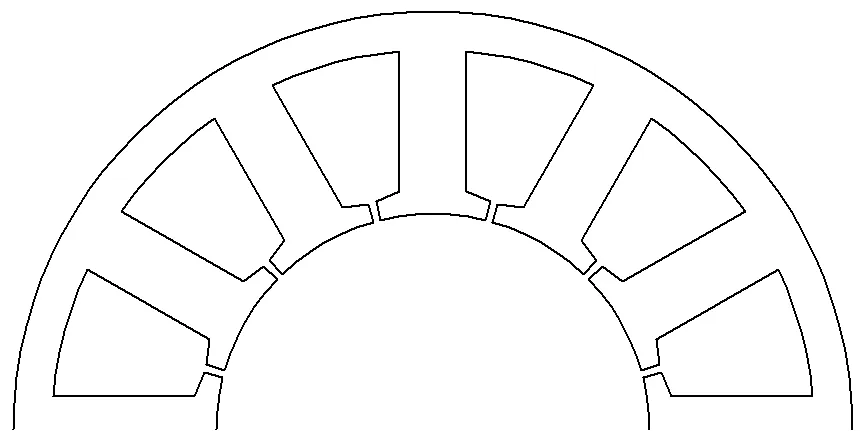
圖1 雙三相永磁容錯電機定子

此外，上述場合通常對電機的電磁轉矩控制要求較高[3]。傳統直接轉矩控制（Direct Torque Control, DTC）因為其快速的轉矩、磁鏈控制能力，可作為雙三相永磁容錯電機具有競爭力的驅動方案。但其缺點是采用了離線計算的最優開關表，未考慮不同轉速、負載的影響，導致轉矩脈動一般較大，同時雙三相電機開關矢量多，最優開關矢量表構建困難，如果考慮零序電流抑制，情況更加復雜。

目前已有眾多文獻致力于優化DTC的上述缺點，其中，將有限控制集預測控制與DTC相結合被證明是有效方案之一[4]。形成的有限控制集預測直接轉矩控制（Predictive Direct Torque Control, PDTC）不但保留了DTC的快速響應性，還在選擇開關狀態時考慮了轉速、負載及零序分量的影響，同時僅需構建形式較為簡單的評價函數，無需構建最優開關矢量表。但應用于雙三相永磁容錯電機時，PDTC仍然存在幾點問題。

一是權重系數選取復雜。由于同時兼顧基波平面及零序平面多個不同變量的控制，需要引入多個權重系數，雙三相永磁容錯電機的權重系數整定更加困難[5]。對于權重系數的處理，文獻[6]提出了基于模糊控制的權重系數在線整定方案，針對電機的不同運行狀態，實時計算相應的權重系數；文獻[7]則構造了二次型價值函數，成功地將多個權重系數整合成一個權重系數的求解。但這兩種方案會進一步增加控制芯片的計算壓力。因此，越來越多的學者主張消除權重系數，如文獻[8-9]將對轉矩和磁鏈的控制等效為對定子磁鏈的控制，由于等效控制目標的量綱相同，不再需要權重系數；文獻[10]將評價函數設計為對轉矩的控制；文獻[11]則直接采用了電流預測控制，構建時只包含電流，也避免了權重系數的存在。但文獻[8]不適用于凸極永磁電機，文獻[9, 11]沒有涉及零序電流的抑制。

二是雙三相永磁容錯電機有限控制集中元素數量較多。相比于三相電機只有8個電壓矢量，雙三相電機采用雙三相逆變器驅動時，電壓矢量增至64個，導致PDTC計算負擔較重。文獻[12]只選取了6個最大矢量進行合成，減少了有限控制集元素數量。文獻[13]在六相異步電機驅動系統中采用了部分矢量合成的虛擬矢量，實現了減小計算負擔的目的，但在一定程度上影響了電機性能。因此文獻[5]在文獻[13]基礎上增加了虛擬矢量的個數，改善了電機轉矩性能。而文獻[14]為了抑制共模電壓，選取了共模電壓為零的矢量，矢量數量減少，但是降低了母線電壓利用率。上述文獻中的方案雖然精減了電壓矢量，卻犧牲了電機驅動系統的部分性能。

三是滾動優化循環次數多，計算負擔大。預測控制采用了將有限控制集中元素滾動代入評價函數尋找最優值的方式，元素越多，滾動計算次數越多。通過扇區劃分和對電壓誤差量的比較，文獻[11]只需一次預測即可選出最優電壓矢量；文獻[15]通過劃分區域優化了有限控制集，減少了滿足條件的矢量，縮短了尋找最小價值函數值的時間。但文獻[11, 15]未考慮零序電流的抑制。文獻[8, 16]剔除了部分矢量，選擇剩余的矢量建成了優化離線開關表，節省了計算時間，但仍然需要多次在線滾動計算，計算負擔尚需進一步減小。

為解決上述問題，本文提出了一種基于權重系數消除和有限控制集優化的雙三相永磁容錯電機快速PDTC方法。首先，以數學模型更為一般的凸極式永磁電機為研究對象，利用無差拍直接轉矩磁鏈控制思想，將預測變量等效為量綱一致的電壓矢量，消除了定子磁鏈權重系數；其次，根據永磁容錯電機漏感大的特點，僅選用零序電壓為零的電壓矢量或者合成虛擬電壓矢量來抑制零序電流，消除了零序權重系數并優化了有限控制集中的元素；再次，提出了一種快速最優電壓矢量選擇方法。最后搭建了雙三相永磁容錯電機測試平臺，實驗結果表明所提策略有效可行。

1 預測直接轉矩控制原理

1.1 雙三相永磁容錯電機數學模型

雙三相永磁容錯電機驅動系統如圖2所示。其中，ACE相和BDF相繞組負端分別連接成一個中性點N1和N2，A、B相之間相差60°，DC為母線電壓。參與機電能量轉換的基波分量坐標系如圖3所示，其中，A~F分別對應電機各相繞組軸線，αβ為兩相靜止坐標系，α軸與A相軸線位置重合，dq軸是與轉子同步的兩相旋轉坐標系，其中，d軸與α軸之間電角度差為r，為定子磁鏈定向坐標系，與d軸夾角為電角度，即轉矩角；與α軸夾角為電角度s。另外，r、s、s、s分別為轉子、定子磁鏈矢量、定子電流和電壓矢量，其在不同軸上的投影分別用對應的下標表示，r為轉子旋轉角速度。

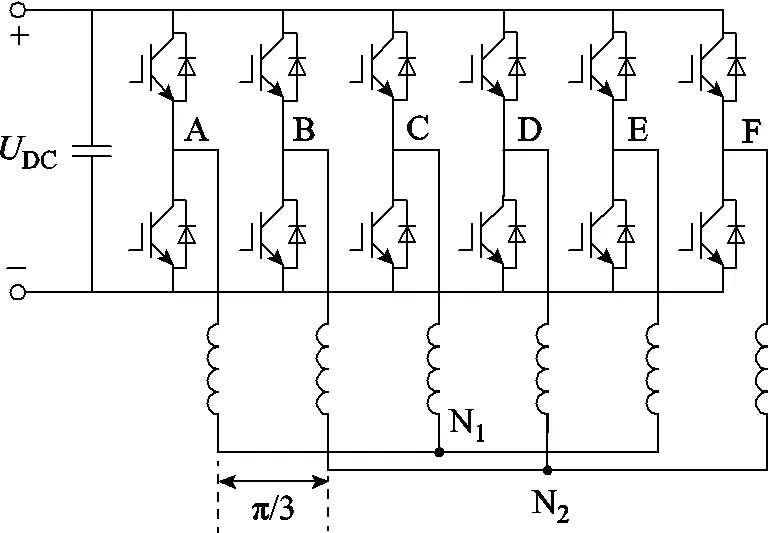
圖2 雙三相永磁容錯電機驅動系統

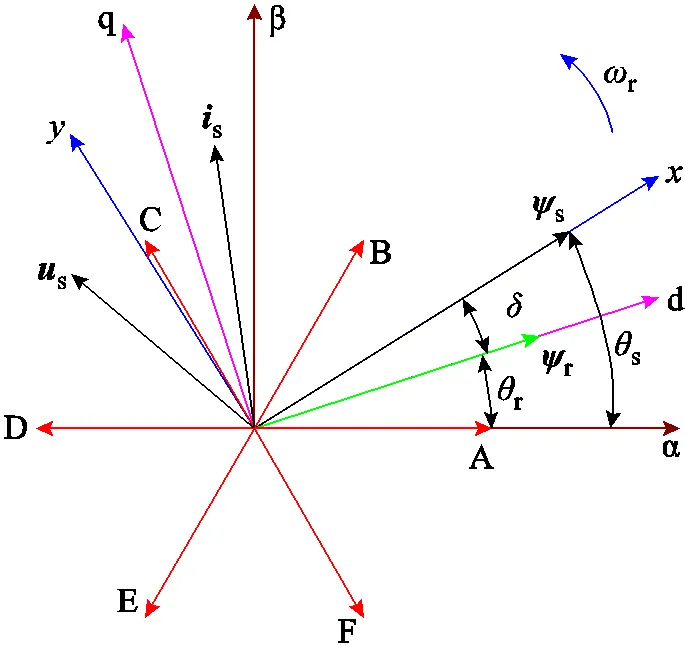
圖3 基波分量坐標系

為了實現雙三相永磁容錯電機的解耦，根據矢量空間解耦理論推導得到解耦矩陣如式（1）所示[12]。矩陣的前兩行對應參與能量轉換的αβ軸分量，除此之外，還有4個零序分量，分別表示為1~4，這些分量不參與機電能量轉換，但是會增加電機相電流的諧波含量和損耗，因此希望將其控制為0。

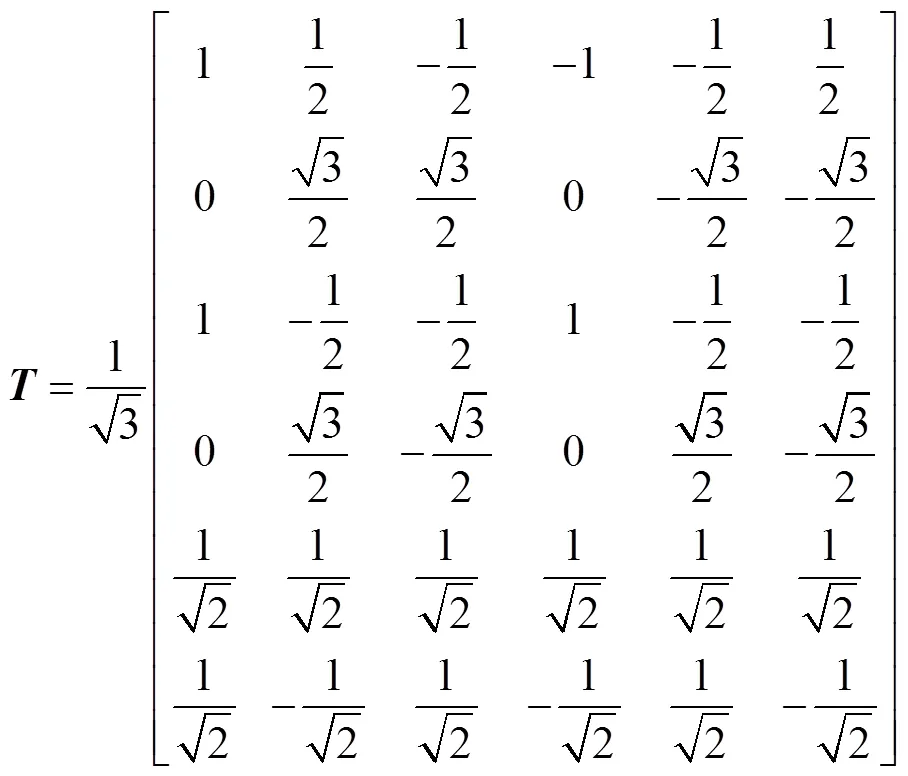
dq軸下電機的磁鏈、電壓和轉矩方程分別為

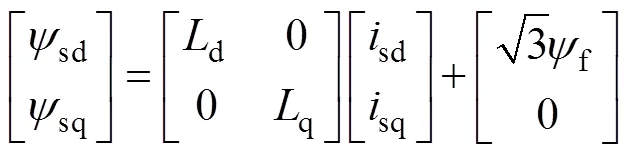
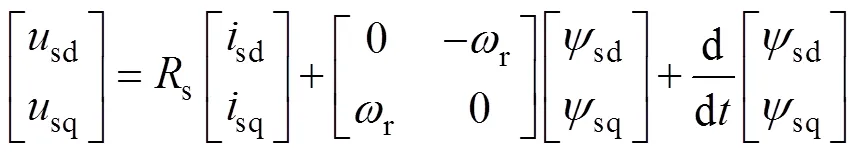
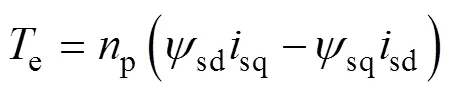
式中，d、q分別為d、q軸電感；f為轉子磁鏈；p為電機極對數。

零序分量的磁鏈和電壓方程分別為

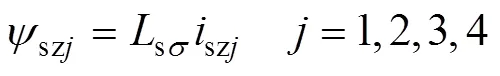
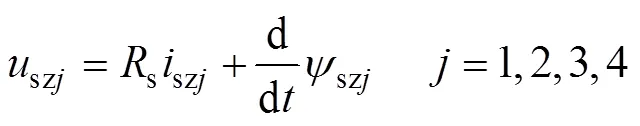
式中，sσ為電機相繞組漏感；s為定子相繞組電阻；szj、szj分別為零序電流和磁鏈分量，由于雙三相電機采用雙中性點的連接模式，ACE相和BDF相的相電流之和為零，由式（1）的最后兩行可知，sz3和sz4自然為0，故只需要考慮將sz1和sz2控制為0。

1.2 雙三相永磁容錯電機傳統預測直接轉矩控制

按照傳統PDTC思想，除對電機的轉矩、磁鏈進行控制，根據1.1節的分析可知，還需要加入對sz1和sz2的抑制。因此評價函數為[5]

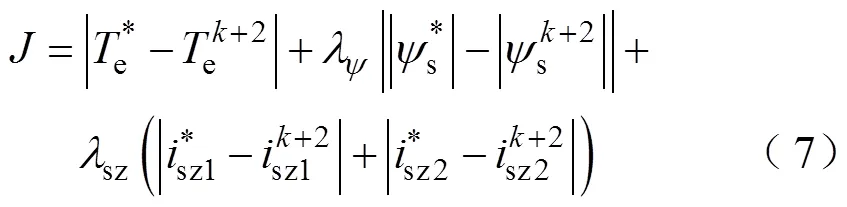
式中，和sz分別為定子磁鏈和零序權重系數。

當圖1中六個橋臂分別取不同值時，可產生64個電壓矢量，按照A~F從高到低進行二進制計數，它們在αβ平面及12平面的電壓分量分別如圖4和圖5所示。式（7）中，+2時刻各電壓開關量對應的轉矩、磁鏈可根據當前時刻的狀態量、式（2）~式（4）、圖4及其他相關電機方程進行預測；而零序電流則根據式（5）、式（6）和圖5進行預測。

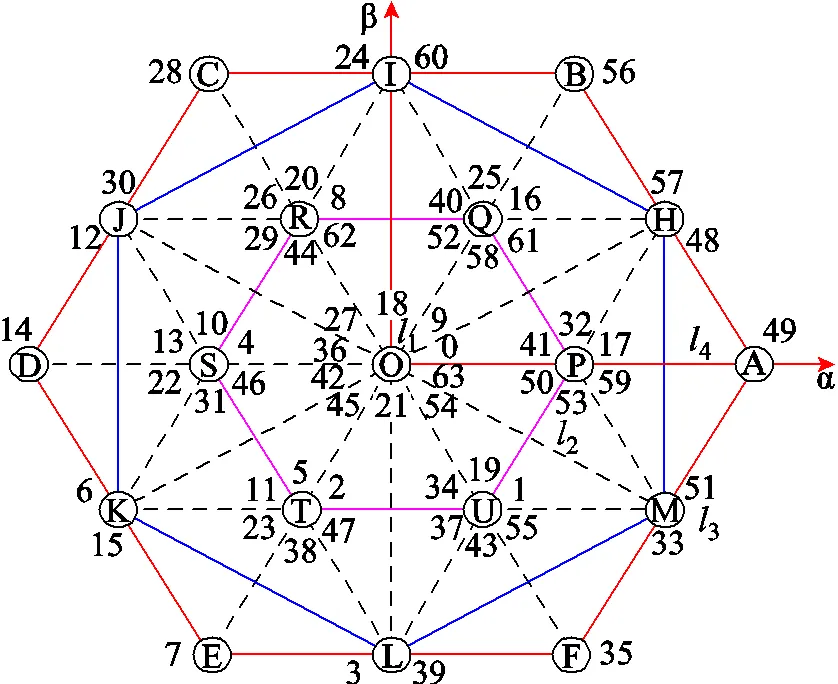
圖4 αβ平面定子電壓矢量圖

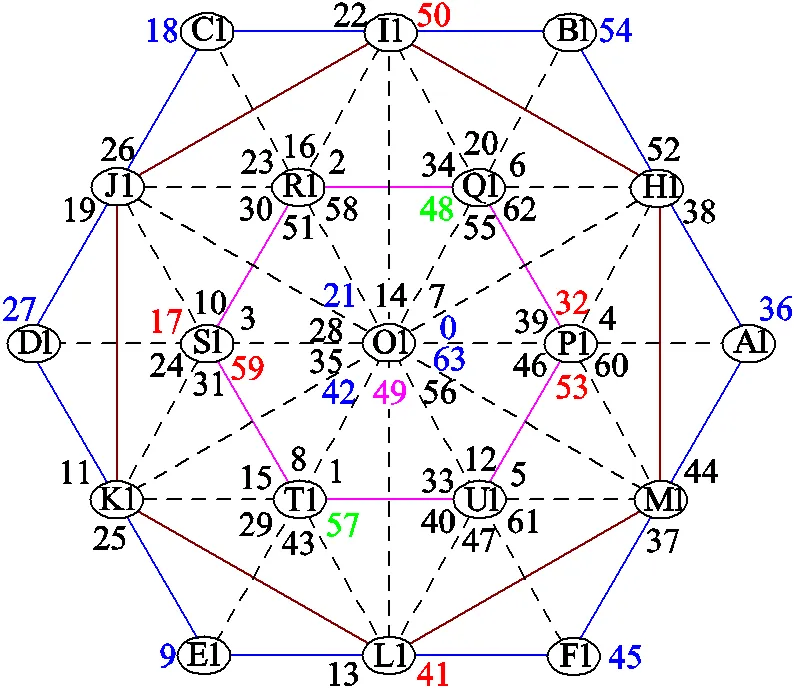
圖5 z1z2平面定子電壓矢量圖

1.3 所提雙三相永磁容錯電機預測直接轉矩控制

傳統PDTC雖然可以實現轉矩、磁鏈及零序電流的控制，但存在問題有：①評價函數中不同量綱的變量較多，需要引入多個權重系數，使得本就復雜的權重系數選取更加困難；②有限控制集中元素數量較多，計算量大；③滾動尋優時循環次數多，計算負擔重。為解決上述問題，本文提出了一種基于權重系數消除、有限控制集優化和快速電壓矢量選擇的PDTC。其中，1.3.1節給出了所提權重系數消除方案的第一步；1.3.2節給出了所提權重系數消除方案的第二步和有限控制集優化方案；1.3.3節給出了所提快速電壓矢量選擇方案。

1.3.1 定子磁鏈權重系數消除

本節主要介紹所提權重系數消除方案的第一步，即優化評價函數中的評價變量，將不同量綱的變量等效為相同量綱的變量，達到消除λ的目的。

將式（2）代入式（4）可以得到

而

因此，轉矩和磁鏈均可表示為只與變量sd和sq相關的表達式，也就是說控制好d軸、q軸磁鏈，就等效于控制好了磁鏈幅值和轉矩。而根據式（5），零序電流與零序磁鏈成正比，因此控制好零序磁鏈也等效于控制好了零序電流，故評價函數式（7）可等效為

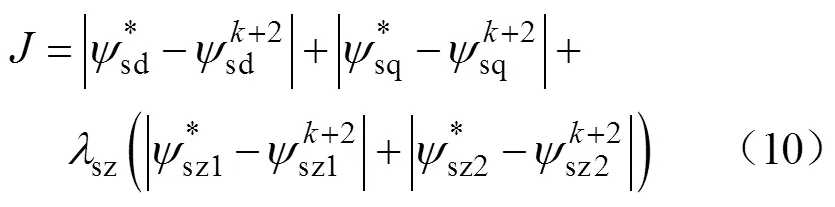
式（10）中，評價函數中所有的量綱均為磁鏈，故只需要在dq軸磁鏈和零序磁鏈間引入一個零序權重系數sz即可，從而消除了，避免了多個權重系數的存在。式（10）的具有實現過程如下。

1）預測每個電壓矢量在+2時刻的d、q軸磁鏈

將式（3）離散化可知+1時刻的d、q軸磁鏈為

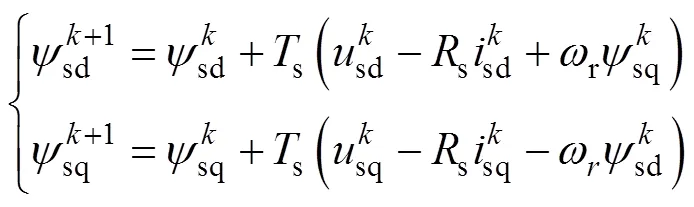
式中，s為控制周期，且

通過式（2）得到+1時刻的d、q軸電流分別為

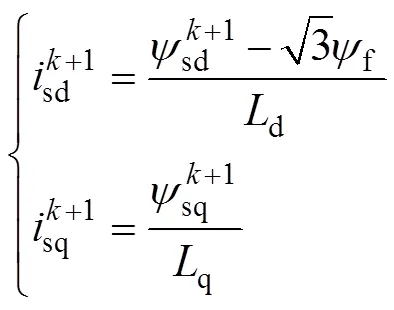
類似式（11），推導得+2時刻d、q軸磁鏈為

2）預測每個電壓矢量在+2時刻的零序磁鏈

根據式（5）、式（6）得到+1時刻零序實際磁鏈為

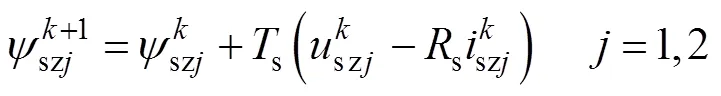
將式（15）代入式（5）得到此時的零序電流為

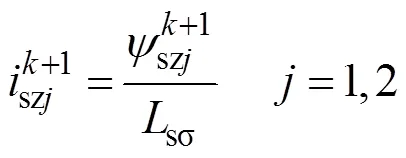
類似式（15），得到+2時刻零序實際磁鏈為

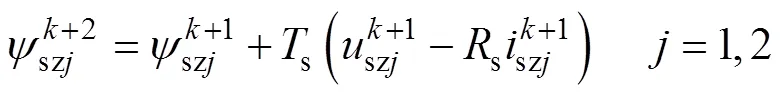
3）求解d、q軸參考磁鏈

相比于+2時刻d、q軸磁鏈預測值和零序磁鏈預測值容易求得，d、q軸磁鏈參考值卻難以求得，這里給出了d、q軸參考磁鏈的求解。

根據圖3可得

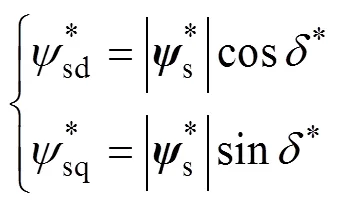
故只需求出轉矩角就能準確跟蹤d、q軸磁鏈，而轉矩角的表達式為[17]

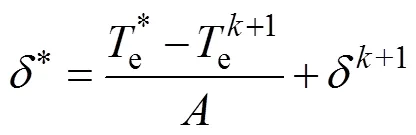
其中

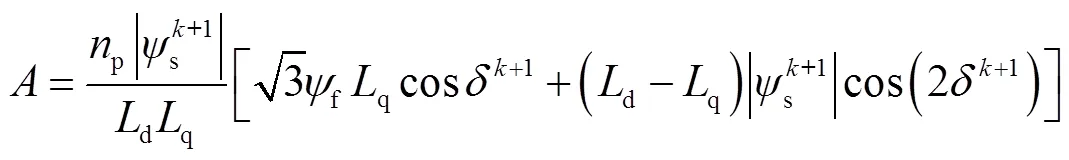
而+1時刻轉矩、磁鏈幅值和轉矩角分別為

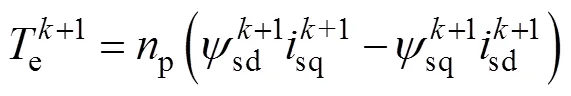
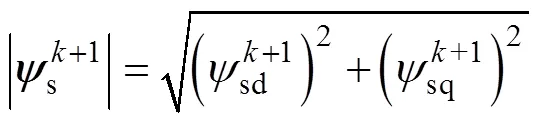
4）零序磁鏈參考值

根據式（5），零序電流與零序磁鏈成正比，故欲將零序電流控制為0，則零序磁鏈參考值應為0。

5）將各矢量對應的量代入評價函數滾動尋優

至此為式（10）的預測過程，其在消除的過程中，考慮了電機凸極效應和電阻的影響，適用性更強。但缺點是：除預測每個開關矢量在下兩個時刻對應的d、q軸磁鏈和零序磁鏈，還需要計算dq軸磁鏈參考值，計算負擔重。而如果能將磁鏈預測轉變為電壓矢量的預測，然后直接與圖4和圖5中的電壓矢量進行對比，將更加直接簡便。具體過程如下。

對于基波平面，這里采用軸坐標系作為中間變量，根據無差拍直接轉矩磁鏈控制思想得

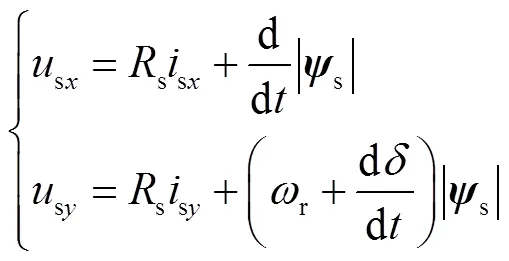
離散化后得

其中

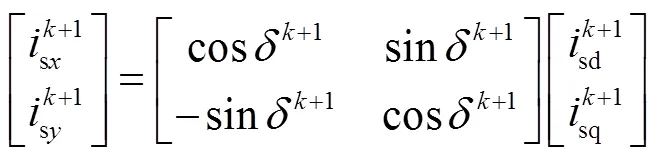
將式（11）~式（13）及式（19）~式（23）代入式（25）即可求出軸參考電壓值，根據軸電壓與α、β軸電壓的關系，求出α、β軸參考電壓為

而αβ軸實際電壓可根據圖4得到。

對于零序平面，由式（5）與式（6）得

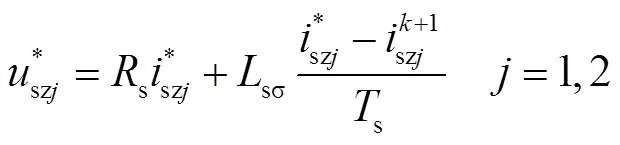
式（28）中，目標零序電流為零；實際零序電壓可由式（1）和圖5得到。根據上述分析，設計評價函數為

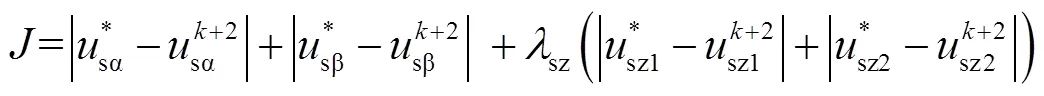
與式（7）相比，評價函數式（29）不僅完成了評價變量量綱的統一，還成功地將預測變量等效為更直接的電壓量，從而消除了權重系數，簡化了評價過程、減輕了計算負擔。

1.3.2 零序權重系數sz消除以及有限控制集優化

式（29）雖然實現了評價函數的優化和定子磁鏈權重系數的消除，但仍然存在的問題是：①零序權重系數sz依舊存在，仍需要對其進行復雜的整定；②需要將64個電壓矢量代入，進行在線滾動尋優，計算負擔重。本節將致力于解決以上兩個問題。

1.3.1節通過統一變量量綱實現了的消除，但由于控制目標重要程度不同，導致無法消除sz。而從式（28）可知，為使實際零序電流為零，需將零序電壓參考值設為0；而如果實際零序電壓平均值也為0，則式（29）中后兩項恒等于零，sz就可以消除。根據式（6）構建如圖6所示的零序電流szj(=1,2)等效電路，電路中僅包含了零序電壓、相電阻和漏感。由圖6可知，僅需使szj在一個控制周期中的平均值為0，即可滿足上述要求，而要使szj平均值為0，可直接選擇零序電壓為0的電壓矢量或者通過電壓矢量合成的方式獲得。

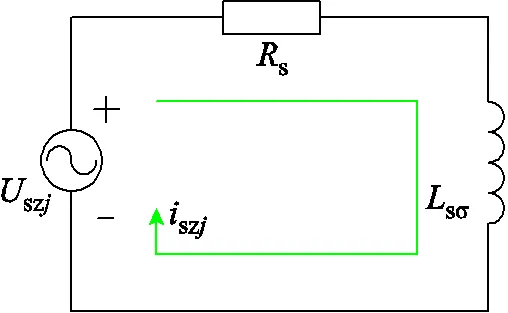
圖6 零序電流等效電路

具體方法為：在保證圖4電壓矢量圖完整的前提下，在每個頂點上選取一個零序電壓為零的電壓矢量，或者兩個零序電壓方向相反的電壓矢量合成零序電壓為0的虛擬電壓矢量，以抑制零序電流，從而消除sz，此為權重系數消除方案的第二步。

文獻[12]研究表明采用合成虛擬電壓矢量時，死區及開關管的開通關斷會產生不可控的電壓矢量，雖然時間較短，伏秒積數值小，但由于普通電機零序電流環時間常數較小，故會產生較大的零序電流。而本文研究的是雙三相永磁容錯電機，大漏感導致其自感較大。正是由于這一特點，上述因素造成的零序電流數值較小，文獻[12]所提的影響在本電機中無需考慮。因此雙三相永磁容錯電機可采用兩矢量合成虛擬電壓矢量的方法抑制零序電流。

同時基于上述分析，本文提出了雙三相永磁容錯電機的有限控制集優化方法。圖4中雖然共有64個電壓矢量，但是在αβ平面上只形成19種不同情況，按照幅值分為1~4四層。并且這19個點均存在零序電壓為0的電壓矢量，或者至少兩個零序電壓相反的電壓矢量。其中，1層只存在一個點，即O點，滿足該點的矢量有10個，但是只有四個產生的零序電壓為零，即編號為0、21、42、63的矢量，另外6個矢量產生的零序電壓處于最外層，它們幅值相等，但兩兩方向相反（36與27，54與9，18與45分別相反）；2層存在6個點，即P、Q、R、S、T、U，每個點上有6個矢量，以P點為例，包含矢量17、32、41、50、53和59，矢量17、59的零序電壓與32、53的零序電壓大小相同，方向相反，矢量41與50的零序電壓大小相等，方向相反；3層也包括6個點，即H、I、J、K、L、M，每個點上有兩個矢量，以H點為例，矢量48與57的零序電壓大小相等，方向相反；而4層同樣有6個點，每個點上一個矢量，所有矢量產生的零序電壓均為0。

根據上述分析，選出如圖7所示的電壓矢量組合作為有限控制集的元素，其中，2和3層所在六邊形頂點上的電壓矢量為兩個實際矢量所合成的虛擬電壓矢量。以頂點H上的電壓矢量為例，其虛擬電壓矢量由48和57合成，其余虛擬電壓矢量的合成方式類似，這里不再贅述。

圖7 優化后的αβ平面定子電壓開關矢量圖

采用本節所提的sz消除和有限控制集優化方案后，只需要根據參考電壓矢量的αβ分量在圖7中的19個矢量組合中選擇最適合的矢量組合即可同時實現轉矩、磁鏈以及零序電流的控制，無需再遍歷64個矢量，也可將評價函數簡化為

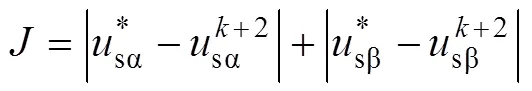
與式（29）相比，式（30）中只存在αβ軸電壓分量，為兩個相同量綱、重要程度一致的變量，因此無需再引入任何權重系數，也就是說實現了權重系數的完全消除。此外，有限控制集的元素從64個縮減到19個，零序電流也可得到相應的抑制。

1.3.3 快速電壓矢量選擇

1.3.1節和1.3.2節所提策略解決了傳統PDTC的前兩個問題，但即使如此，在每個控制周期內仍然需要循環19次。為了進一步減小計算負擔，本節提出了一種快速電壓矢量選擇方案。

如圖7中所示，電壓矢量被劃分為12個扇區：S1~S12，每個扇區均包含1~4層一個點。如果按照扇區劃分的方法，在確定參考電壓矢量的扇區后，繼續采用滾動尋優的方式尋找最優電壓點，需要4次，仍然較多，本節旨在進一步減少尋優次數。

圖7中，奇數扇區均可通過旋轉的方式對應到扇區S1，而偶數扇區均可通過先旋轉到扇區S2，再對稱到扇區S1，因此所有扇區的尋優完全變換成了扇區S1的尋優。

再對扇區S1進行分區，如圖8所示，兩條虛線1、2將扇區1分為三個部分，其中，1、2分別為OP、PA的中垂線。參考電壓終點落于1左側區域時，更靠近O點，此時應選擇O點上的矢量；參考電壓終點在1與2中間區域時更靠近P點或者M點，并且如果矢量在VX上側，選擇P點，在VX下側，選擇M點，其中VX為PM的中垂線；同樣參考電壓終點在2右側時，如果在XY上側，選擇A點，在XY下側，選擇M點，XY為AM的中垂線。因此不需要循環尋優，而只需要進行一次查找即可得到最優點，最后根據參考電壓矢量實際所在扇區選出實際對應的點和矢量。

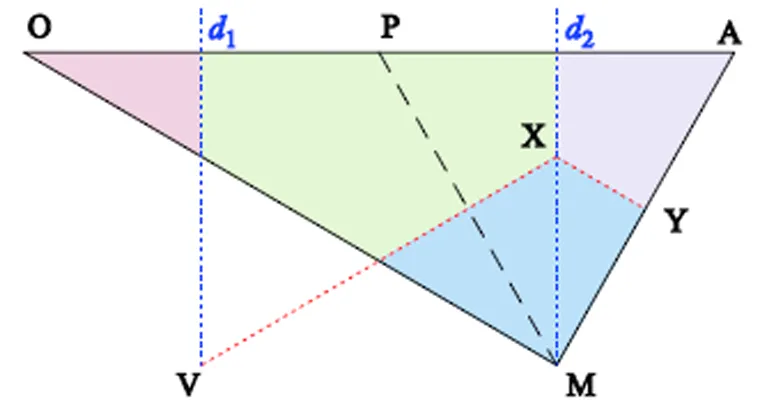
圖8 快速電壓矢量選擇示意圖

綜上，快速電壓矢量選擇的步驟為：

1）根據參考電壓矢量的αβ分量判斷所處扇區。

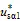
當參考電壓位于奇數扇區時（S為實際扇區）

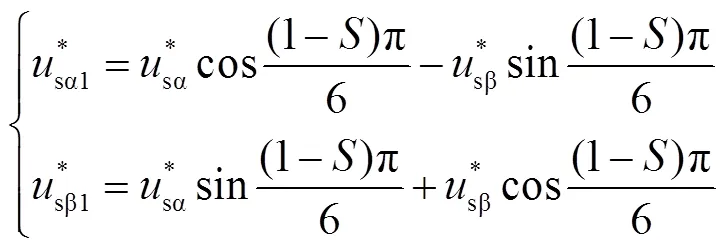
參考電壓位于偶數扇區時

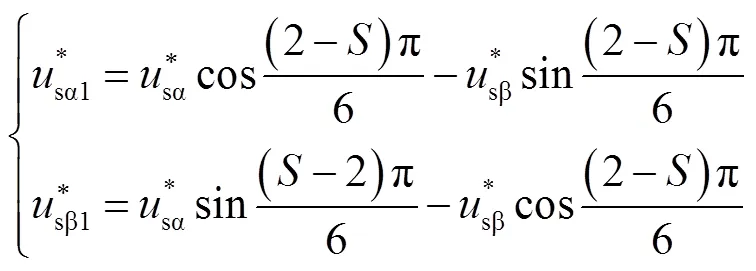
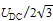
4）根據實際所處扇區及所選點，選出實際對應點和矢量，具體關系見表1。

表1 扇區S1上的點與實際點和矢量的對應關系

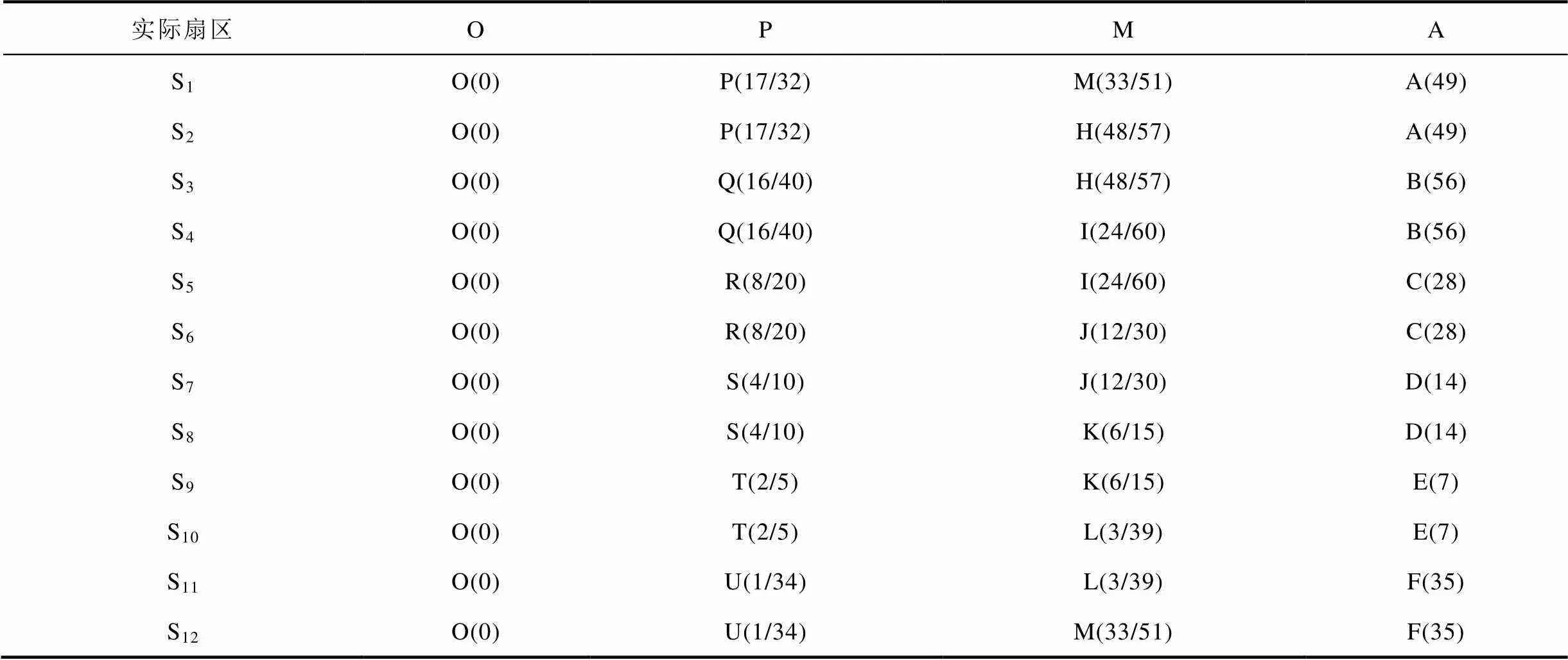
Tab.1 The relationship between actual points and voltage vectors and points in S1

1.4 所提雙三相永磁容錯電機PDTC系統結構

所提雙三相永磁容錯電機PDTC框圖如圖9所示。通過檢測到的時刻電流，坐標變換后代入式（2）中，計算得到時刻dq軸磁鏈；根據時刻實施的開關狀態，得到相應的dq軸電壓，與角速度一起代入式（11）中進行延時補償，預測+1時刻dq軸磁鏈及其幅值，結合式（13）可得+1時刻電流，以式（21）計算+1時刻轉矩，采用式（23）得到此時的轉矩角。系統外環為轉速閉環，速度調節后計算出目標轉矩，將目標轉矩、給定磁鏈幅值，+1時刻轉矩、磁鏈、電流和轉矩角，轉子位置、轉速，代入式（25）~式（27）得到定子α軸、β軸定子參考電壓；最后根據定子參考電壓判斷扇區，采用快速方案選擇矢量，進行矢量合成，從而控制整個系統。

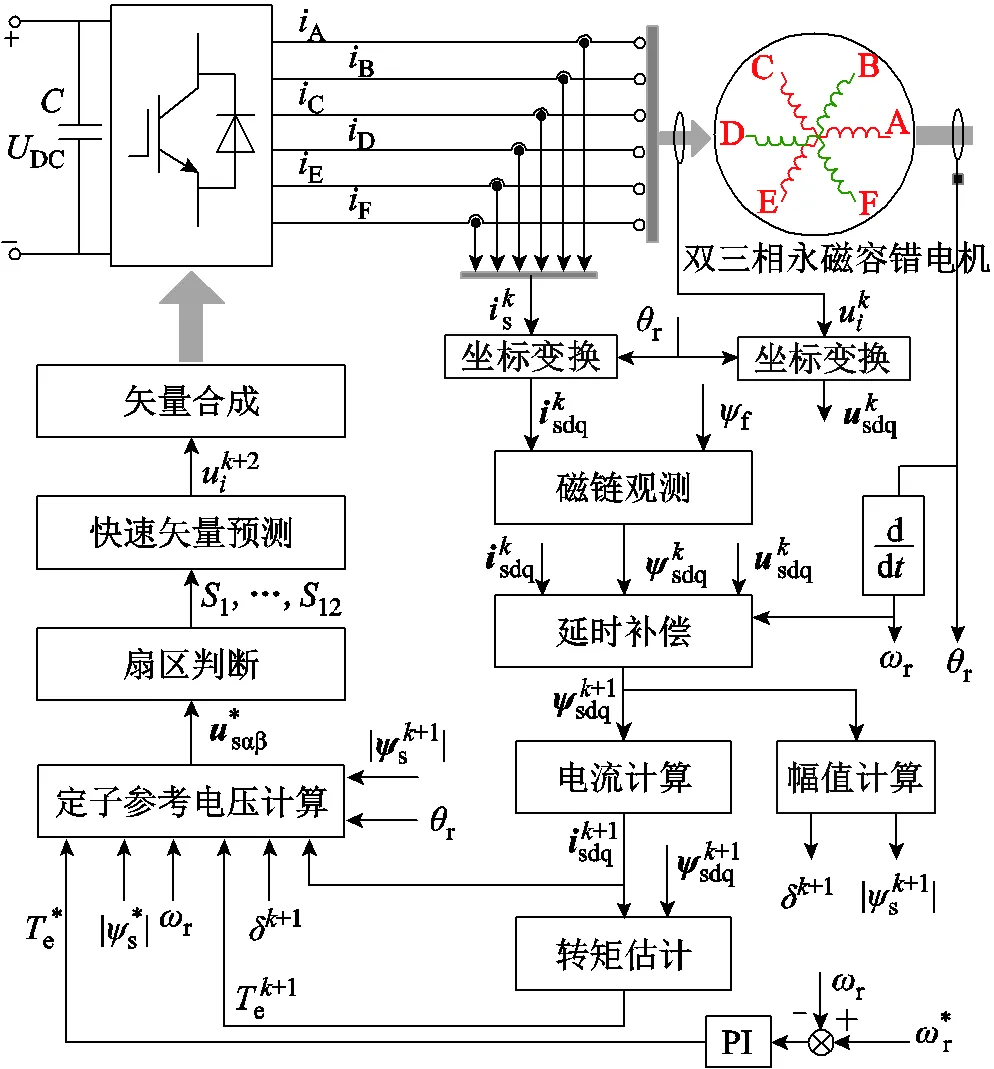
圖9 雙三相永磁容錯電機PDTC驅動系統框圖

2 實驗驗證

2.1 實驗平臺與參數

本文所采用的雙三相永磁容錯電機部分參數見表2。基于該電機，搭建了如圖10所示的實驗平臺。轉子同軸安裝了旋轉變壓器進行位置檢測，負載電機為一異步電機，采用通用變頻器驅動。所用雙三相永磁容錯電機的逆變器和控制單元分別如圖10中③、④所示，逆變器直流母線電壓100V，控制單元的控制周期為80μs。

表2 電機參數

Tab.2 Parameters of machine

圖10 實驗平臺

①—通用變頻器 ②—加載平臺 ③—逆變器 ④—控制單元

Fig.10 The experimental system

2.2 穩態性能實驗

為充分研究系統的穩態性能，本文分別對具有所提定子磁鏈權重系數消除方案（以下稱為PDTC1），具有所提定子磁鏈權重系數消除、零序權重系數消除和有限控制集優化方案（以下稱為PDTC2）以及具有所提定子磁鏈權重系數消除、零序權重系數消除和有限控制集優化、快速電壓矢量選擇方案（以下稱為PDTC3）的三種策略在200r/min、500r/min和1 000r/min下帶額定負載進行了實驗，三種策略的對比見表3。對于PDTC1，已根據sz對轉矩、磁鏈和零序電流的不同影響效果，為式（29）選擇了合適的sz。具體實驗結果如圖11~圖13所示。

表3 三種控制策略對比

Tab.3 Comparisons of three control strategies

上述實驗結果顯示，PDTC1在200r/min、500r/min和1 000r/min情況下均能實現對轉矩轉速的有效控制，表明所提定子磁鏈權重系數消除方案可行有效，且穩定性較好。PDTC2的穩定運行則證明了所提零序權重系數消除方案的穩態性能，另外相比于PDTC1，PDTC2具有更小的零序電流，因此其相電流幅值更小，帶載能力更強。同時對三種情況下的A相電流進行了諧波THD分析，結果如圖13所示。同樣，PDTC2的相電流諧波含量遠低于PDTC1，說明所提選取零序電壓為0的電壓矢量或者合成虛擬電壓矢量對抑制雙三相永磁容錯電機的零序電流作用明顯。此外，PDTC2和PDTC3的轉矩脈動小于PDTC1，則是因為式（30）相比于式（29）沒有零序變量的預測，得到的αβ軸最優電壓矢量更接近于αβ軸參考電壓，對轉矩磁鏈的控制效果更好，故轉矩脈動更小。表4給出了三種策略的計算時長，PDTC2時長相比于PDTC1縮短了約23%，證明有限控制集優化策略可有效降低計算壓力，而與PDTC2相比，PDTC3的零序電流、諧波含量與前者相當，但是計算時間比PDTC2又再次縮短了22%，體現了所提快速電壓矢量選擇方案的顯著效果。

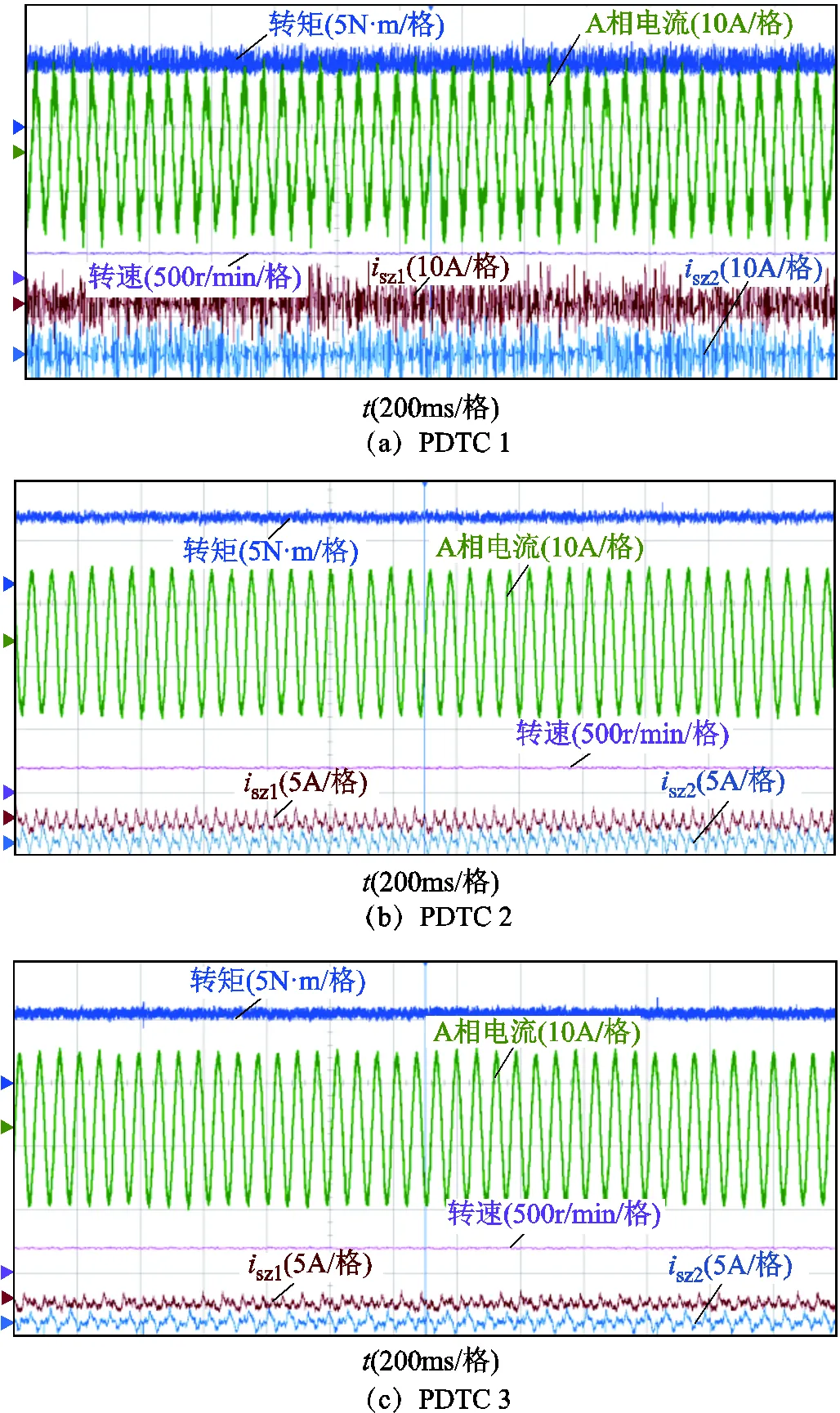
圖11 200r/min穩態實驗

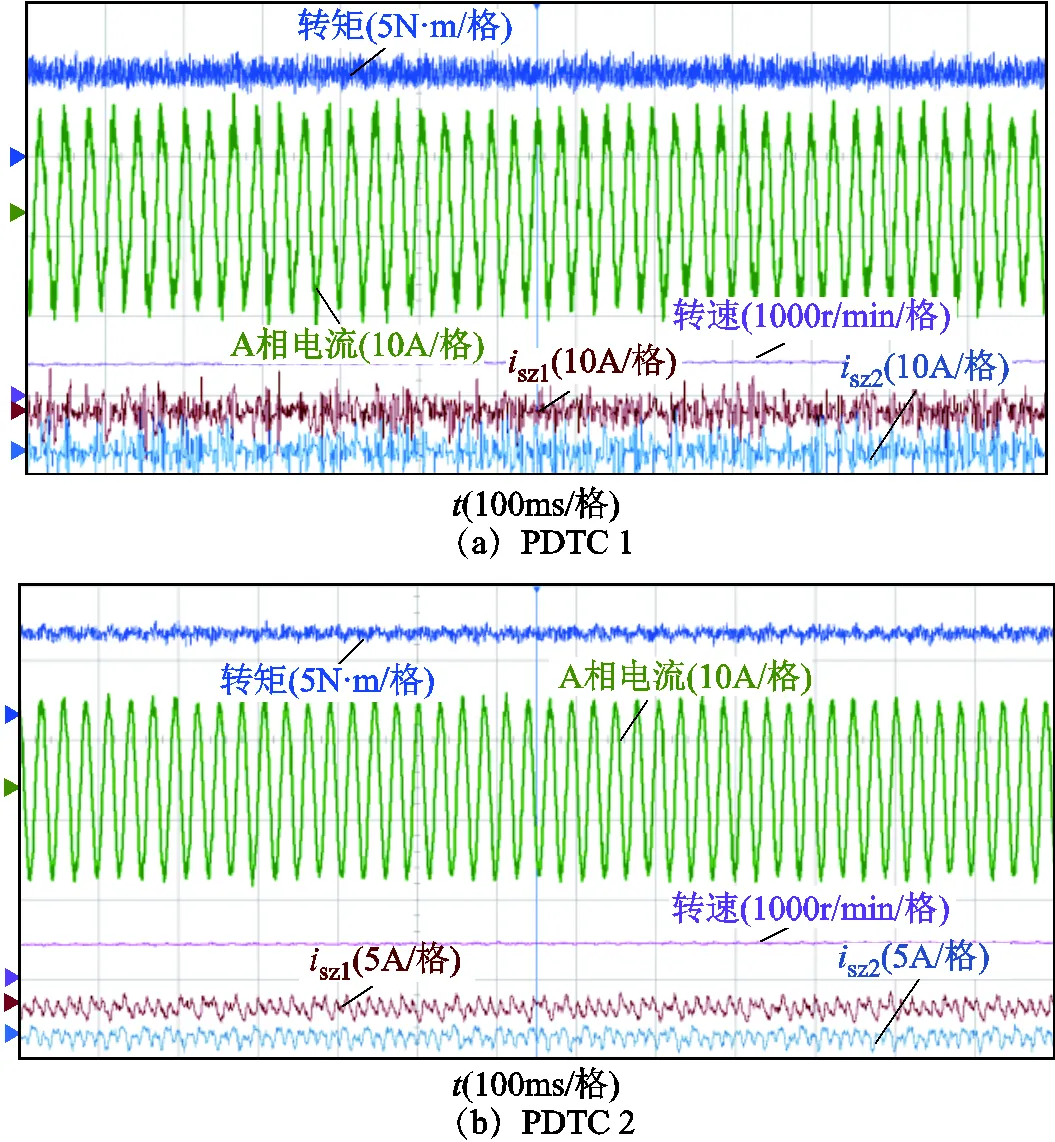
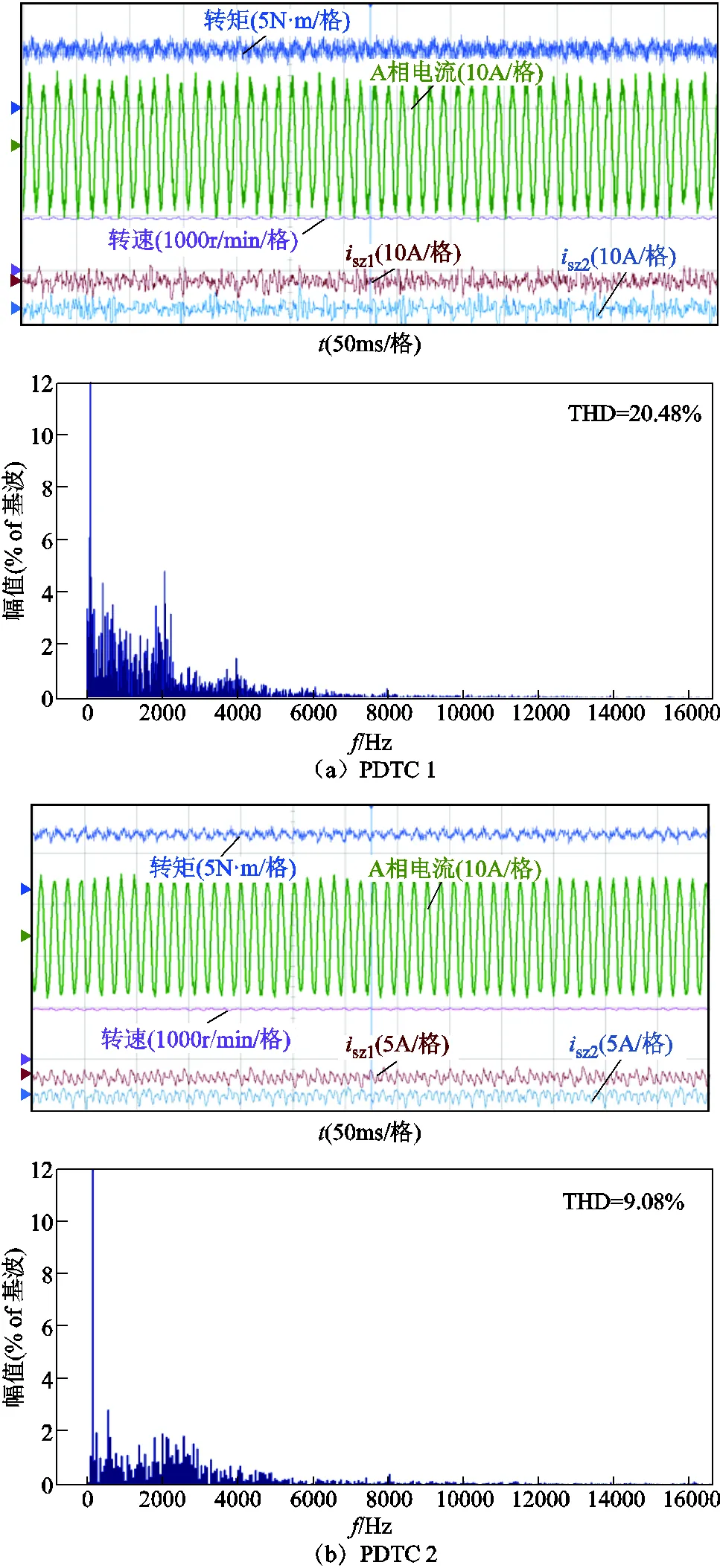
表4 計算時長對比

2.3 動態性能實驗

為了驗證所提策略的動態性能，進行了額定1 000r/min轉速下的動態實驗，如圖14所示。負載電機從施加空載直接階躍到施加額定負載。實驗表明，三種策略均能快速地跟蹤突變的負載，說明所提權重系數消除和有限控制集優化方案具有較好的動態性能。同時三種策略下零序電流均能穩定在0附近，且PDTC2和PDTC3相比于PDTC1零序電流更小，證明所提選取零序電壓為0的電壓矢量或者合成虛擬電壓矢量減小零序電流策略在動態過程中也能保持對零序電流良好的抑制效果。

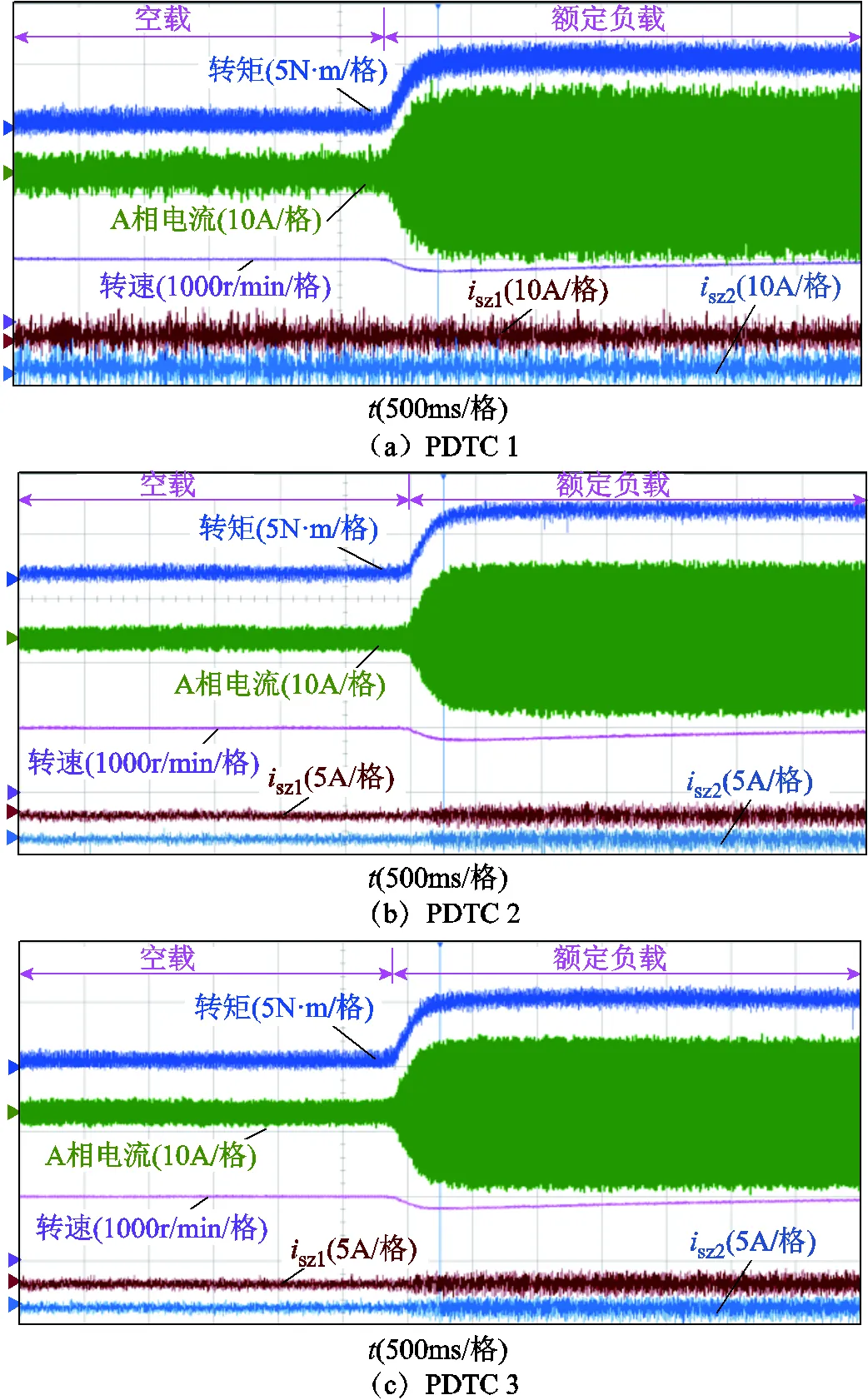
圖14 1 000r/min動態性能實驗

3 結論

本文針對雙三相永磁容錯電機提出了一種基于權重系數消除和有限控制集優化的快速電壓矢量選擇預測直接轉矩控制，并采用實驗對所提策略進行了驗證，結果表明：

1）所提定子磁鏈權重系數消除方案可將評價函數中的變量等效為量綱一致的電壓矢量，并消除定子磁鏈權重系數。

2）所提零序權重系數消除和有限控制集優化方案可成功消除零序權重系數sz，免去繁瑣的權重系數校正過程；優化有限控制集元素數量，減輕計算負擔；并且可以有效地控制零序電流大小，具有較好的穩態以及動態性能。

3）所提快速電壓矢量選擇方案，省去了循環尋優過程，只需要一次即可找出最優的點和矢量，極大地節省了計算時間。

[1] 魏永清, 康軍, 曾海燕, 等. 十二相永磁電機驅動系統的容錯控制策略[J]. 電工技術學報, 2019, 34(21): 4467-4473. Wei Yongqing, Kang Jun, Zeng Haiyan, et al. Fault-tolerant control strategy for twelve-phase permanent magnet synchronous motor propulsion system[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4467-4473.

[2] Jiang Xuefeng, Wang Shaoshuai, Li Qiang, et al. Design and optimization of dual-winding fault-tolerant permanent magnet motor[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(1): 45-53.

[3] 楊建飛, 曹偉, 李德才, 等. 兩相導通無刷直流電機直接轉矩控制零電壓矢量特性分析[J]. 電工技術學報, 2019, 34(23): 4948-4956. Yang Jianfei, Cao Wei, Li Decai, et al. Analysis on zero voltage vector in two-phase conduction direct torque control of brushless DC motor[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4948-4956.

[4] 於鋒, 朱晨光, 吳曉新, 等. 基于矢量分區的永磁同步電機三電平雙矢量模型預測磁鏈控制[J]. 電工技術學報, 2020, 35(10):2130-2140. Yu Feng, Zhu Chenguang, Wu Xiaoxin, et al. Two-vector-based model predictive flux control of three-level based permanent magnet synchronous motor with sector subregion[J]. Transactions of China Electrotechnical Society, 2020, 35(10):2130-2140.

[5] Luo Yixiao, Liu Chunhua. Elimination of harmonic currents using a reference voltage vector based-model predictive control for a six-phase PMSM motor[J]. IEEE Transactions on Power Electronics, 2019, 34(7): 6960-6972.

[6] 李耀華, 秦輝, 蘇錦仕, 等. 永磁同步電機模糊自適應變開關次數權重系數模型預測轉矩控制[J]. 電機與控制學報, 2020, http://kns.cnki.net/kcms/ detail/23.1408.TM20200117.1645.031.html. Li Yaohua, Qin Hui, Su Jinshi, et al. Model predictive torque control of permanent magnet synchronous motor based on adaptive dynamic weight coefficient using fuzzy control[J]. Electric Machines and Control, 2020, http://kns.cnki.net/kcms/ detail/23.1408. TM20200117. 1645.031.html.

[7] 史婷娜, 楊雨要, 周湛清, 等. 基于二次型價值函數的雙電機轉矩同步系統有限集模型預測控制[J]. 中國電機工程學報, 2019, 39(15): 4531-4541. Shi Tingna, Yang Yuyao, Zhou Zhanqing, et al. FCS-MPC for dual-motor torque synchronization system based on quadratic form cost function[J]. Proceedings of the CSEE, 2019, 39(15): 4531-4541.

[8] Luo Yixiao, Liu Chunhua. A flux constrained predictive control for a six-phase PMSM motor with lower complexity[J]. IEEE Transactions on Industrial Electronics, 2019, 66(7): 5081-5093.

[9] Zhang Yongchang, Yang Haitao. Model-predictive flux control of induction motor drives with switching instant optimization[J]. IEEE Transactions on Energy Conversion, 2015, 30(3): 1113-1122.

[10] 徐艷平, 李園園, 張保程, 等. 一種消除權重系數三矢量模型預測轉矩控制[J]. 電工技術學報, 2018, 33(16): 3925-3934. Xu Yanping, Li Yuanyuan, Zhang Baocheng, et al. Three-vector based model predictive torque control of eliminating weighting factor[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3925-3934.

[11] 張永昌, 楊海濤, 魏香龍. 基于快速矢量選擇的永磁同步電機模型預測控制[J]. 電工技術學報, 2016, 31(6): 66-73. Zhang Yongchang, Yang Haitao, Wei Xianglong. Model predictive control of permanent magnet synchronous motors based on fast vector selection[J]. Transactions of China Electrotechnical Society, 2016, 31(6): 66-73.

[12] 周揚忠, 程明, 熊先云. 具有零序電流自矯正的六相永磁同步電機直接轉矩控制[J]. 中國電機工程學報，2015, 35(10): 2504-2512. Zhou Yangzhong, Cheng Ming, Xiong Xianyun. Direct torque control for six-phase permanent magnet synchronous motor with zero-sequence current self-adjust[J]. Proceedings of the CSEE, 2015, 35(10): 2504-2512.

[13] Gonzalez-Prieto I, Duran M J, Aciego J J, et al. Model predictive control of six-phase induction motor drives using virtual voltage vectors[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 27-37.

[14] 徐質閑, 王政, 王學慶, 等. T型三電平雙三相永磁同步電機驅動零共模電壓模型預測控制[J]. 中國電機工程學報, 2020, 40(13): 4301-4310. Xu Zhixian, Wang Zheng, Wang Xueqing, et al. A predictive current control method for a T-type three-level dual three-phase PMSM with zero common-mode voltage[J]. Proceedings of the CSEE, 2020, 40(13): 4301-4310.

[15] 夏長亮, 仇旭東, 王志強, 等. 基于矢量作用時間的新型預測轉矩控制[J]. 中國電機工程學報, 2016, 36(11): 3045-3053. Xia Changliang, Qiu Xudong, Wang Zhiqiang, et al. Predictive torque control based on optimal operating time of vector[J]. Proceedings of the CSEE, 2016, 36(11): 3045-3053.

[16] Huang Wentao, Hua Wei, Yin Fangbo, et al. Model predictive thrust force control of a linear flux-switching permanent magnet machine with voltage vectors selection and synthesis[J]. IEEE Transactions on Industrial Electronics, 2019, 66(6): 4956-4967.

[17] Lin Xiaogang, Huang Wenxin, Jiang Wen, et al. Deadbeat direct torque and flux control for permanent magnet synchronous motor based on stator flux oriented[J]. IEEE Transactions on Power Electronics, 2020, 35(5): 5078-5092.

Fast Predictive Direct Torque Control of Dual Three-Phase Permanent Magnet Fault Tolerant Machine Based on Weighting Factor Elimination and Finite Control Set optimization

Zhao Yong Huang Wenxin Lin Xiaogang Jiang Wen

（College of Automation Engineering Nanjing University of Aeronautics and Astronautics Nanjing 211106 China）

In this paper, a fast predictive direct torque control (PDTC) based on weighting factor elimination and finite control set optimization is presented. The weighing factors are removed and the number of elements in finite control set are reduced. The heavy computing burden of conventional PDTC for dual three-phase permanent magnet fault tolerant machine system are also released. Firstly, according to the deadbeat direct torque and flux control, the variables with different dimensions in the cost function are all equivalent to the voltage vectors, eliminating the weighting factor of stator flux. Then, based on the large flux leakage of permanent magnet fault tolerant machine, only the voltage vectors or virtual voltage vectors whose zero-sequence voltages are zero are selected as the elements of finite control set. As a result, the weighting factor of zero sequence is eliminated, and the elements number of finite control set is decreased from 64 to 19. Besides that, the zero-sequence currents are improved. Finally, a fast method which just needs one time to select the optimal voltage vector is designed. The experimental results verify the feasibility and effectiveness of proposed PDTC.

Dual three-phase permanent magnet fault tolerant machine, predictive direct torque control (PDTC), weighting factor elimination, optimal finite control set, fast voltage vector selection

TM341

10.19595/j.cnki.1000-6753.tces.200762

國家自然科學基金（51777096）和江蘇省研究生科研創新計劃（KYCX18_0285）資助項目。

2020-06-30

2020-09-10

趙 勇 男，1991年生，博士研究生，研究方向為永磁同步電機及其控制技術。E-mail：zhaoyong1105@nuaa.edu.cn（通信作者）

黃文新 男，1966年生，教授，博士生導師，研究方向為電機及其控制、新型風力發電技術、電能變換、航空電源等。E-mail：huangwx@nuaa.edu.cn

（編輯 郭麗軍）