負載換流逆變器驅動電勵磁同步電機無速度傳感器模型預測控制方法
寇佳寶 高 強 滕詠哮 徐殿國
負載換流逆變器驅動電勵磁同步電機無速度傳感器模型預測控制方法
寇佳寶 高 強 滕詠哮 徐殿國
(哈爾濱工業大學電氣工程及自動化學院 哈爾濱 150001)
負載換流逆變器(LCI)驅動電勵磁同步電機控制系統廣泛應用于中高壓場合,在應對干擾和負載變化上,較大的系統慣性系數和較低的開關頻率導致其動態響應性能欠佳。該文提出一種基于LCI驅動電勵磁同步電機的無速度傳感器模型預測控制方法。首先根據LCI的數學模型建立預測狀態方程,同時給出合適的代價函數和約束條件;然后分析負載換相模式下的控制矢量模型,給出速度觀測器的設計方法和參數選擇依據,并針對負載變化對速度觀測產生的影響進行分析和補償。同時該觀測器還能夠同時實現逆變橋輸入電壓和端電壓相位的觀測;最后,通過3.75kW的LCI驅動電勵磁同步電機實驗平臺對提出的無速度傳感器模型預測控制方法進行實驗驗證。結果表明所提出的控制方法能夠有效提升系統的動態響應性能,所設計的觀測器具有可行性,速度觀測結果在額定階躍負載下誤差小于13°。
負載換流逆變器 電勵磁同步電機 無速度傳感器 模型預測控制
0 引言
負載換流逆變器(Load Commutated Inverter, LCI)驅動電勵磁同步電機具有容量大、成本低、可靠性高和控制簡單等特點,因此該驅動系統被廣泛應用于高速精軋機、大型燃氣輪機、抽水蓄能電站及其他風機泵類等中高壓場合[1-4]。在高速精軋機的工況應用中,驅動系統需要在鋼材加入后快速穩定在預定轉速上,這就要求所采用的控制算法在負載快速變化時有著較好的動態響應特性。如果穩定轉速效果不佳,會導致軋制鋼材的堆積和產品加工失敗。而好的動態響應能力能夠有效減小變載時的速度變化,縮短速度恢復時間,從而直接提高成品率和鋼品質量。在大型燃氣輪機、抽水蓄能電站及其他風機泵類工況應用中,更高的動態響應速度能夠使系統更好地應對干擾和負載變化,從而提高機組起動的成功率和系統的穩定性[5]。
模型預測控制由于建模難度低、魯棒性和穩定性較高、動態響應性能好等優勢逐漸開始取代傳統控制方法。但它同時存在穩態波動大、計算量大等問題[6-10]。而LCI驅動電勵磁同步電機系統慣性系數高,這可以抑制模型預測控制帶來的穩態波動問題。由于LCI采用半控型晶閘管器件作為其電力電子器件,因此其控制頻率通常僅為幾百赫茲,不過較低的開關頻率相比其他驅動系統來說,為算法在線運行留出了更充足的計算資源。文獻[10-11]提出了一種基于LCI的模型預測控制方法,該方法采用多級控制,但只有部分采用了模型預測控制,因此所采用的模型預測控制實際應用效果受到了其他控制器的限制。
此外,傳統的機械式傳感器安裝繁瑣,難以保證其安裝同軸度,可靠性也較低。在一些特殊工況下,如高溫易爆和水下場合,甚至無法完成機械式傳感器的安裝。目前無傳感器控制方法已有豐富的研究成果,但大多都集中在永磁同步電機、異步電機及開關磁阻電機等[12-15]。文獻[16]設計了一種基于電勵磁同步電機的速度觀測器,但并未考慮負載變化給觀測帶來的影響。文獻[17]設計了一種速度觀測器,但負載換相模式給速度觀測帶來的影響未被考慮。
本文基于LCI驅動電勵磁同步電機控制系統提出了一種無速度傳感器模型預測控制方法。提出的單級模型預測控制方法能夠避免多級控制帶來的木桶效應,提高系統的動態響應性能,降低硬件成本并提高系統運行的可靠性。本文首先分析了LCI模型,推導了系統的預測狀態方程,并給出相應的代價函數和參數約束。然后分析負載換流模式下的矢量模型,設計了一種適用于高速階段的多參數觀測器并給出了參數選擇依據,同時針對負載換相模式運行特點和負載變化給觀測帶來的影響進行了補償。最后通過3.75kW的LCI驅動電勵磁同步電機實驗平臺對提出的無速度傳感器模型預測控制方法進行了實驗驗證。
1 LCI驅動電勵磁同步電機模型預測控制
1.1 LCI驅動拓撲數學模型
圖1為LCI驅動器拓撲結構。該結構主要包括整流橋、逆變橋及平波電抗器三部分。圖1中rec為整流輸出電壓,inv為逆變輸入電壓,dc為直流母線電流,dc為平波電抗器電感,dc為直流母線等效電阻。

圖1 LCI驅動器拓撲結構
以LCI回路建立等效電壓模型,其表達式為

對于其中的三相全控整流橋來說,其輸出電壓與網側電壓的數學關系為

式中,s為網側相電壓有效值;為整流橋的觸發延遲角。
在LCI驅動器中,整流橋與逆變橋具有完全相同的拓撲結構,僅有能量流向相反。在控制策略上,整流和逆變通過改變觸發延遲角即可實現相互切換。為了實現與整流橋相反的能量流向,逆變橋的觸發延遲角需要大于90°。因此,逆變輸入電壓數學表達式可表示為
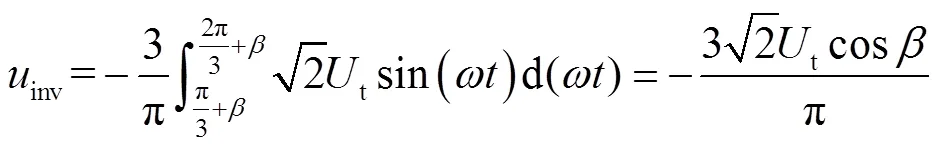
將式(2)和式(3)代入式(1)中,則LCI回路電壓方程可表示為
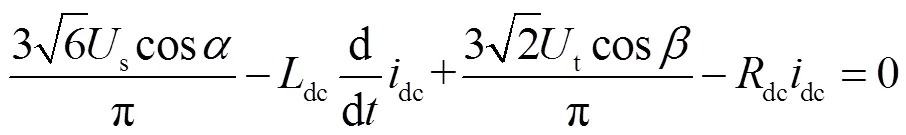
電機的機械運動方程為

式中,e為電機的電磁轉矩;L為負載轉矩;為軸系轉動慣量;為粘滯系數;r為轉子的機械轉速。
忽略逆變橋的能量損耗,電機的電磁轉矩可以表示為
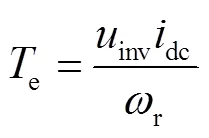
當電勵磁同步電機采用恒勵磁電流控制時,uinv/idc可近似為定值。將式(6)代入式(5)中,電機的機械運動可表示為

