地下物流系統網絡數學模型構建

王玉學, 汪子強

(東北石油大學數學與統計學院，大慶 163318)

1 引言

交通擁堵是許多國際城市都遇到的“困局”之一.世界各國都在為解決城市交通問題進行積極探索，城市交通擁堵的主要原因是地面道路上車輛、車次數量巨增.因此，統籌規劃地下空間開發勢在必行，地下物流系統(ULS)正受到越來越多的關注和重視.現代地下物流系統的研究已近30 年，但系統復雜、修建成本高，且尚無系統的理論和實驗支持實際應用，因此，目前沒有一個成功的案例可供借鑒研究.

國際上關于ULS 的研究主要集中在概念研究、可行性研究、網絡模型構建及優化和仿真研究.在技術方面，Berner 等[1]提出以電磁為動力的地下物流系統和真空貨物倉地下物流系統，并進行了模型試驗.但考慮成本及工程等現實因素，這些模型還無法應用于現實.Vleugel 和BAL[2]考慮用新型的共享交通工具取代地上占用空間及資源的運輸工具，并建立獨立的交通網絡，以緩解運輸壓力.在ULS 模型建立和研究方面，包括模擬植物生長算法、遺傳算法和數值分析等方法研究.Bashiri 等[3]對樞紐選址問題進行建模，提出用遺傳算法、參數整定和模擬退火算法求解模型，并給出了合適的求解算法.

2004 年，錢七虎院士在國內首次明確提出ULS 可以為解決城市交通擁堵問題提供新思路，并以北京為研究對象展開研究.學者研究建立的ULS 模型包括0-1 選址模型、規劃模型等，隨著數據挖掘算法的發展和應用，機器學習、粒子群算法等也應用其中[4].我國城市和物流業發展迅速，亟需對地下物流系統的研究和實踐應用進行探索以緩解交通壓力，目前我國地下工程的技術水平發展迅速，基本滿足系統建設條件，相關研究已具備現實意義和可應用性.本文根據收集到的資料和南京市仙林區的實際情況，首先建立該區域節點選擇模型，確定該區域地下物流網絡節點群，一級節點與物流園區相連并可跨區域調運貨物，二級節點與非本區域一級節點僅通過本區域一級節點連通.在確定節點群的基礎上選擇合適的地下路線，建立該區域的ULS 網絡.在滿足該市交通需求(假定需求量每年以穩定速度增長)的前提下，給出該區域網絡路線的以八年為期限的建設時序及演進圖.

2 確定ULS 節點群

在建立模型前，根據實際情況做出以下假設：

假設1 物園區到一級節點采用雙向四軌軌道；一級節點和二級節點之間、一級節點和一級節點之間采用雙向雙軌軌道.

假設2 四個物流園從地面收發貨物總量上限為4000 噸，進出4 個物流園區的貨物放入地下運輸.

假設3 交通擁堵指數取值范圍為0-10，“0-2 暢通”、“2-4 基本暢通”、“4-6 輕度擁堵”、“6-8 中度擁堵”、“8-10 嚴重擁堵”，數值越高，交通擁堵越嚴重.

假設4 所有節點的服務半徑為3 公里，節點間距離不受限制.

假設5 運輸車由八節車輛構成；載重為10 噸；運行速度13.5 米/秒；加速度1米/秒2；每個節點每小時發車5班，每天運營18 小時.

根據各區域的中心點坐標，將一級節點及二級節點的位置確定為區域的中心點，中心點在節點的服務半徑內即視為節點對該區域進行了覆蓋.對收集的資料中的OD 流量矩陣、中心點坐標及各區域交通擁堵系數進行分析，改進鮑摩-瓦爾夫模型建立單目標優化模型，再確定二級節點的數目及位置.根據計算結果篩選出主次一級節點和主次二級節點的個數并確定位置.

經過各種模型的對比，本文以集合覆蓋模型來解決一級節點、二級節點選址的計算，集合覆蓋模型的基本思想是以最少數量的節點、最大的服務半徑覆蓋所有區域的中心點[5].考慮到緩解交通擁堵及成本問題，本文構建一個目標函數：

式中：T 表示各區域中心點總貨物中轉量，單位：噸；α 表示該節點所代表區域的平均擁擠系數；L 表示節點到物流園區的距離長度，單位：米.

當某區域貨運量大、擁擠程度高且距離物流園區近時，優先考慮作為一級節點，為此將函數值F(x)作為評判一級節點與二級節點的指標.根據所收集資料的貨運OD 流量矩陣，計算各區域總貨物輸出量和輸入量，得到總貨物周轉量.并根據交通擁堵指數和計算得到的總貨物周轉量，建立回歸模型.通過歐式距離公式，計算得到各點到其他所有點的距離矩陣.統計編號為1、2、3、4 物流園區及編號為791-900 區域對除本身外所有物流園區及區域的接收量總和與發出量總和.數據處理和計算通過Matlab 編程實現.

具體的計算與分析過程如下：

1) 雙向四軌道線路單向最大貨運量：10×8×5×18×2=14400 噸；

2) 由于限制條件一級節點與物流園區相連，若一、二、三物流園區分別只與一個一級節點相連，則可得一、二、三物流園區一天最大單向貨運量：14400+4000 =18400 噸；

3) 由于18400 噸均小于一、二、三物流園區的最大單向貨運量，則會出現每天貨物滯留情況，所以對一、二、三物流園區分別至少要與兩個一級節點相連；

4) 考慮到成本問題，一、二、三物流園區分別與兩個一級節點相連；對于兩個一級節點，函數值大的定義為主一級節點、函數值小的定義為次一級節點；四物流園區一個一級節點即可滿足單向最大貨運量；

5) 綜上計算確定一級節點為7 個，二級節點為C[k]中節點數減去一級節點數.

模型求解：

1) 以每個區域中心點作為中心，以3 公里為服務半徑，令i 表示非物流園區區域的編號，P(i)表示每個中心服務范圍內被服務過的區域中心點的個數，A[i]表示每個中心服務范圍內被服務過的區域中心點編號的集合，篩選出最大的P(i)值，并記錄相應的i 值及其對應的區域編號，以此區域編號作為一個節點，并記錄于C[k]中；

2) 在編號為791-900 區域中除去A[i]中的區域，在剩余的區域中心點中重復第一步，直至篩選出所有的節點，并滿足以這些節點為中心，以3 公里為服務半徑，能夠將編號791-900 區域的所有區域中心點進行覆蓋；

3) 一物流園區單項最大貨運量19299.37 噸，二物流園區單項最大貨運量18981.112 噸，三物流園區單項最大貨運量18684.818 噸，四物流園區單項最大貨運量8923.678 噸.

經過計算求得一級節點7 個，編號分別為：847、813、825、808、874、894、867；二級節點8 個，編號分別為：857、811、824、864、871、794、887、899.對于未在節點最大服務范圍內的區域：895 和896，通過查閱，區域895 與896 的交通擁擠指數分別為1.33 與3.91，屬于暢通和基本暢通范圍，故不需要緩解區域895 與896 的交通，即不需要對區域895 與896 進行覆蓋.各節點位置與覆蓋區域如圖1 所示.

圖1 各節點位置與覆蓋區域

3 建立ULS 網絡

地下物流網絡節點群選取后，需要選擇合適的地下路線，建立ULS 網絡.鮑摩-瓦爾夫模型不僅考慮了運輸成本，而且還考慮了可變成本和固定成本[6].因此將總成本作為目標函數，擬建立一個考慮多個影響因素且具備一定約束條件的ULS 網絡模型，利用遺傳算法對模型求解[7]，得出隧道的最優網絡構成.

根據實際情況做出假設：相鄰節點以單向流量較大為設計原則；每天總成本由貨物的運輸成本和地下物流隧道與節點的折舊構成；貨物運輸成本固定，為1 元/噸·公里；不考慮物流園區的地下節點建設；一年共360 天.網絡建設總成本費用主要包括固定建設投資成本和運營成本，固定建設投資成本包括供需節點建設成本和地下物流隧道建設總成本.設物園區個數為H，一級節點的總個數為U，二級節點的總個數為I，現定義變量

運輸總成本

地下物流隧道建設總成本

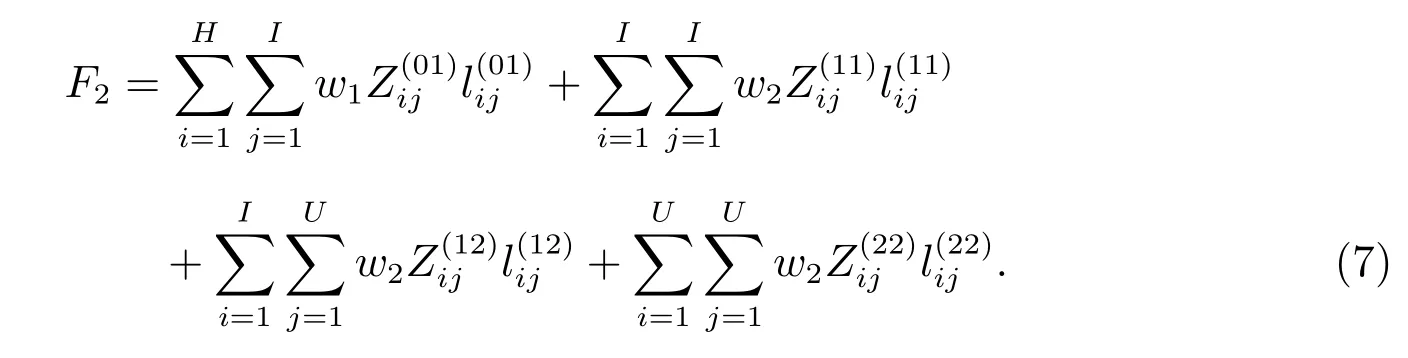
一級、二級節點的建設總成本

綜上所述，可得總成本

由此構建模型

為了對模型求解，假設節點與管道容量有限制，并做出約束條件

式中：A 表示每噸貨每公里的平均運輸成本，億元；Wij表示各個供需點之間每公里的軌道建設成本，億元；qij表示各個供需點之間的貨運量，噸；lij表示各個供需點之間的路線距離，米；c1表示一級節點建設成本，億元/個；c2表示二級節點建設成本，億元/個；x 表示年綜合折舊率，%；Qmax表示最大節點容量，噸；Gmax表示最大管道容量，噸；Lmax表示最大路線總路程，米.

該模型是一個非確定多項式問題，采用精確算法將無法在可接受的時間內計算出全局最優解.遺傳算法具有很好的收斂性，是一種相同計算精度下計算時間較少的全局優化算法[8].因此，選用遺傳算法求解模型.

圖2 求解目標函數的最優路線

4 ULS 各線路的建設時序及演進過程

通過分析，利用模糊聚類算法[9]將節點聚類，FCM 聚類算法的迭代過程就是希望找到使目標函數達到最小的隸屬度矩陣和聚類中心.根據各類包含區域的平均擁堵指數劃定建立的優先次序及隧道連接，并利用Matlab 進行編程繪圖[10].

根據模型求解出管道線建設方案，如圖3 至圖10.

5 總結

本文對現有物流網絡存在的網絡形態進行了系統的分析，構建了一個可行的城市地下物流網絡系統，建立了一類城市地下物流網絡數學模型.利用集合覆蓋法、遺傳算法、粒子群算法、模糊C 均值算法，求解輸出結果，驗證了模型的正確性和實用性.并且根據提供的數據結合多種實際情況進行逐步優化，使得模型更加準確并接近實際情況.

在模型求解過程中，本文沒有全面考慮每個節點的服務半徑合理情況，而是假設大部分服務半徑為3 千米，忽略了貨物從二級節點至地面后采用人力等在節點服務區域內進行運輸的成本，使得模型準確性有一定偏差.在ULS 各線路的建設時序及演進過程求解過程中沒有使用權重計算方法，只選擇模糊聚類算法，并不能完美解釋路線建設方案.

在ULS 投入實際建設運營后，影響因素還有很多，如政策影響、投入力度和環境污染等，另外本文沒有考慮到地鐵運輸情況是否會與地下物流運輸通道產生沖突.本文的運輸網呈現樹型結構，并環形網絡到達點有一定困難.故在選擇算法上只能選用傳統的遺傳算法和粒子算法，沒有采用蟻群算法.對于之后加入其它影響因子的同時，可以使用主成分分析法討論影響因子重要性問題，同時在數據不斷增大的同時配合聚類分析方法和重心法能夠找到更準確的中心點，考慮更加全面.

圖3 第一年管道建設

圖4 第二年管道建設

圖5 第三年管道建設

圖6 第四年管道建設

圖7 第五年管道建設

圖8 第六年管道建設

圖9 第七年管道建設

圖10 第八年管道建設