帶有死亡和意外返還條款的DC 型養老金的最優投資問題

陳佳辰, 榮喜民, 趙 慧

(天津大學數學學院，天津 300354)

1 引言

上世紀50 年代，Markowitz[1]提出的資產選擇理論認為投資的分散化有利于消除非系統性投資風險.保險基金的規模巨大，其安全性直接關系到被保險人利益和社會穩定，因此應該考慮采用組合投資的方式進行風險分散，來消除非系統風險.以Sharpe[2]、Lintner[3]和Mossin[4]為代表的經濟學家從實證出發，探索Markowitz 理論在現實實踐的簡化，從而產生了資本資產定價模型.該模型描述了投資者采用Markowitz理論進行投資管理的條件下，市場價格均衡狀態的形成，實現了證券理論從定性分析到定量分析的轉變，成為研究證券市場中資產的預期收益率與風險之間關系的基本模型.其中Sharpe[2]給出的資本資產定價模型，提供了一種衡量風險價值的方法，可以幫助投資者判斷風險與投資收益是否匹配.榮喜民等[5]提出的組合證券投資最優化模型在一定程度上克服了Markowitz 理論的不足.

養老保險是一種重要的社會保險，有兩種不同的設計方式，一種是DB 型，另一種是DC 型.在DB 型養老金中，每期的給付額是在繳費前確定的，是依據被保險人的最終工資水平以及工作年限計算得到，而繳費率是在估值過程調整得到的.而在DC 型養老金計劃中，每期的繳費率是在繳費前確定的，而積累過程中每期的給付額是依靠繳費率和保險基金投資的收益計算得出的，投資過程的風險是由投保人承擔[6].在DC 型養老金計劃的最優投資策略的研究中，現在一般有兩種方式，一種是期望效用最大化，另一種是以均值-方差為目標.Boulier 等[7]、Cairns 等[8]在冪效用函數下考慮了DC 型養老金計劃的最優投資問題；Xiao 等[9]在對數效用函數下分析了DC 型養老金計劃的最優投資問題；Devolder 等[10]、Battocchio 和Menoncin[11]在指數效用函數下研究了DC 型養老金計劃的最優投資問題.Markowitz[1]在1952 年提出了單期離散時間的均值-方差模型；Zhou 和Li[12]得到連續時間的均值-方差模型；Li 和Ng[13]利用隨機控制理論改良模型，將單期離散時間模型推廣到了多期.H?jgaard 和Vigna[14]在均值-方差模型下研究了DC 型養老金的最優投資問題.

He 和Liang[15]研究了一種帶有退還保費條款的DC 型養老金計劃的最優投資策略.而這種有返還條款計劃強調了被保險人在保險有效期內死亡，保費退還給其繼承人的條款.因其涉及死亡退出，所以對本文研究的帶有死亡和傷殘返還的養老金計劃有借鑒意義.研究帶有返還條款的文章還有柴忠芃等[16]、Bian 等[17]以及Li 等[18]等.本論文將依據被保險人壽命的不確定性，借鑒有返還條款的養老保險最優投資策略的相關研究，探討帶有死亡和傷殘返還的養老保險投資問題，通過建立養老金及其風險投資的財富過程，應用隨機最優控制理論，得到相應的Hamilton-Jacobi-Bellman(HJB)方程.通過設解和分離變量等方法求解得到最優投資策略.所得基金投資的最優策略，可為保險公司提供有價值的決策依據.

本文共分五節，其中第2 節和第3 節為本文的核心部分：第1 節為文獻綜述，介紹國內外DC 型養老金相關問題的研究進展，對本文研究思路以及文章結構進行了概括.第2 節建立了數理模型，包括金融市場以及養老金的財富過程.第3 節運用動態規劃方法得到相關的HJB 方程，求解投資問題的最優投資策略以及有效邊界.第4 節分析各個參數對價值函數和有效邊界的影響.第5 節是文章的總結，概括了本文的創新點，提出了本文模型的局限性及日后可以改進提升之處.

2 數理模型

本節將引入金融市場模型以及帶有返還條款的養老金模型，并給出相應養老金計劃的財富過程.

假定市場上有兩種資產供保險人選擇，即一種風險資產和一種無風險資產.定義t 時刻無風險資產的價格為S0(t)，其滿足如下微分方程

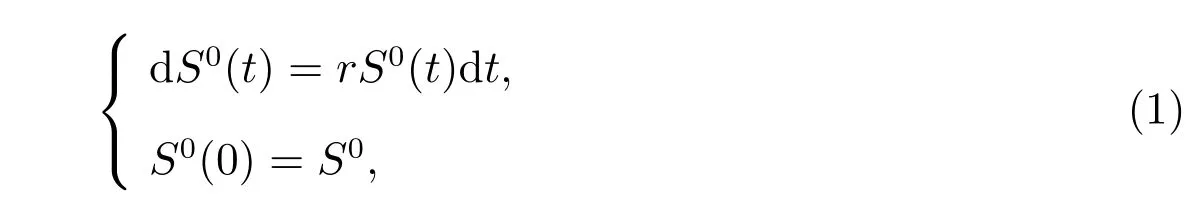
其中r >0 為無風險資產利率.

定義風險資產的價格過程為S1(t)，假設其服從幾何布朗運動，即滿足以下微分方程

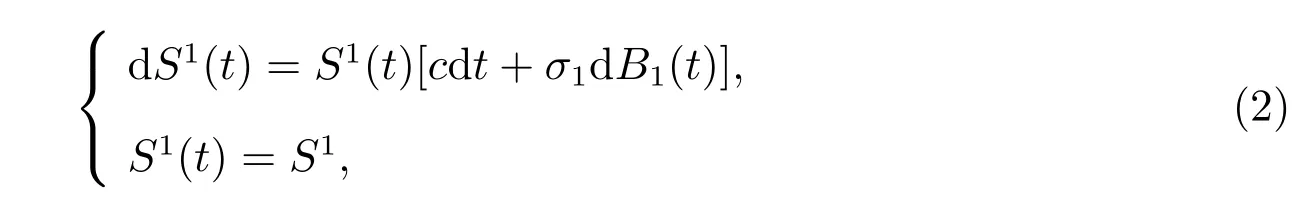
其中c 和σ 分別為風險資產收益率和波動率，都為正常數.B1(t)為概率空間(?,F,P)上的一個標準布朗運動.

在本文中，我們研究養老金計劃在積累過程中的最優投資策略.在養老金計劃中，被保險人會在積累過程中投入一個確定的保費P，其中這個保費是提前確定好的，每期都不會發生改變.被保險人在投保階段內將一直持續投入保費，積累過程將在此過程中一直持續.假設積累過程從ω0歲開始持續到ω0+T 歲，即養老金計劃的時間長度為T.在這個過程中，基金管理者將會把養老金投資在股票和債券上進行保值增值，其中一部分π 將會分配在股票上，剩余部分1 ?π 將會分配在債券上，這里的π 是一個可控變量.若被保險人在積累過程中未發生意外，即保險合同中的賠付條款未被執行，他/她將會在積累過程結束后得到養老金的投資收益，這個數目不是提前確定的，它會受到意外發生概率以及養老金的投資收益所影響.在這里，我們假定該意外為被保險人死亡和傷殘事故.若被保險人在積累過程中死亡，按照養老金合同的一般規定，受益人將會獲得一筆事先確定的賠償金；同理，當被保險人發生傷殘事故時，受益人也會獲得相應的賠償.在模型中，我們假設死亡賠償金為M，用?tqω0+t表示從ω0+t 歲到ω0+t+?t 歲的死亡率，這里的?tqω0+t是一個精算符號，表示在ω0+t 時刻存活，但在?t 時間段內死亡的可能性.所以在t 到t+?t 時刻要賠付的保險金數額為M?tqω0+t，賠付后，積累值和賠付值之差將會分配給存活的被保險人的養老金賬戶.而當被保險人生存時，就有可能發生傷殘事故，在本文中，我們假設在t 到t+?t 時間段內，傷殘事故的賠償由一個復合Poisson 過程表示.又因為被保險人依然存活，所以積累值和賠付值之差將不會在存活的被保險人的養老金賬戶上進行分配.

首先，定義傷殘事故的賠償為R(t)，其形式為

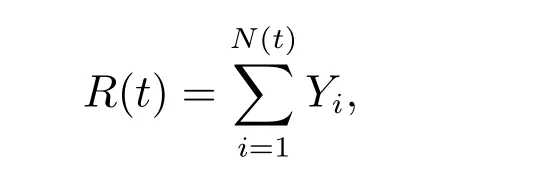
其中N(t)是一個強度為λ 的時間一致泊松過程，表示t 時間段內發生傷殘事故的次數；Yi為均值為η、二階矩為σ22的隨機變量，表示發生傷殘賠償金.

然后，考慮基金規模為X(t)在時間t+?t 時的形式

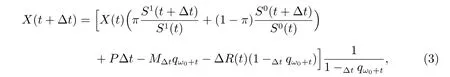
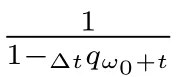
從(3)可以看出，基金規模X(t)會受以下因素影響：投資分配，保險費，死亡率以及積累值與賠付值的差值等.

設

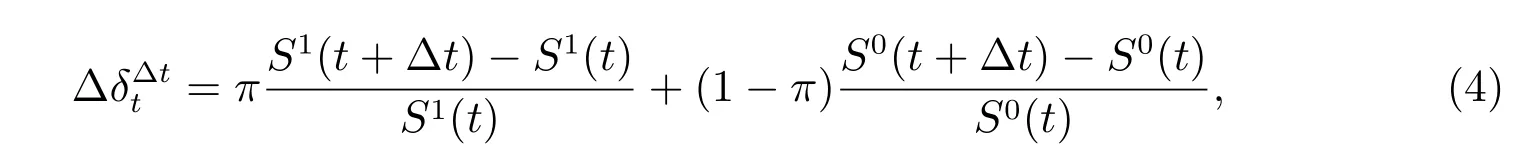
則等式(3)變為

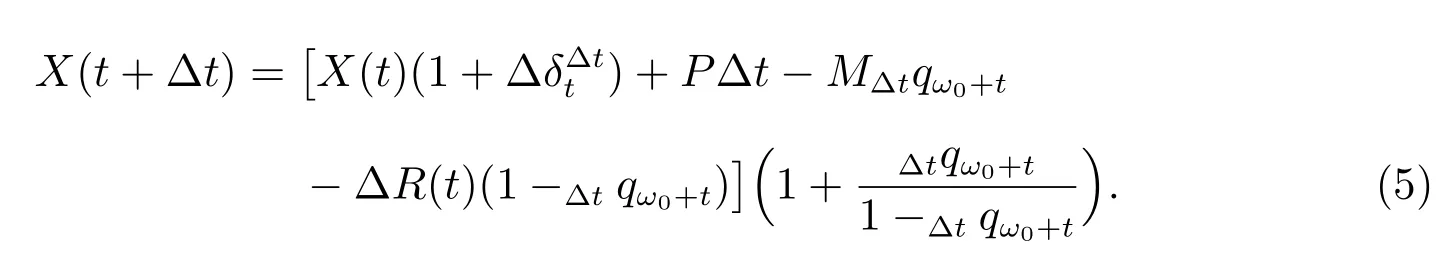
采用精算中的死亡力函數μ(t)來簡化(5)，則條件死亡概率滿足

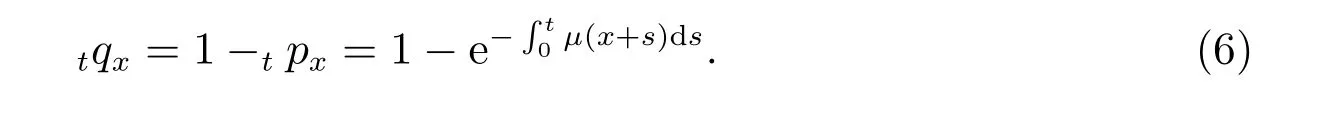
根據上式計算?tqω0+t可以得到

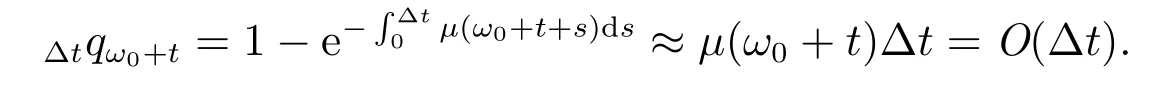
當?t →0 時，μ(ω0+t)在積累過程中的值不大時上式成立，從而可以得到

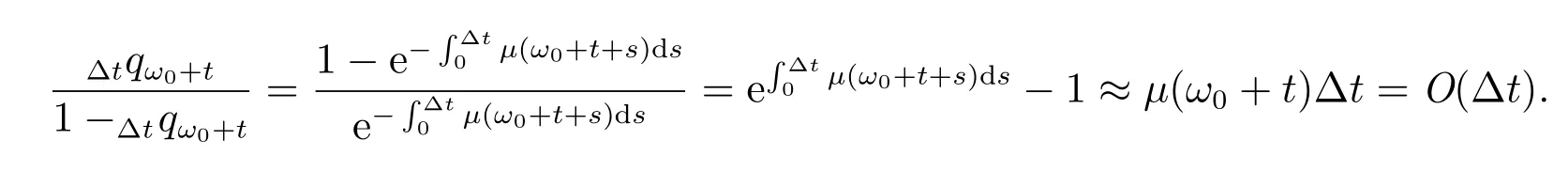
因此可知

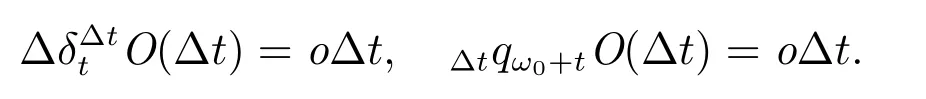
從而等式(5)化為

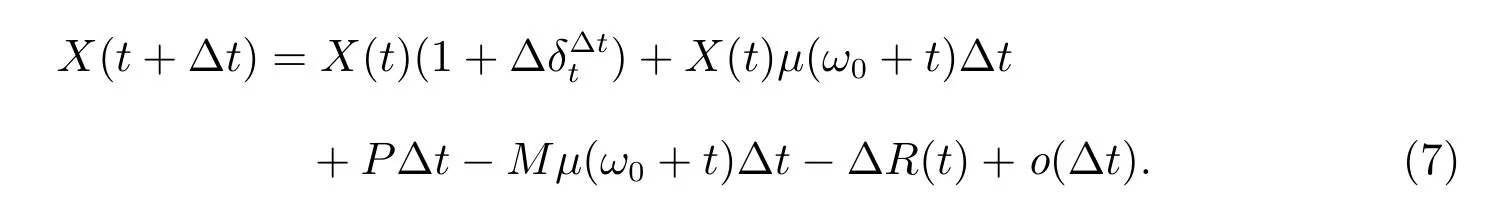
根據?δ?tt 和?R(t)的定義，當?t →0 時，有

因此，基金規模X(t)可以表示為如下連續時間隨機微分方程

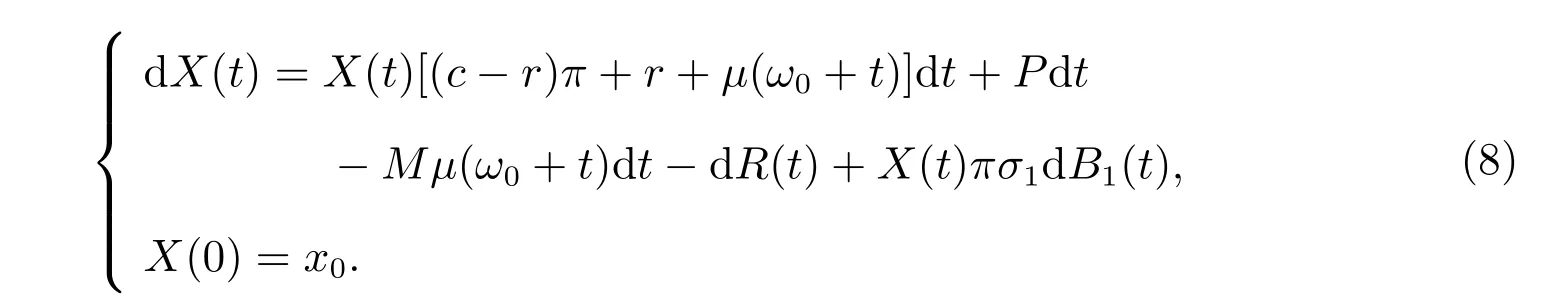
為了簡化模型，我們引入Abraham De Moivre 模型[19]來描述死亡力函數μ(t).在這個模型中，生存函數s(t)和死亡力μ(t)有以下形式

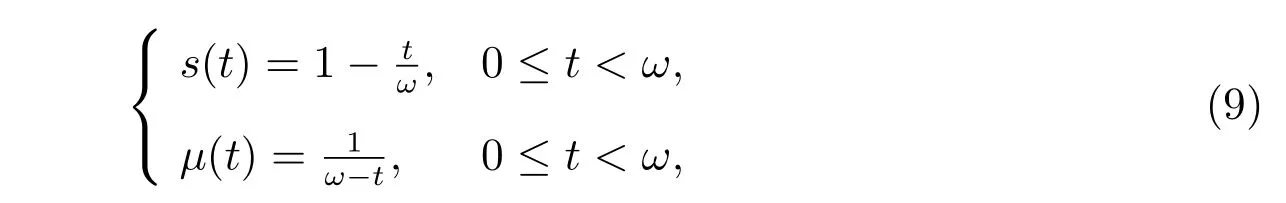
其中ω 是生命年表的最大值，則隨機微分方程有以下形式

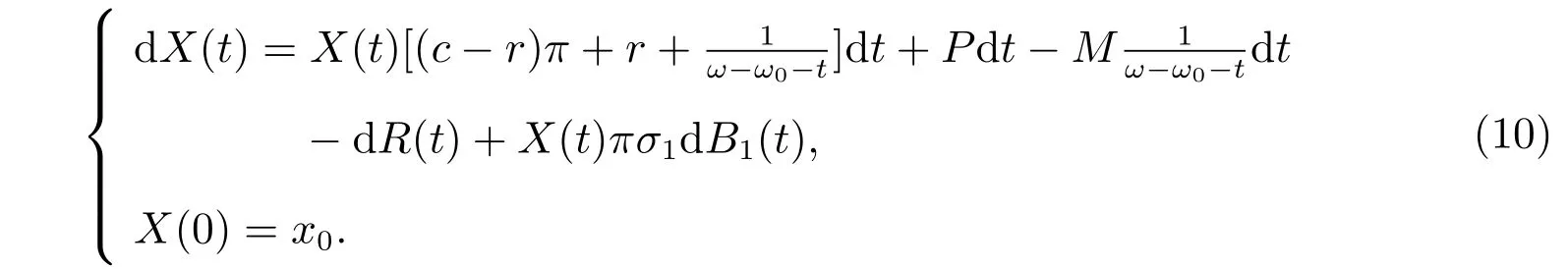
根據文獻[20-22]，我們對復合泊松過程進行近似

其中B2(t)為概率空間(?,F,P)上的一個標準布朗運動，與B1(t)的相關系數為ρ.代入(10)中，可得

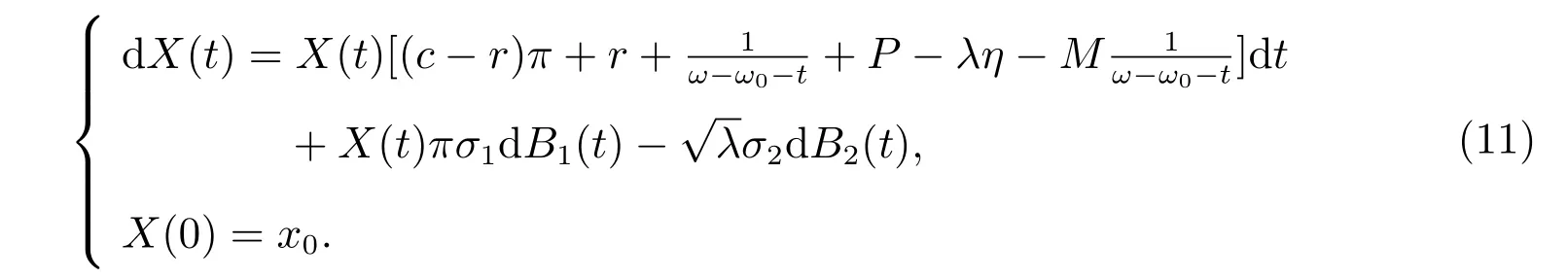
因此，保險賬戶的基金累計值可以被一個根據保險精算規則建立的連續時間隨機過程描述.從積累過程結束后保險人的角度看，保險公司希望可以使基金規模X(t)最大化，并且X(t)的波動最小化.本文選擇均值-方差作為評價準則，則問題可以化為養老金連續時間優化控制問題.基金經理可以選擇最優投資策略，即在股票和債券上分配投資來滿足保險人的目標要求.該優化問題可以描述為

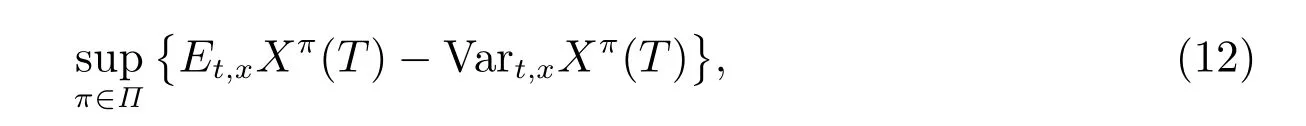
這里的Π ={π|π ∈[0,∞)}是投資策略的集合.

3 最優投資問題求解

在這部分中，我們將求解優化問題(12)，優化分配在股票和債券上的比例，求出有效邊界的形式.首先，利用Bjork 和Murgoci[23]的方法將(12)等價轉化為下面的帶價值函數的時間不一致優化控制問題

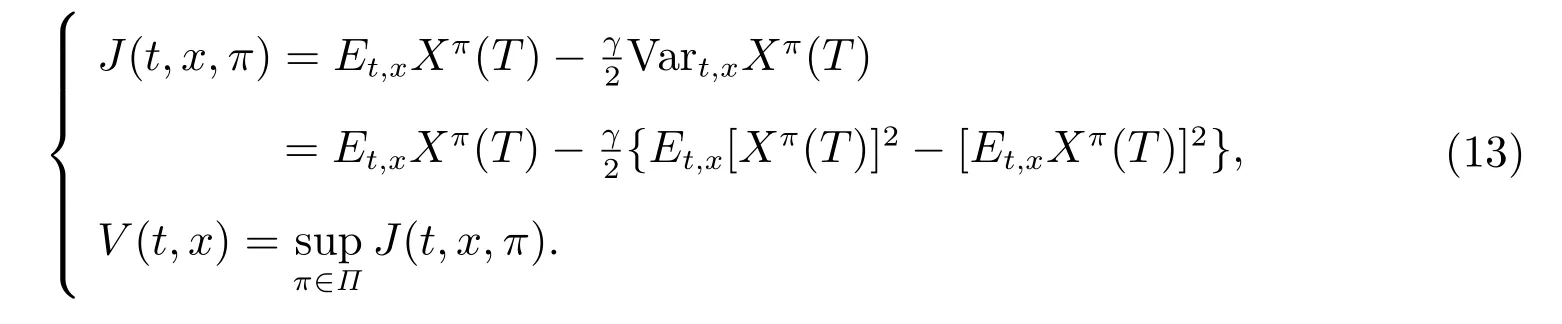
最優投資策略π?滿足V(t,x)=J(t,x,π?).這里γ 是一個正常數，代表的是Vart,xXπ(T)的風險厭惡系數，即通過它描述被保險人的風險厭惡程度.在這里，γ 同時作為一個參量，代表被保險人有不同的風險厭惡程度，會影響投資策略的策略的選擇.

假設

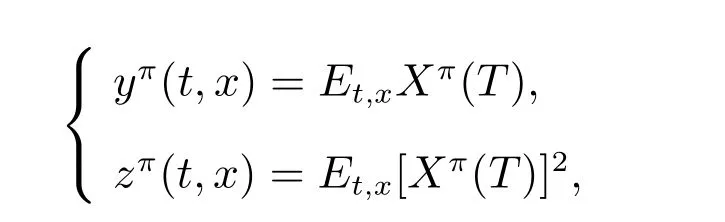
則價值函數V(t,x)變為

定理1(驗證定理) 若存在三個實函數F, G, H :[0,T]×R →R 滿足下面的HJB方程

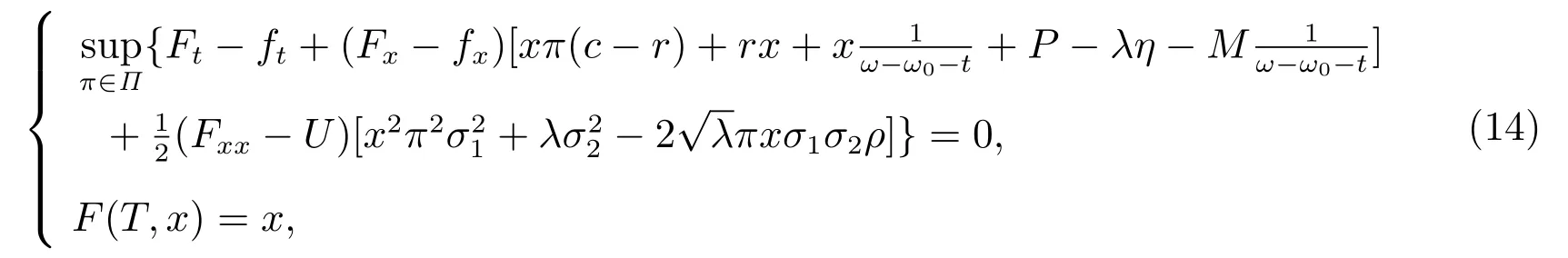
其中

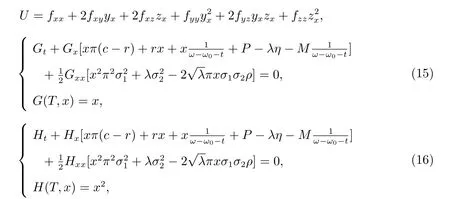
則滿足V(t,x)=F(t,x), yπ?=G(t,x), zπ?=H(t,x)的π?是(13)的最優投資策略.

證明 該定理的證明與文獻[15,24]類似，在這里略去證明.

接下來，我們將求解上述HJB 方程.首先，根據f(t,x,y,z)的形式，可以得到

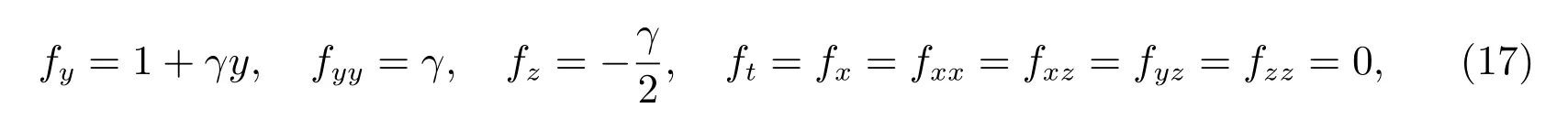
則有

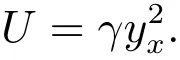
將上式代回(14)，并對π 求微分可得

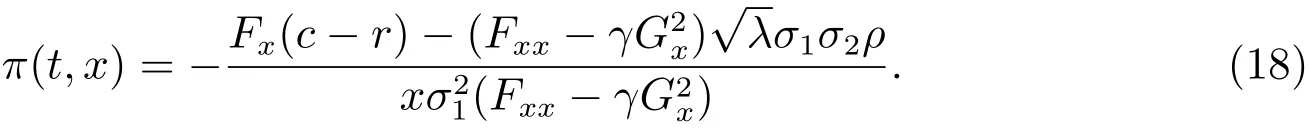
將(18)代回(14)和(15)

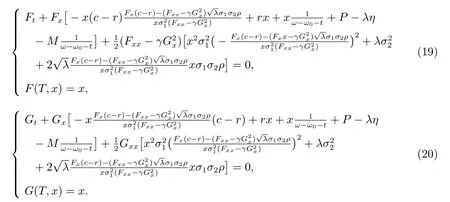
假定F(t,x)和G(t,x)有以下形式

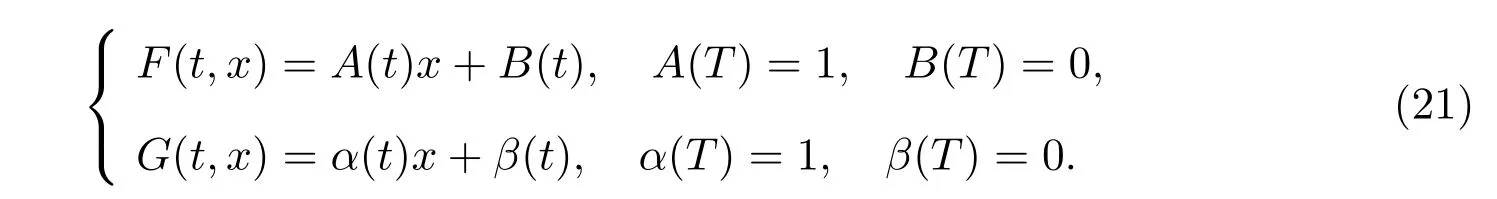
將(21)代回(19)和(20)，可得

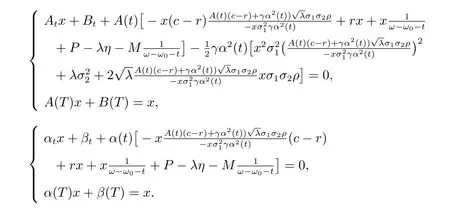
使上面兩個式子中x 的系數和常數項之和為0，則有

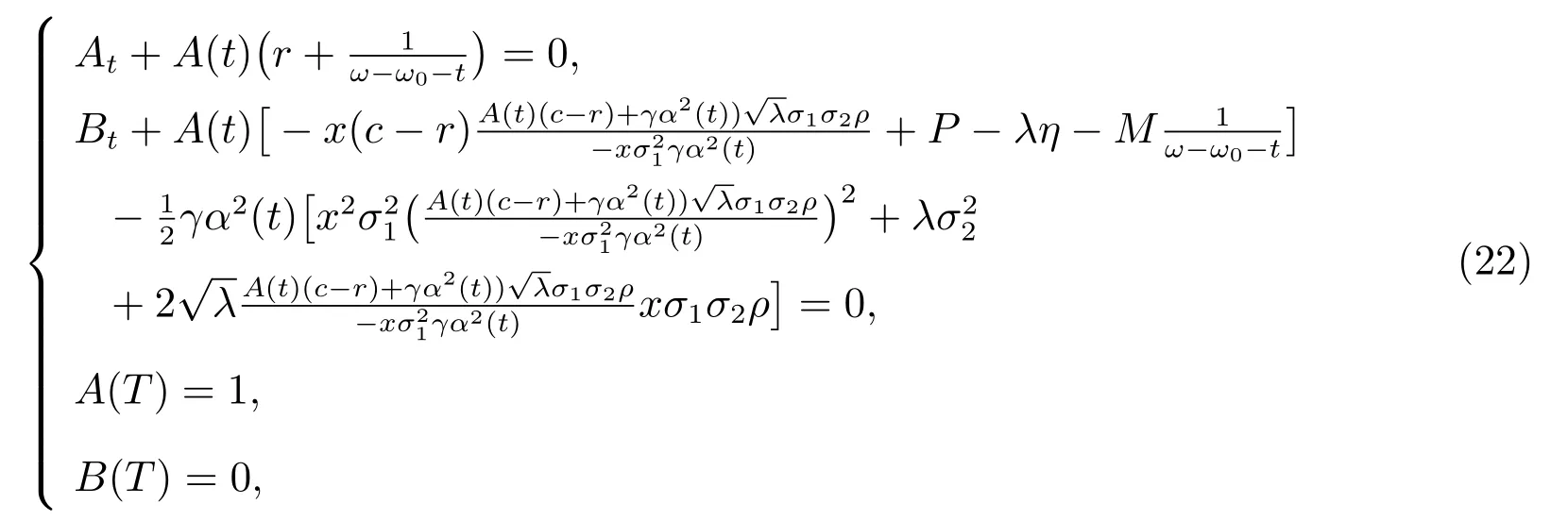
則最優投資策略π?(t)滿足

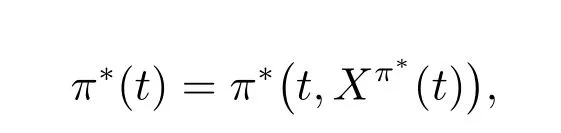
其中Xπ?(t)為隨機微分方程(11)的特解.

顯然，Xπ?(t)是在時間t，最優投資策略π?所對應的最優基金規模.從式(24)可以看出π?是風險厭惡程度γ 的函數.因此，不同的風險厭惡程度的保險人有不同的投資策略，則會產生不同的效用邊界.

接下來給出效用邊界，首先由式(13)，有

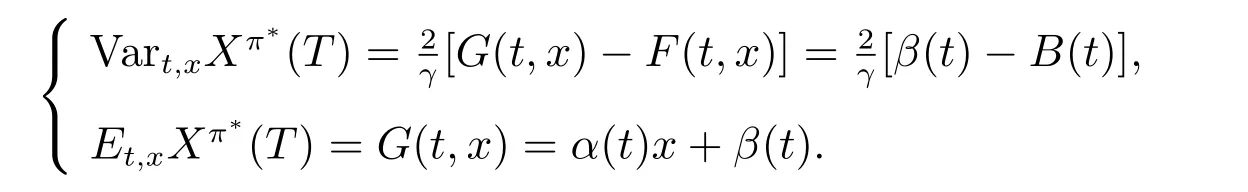
代入α(t), β(t)和B(t)計算可得有效邊界為

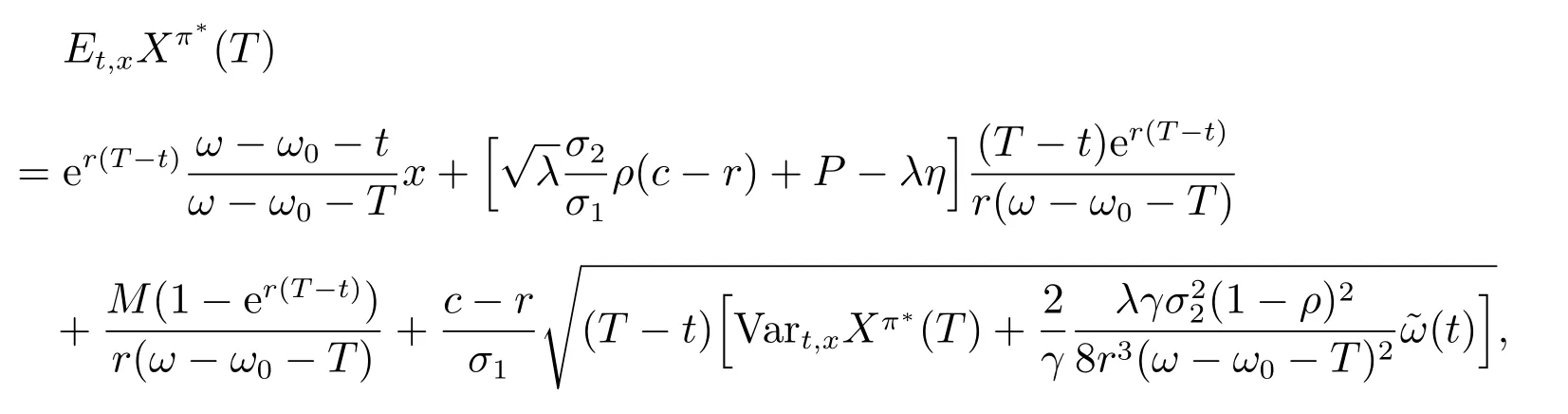
其中

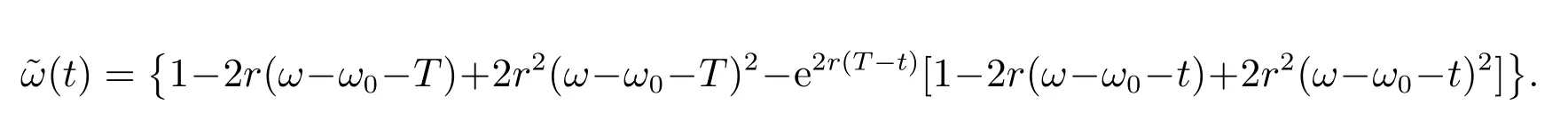
相比于文獻[15]中僅有死亡賠償、沒有傷殘賠償的有效邊界，這里的有效邊界多出了兩項，分別為

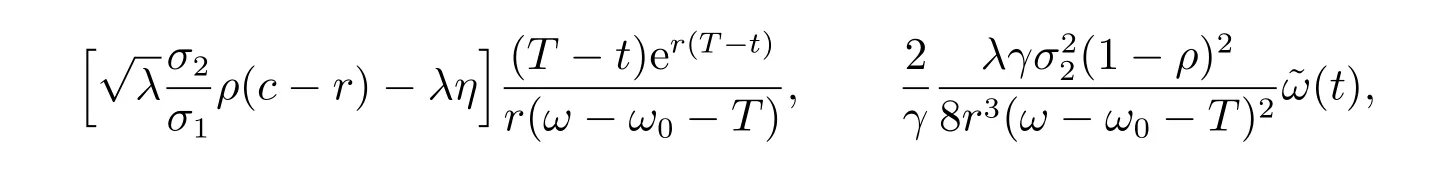
其中第二項在[0,T)內恒小于0，而第一項在通常參數設定下也是小于0 的.這也表明，考慮傷殘賠償后，有效邊界會向下平移，即在承擔相同的風險的情況下，獲得的收益會下降.所以保險公司若要獲得與之前相同的收益，需要承擔更大的風險，將有更多的資金投資于風險資產.

本文假設兩個布朗運動的相關系數ρ ?= 0 是考慮到實際情況中可能存在一些重大的造成傷殘的事故，也會同時影響金融市場.比如：若煤礦發生重大安全事故，在造成人員傷亡的同時，國家可能會進一步加強相關產業的安全監管，要求企業加強安全措施及安全教育，造成企業運營成本增加，從而影響市場對該行業未來盈利能力的信心，導致金融市場出現波動.若確定B1(t)與B2(t)為相互獨立的，可以得到以下推論.

推論1 若布朗運動B1(t)與B2(t)相互獨立，則可以得到DC 型養老金的最優投資策略及有效邊界分別為

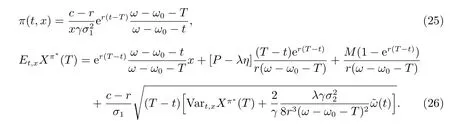
4 數值模擬

在這一節中，將討論各個參數對效用邊界、價值函數以及投資策略的影響.首先，本節中各個參數的默認值如表1 所示.

表1 本節中參數的取值

在第三節中，得到了價值函數V(t,x)的表達式，其形式如下

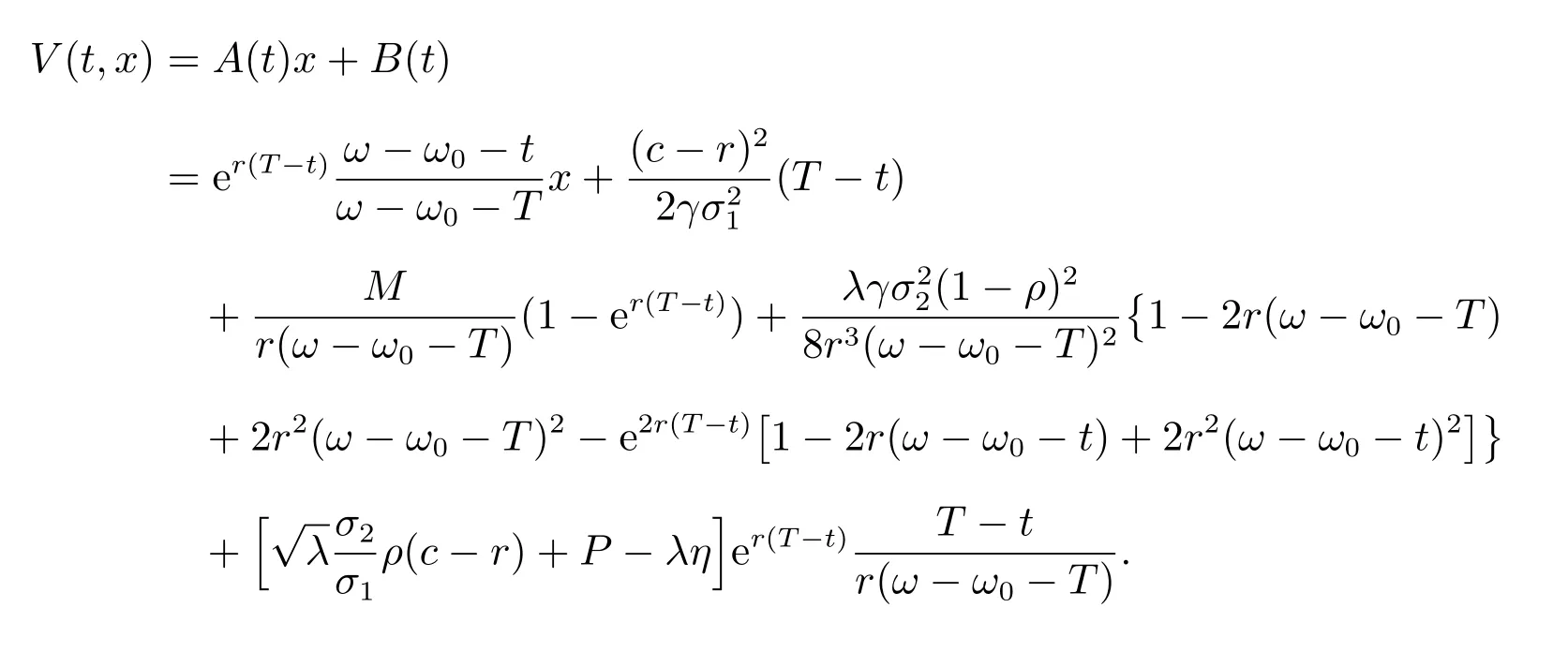
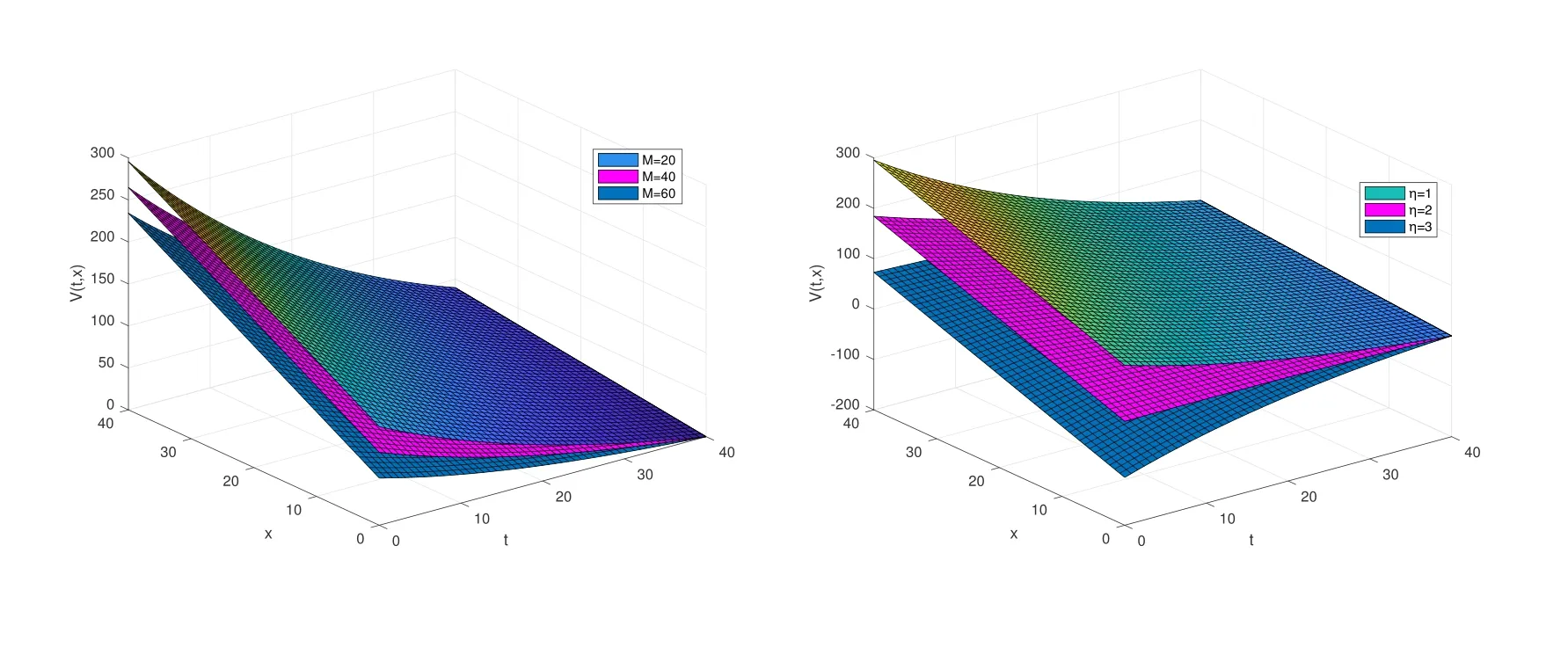
圖1 V(t,x)在不同死亡賠償金M 和傷殘賠償金η 下關于t, x 的變化趨勢

根據該表達式可以得到圖1.從圖1 左圖來看，價值函數的取值關于M 是減函數，這說明提高死亡賠償金，會降低養老金計劃的最終收益，此時保險人為了保證經營管理活動正常進行，應該要提高在風險資產上的投資比例，來獲得更高的投資收益，來保證有足夠的資金來支付給被保險人.同理，從圖1 右圖可以看出，提高傷殘賠償金，也會降低養老金計劃的最終收益，所以應該采取和以上同樣的方法.

從圖2 可以看出，當死亡賠償金和傷殘賠償金上升時，有效邊界會向y 軸下方移動.這就意味著，在承擔相同風險的時候，獲得的收益會下降，在獲得相同收益的時候，承擔的風險會升高.這表明，保險人應采用合理的賠償金，否則過高的賠償金，會增加公司的運營成本，使公司承擔更多的風險.

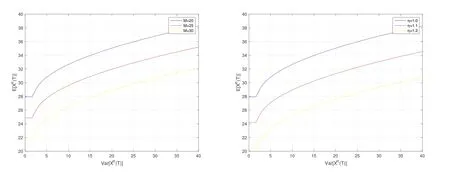
圖2 有效邊界在不同死亡賠償金M 和傷殘賠償金η 下關于t, x 的變化趨勢

5 結論

本文中所用的精算模型是單生命模型，是以概率論為工具，討論個體從生存狀態到死亡狀態的轉換規律的模型.而本文所討論的連續時間投資組合優化問題則是金融數學所研究的核心內容之一，是將金融數學理論運用到實際之中的有效渠道.目前，組合證券投資方法已經被廣泛應用在養老保險投資策略中，相關研究成果很多，He 和Liang[15]考慮了帶有死亡返還的養老保險投資策略，本文的創新點是在考慮死亡返還的同時，加入傷殘返還，是對之前工作的深化.

由于研究工具等方面所限，本文對于保險公司實證研究還沒有深入展開，僅停留在理論階段，而且還存在一些局限性：

1) 在簡化個人的死亡力時，采用了Abraham De Moivre 模型，這個模型提出時間較早，并不能很好的描述實際中的個人壽命，隨著計算機技術的發展，人們可以借助計算機處理更復雜的死亡力函數，所以目前在實務中已經很少使用De Moivre 模型；

2) 本文假設股票價格服從幾何布朗運動模型，很明顯這個模型不能很好的描述金融市場的實際情況，我們可以進一步考慮股票符合其他可以更好描述市場的模型，如CEV 模型、Heston 模型等，來改進本文結果，使其更貼近實際情況.